本記事では、複素積分に関する「コーシーの積分定理」や「留数定理」の実積分への応用の例題一覧を公開しています。
複素関数論の講義の復習、期末試験やレポート、院試対策等に是非お役立てください!
pdfファイルを公開中!

誤りはないように努めておりますが、何かお気づきの点等ございましたら、コメントを頂けますと嬉しいです。
解説動画のある52問!

コーシーの積分定理
問題
- \(\displaystyle \int_0^\infty\cos x^2dx=\frac{1}{2}\sqrt{\frac{\pi}{2}}\), \(\displaystyle \int_0^\infty\sin x^2dx=\frac{1}{2}\sqrt{\frac{\pi}{2}}\)(フレネル積分)
→ 解説動画 #05
- \(\displaystyle \int_0^\infty\frac{\sin x}{x}dx=\frac{\pi}{2}\)(ディリクレ積分)
→ 解説動画 #01
- \(\displaystyle \int_0^\infty\frac{\sin x^2}{x}dx=\frac{\pi}{4}\)
→ 解説動画 #11
- \(\displaystyle \int_0^\infty\frac{\sin x^3}{x}dx=\frac{\pi}{6}\)
→ 解説動画 #25
- \(\displaystyle \int_0^\infty\frac{\sin x^n}{x}dx=\frac{\pi}{2n}\)(\(n=1,2,\cdots\))
→ 解説動画 #36
- \(\displaystyle \int_0^\infty\frac{\sin x^\alpha}{x}dx=\frac{\pi}{2|\alpha|}\)(\(\alpha\neq0\))
→ 解説動画 #47
- \(\displaystyle \int_0^\infty\left(\frac{\sin x}{x}\right)^2dx=\frac{\pi}{2}\)
→ 解説動画 #18
- \(\displaystyle \int_0^\infty\left(\frac{\sin x}{x}\right)^3dx=\frac{3}{8}\pi\)
→ 解説動画 #32
- \(\displaystyle \int_0^\infty\left(\frac{\sin x}{x}\right)^4dx=\frac{\pi}{3}\)
→ 解説動画 #44
- \(\displaystyle \int_{-\infty}^\infty e^{-x^2}\cos(2\beta x)dx=\sqrt{\pi}e^{-\beta^2}\), \(\displaystyle \int_{-\infty}^\infty xe^{-x^2}\sin(2\beta x)dx=\sqrt{\pi}\beta e^{-\beta^2}\)
→ 解説動画 #35
- \(\displaystyle \int_0^\infty \frac{\sin(2\alpha x)}{\sinh x}dx=\frac{\pi}{2}\tanh(\pi\alpha)\), \(\displaystyle \int_0^\infty \frac{x\cos(2\alpha x)}{\sinh x}dx=\frac{\pi^2}{4\cosh^2(\pi\alpha)}\)(\(\alpha\neq0\))
→ 解説動画 #42
留数定理(三角関数)
問題
- \(\displaystyle \int_0^{2\pi}\cos^{2n}\theta d\theta=\frac{{}_{2n}{\rm C}_{n}}{2^{2n-1}}\pi\)(\(n=0,1,\cdots\))
→ 解説動画 #19
- \(\displaystyle \int_0^{2\pi}\sin^{2n}\theta d\theta=\frac{{}_{2n}{\rm C}_{n}}{2^{2n-1}}\pi\)(\(n=0,1,\cdots\))
→ 解説動画 #37
- \(\displaystyle \int_0^{2\pi}\frac{1}{5+3\cos\theta}d\theta=\frac{\pi}{2}\)
→ 解説動画 #02
- \(\displaystyle \int_0^{2\pi}\frac{1}{5-4\cos\theta}d\theta=\frac{2}{3}\pi\)
→ 解説動画 #15
- \(\displaystyle \int_0^{2\pi}\frac{1}{13+5\cos\theta}d\theta=\frac{\pi}{6}\)
→ 解説動画 #26
- \(\displaystyle \int_0^{2\pi}\frac{1}{13-12\cos\theta}d\theta=\frac{2}{5}\pi\)
→ 解説動画 #33
- \(\displaystyle \int_0^{2\pi}\frac{1}{1-2a\cos\theta+a^2}d\theta=\frac{2\pi}{1-a^2}\)(\(|a|<1\))
→ 解説動画 #23
- \(\displaystyle \int_0^{2\pi}\frac{1}{a+b\cos\theta}d\theta=\frac{2\pi}{\sqrt{a^2-b^2}}\)(\(0<|b|<a\))
→ 解説動画 #45
- \(\displaystyle \int_0^{2\pi}\frac{1}{(5+3\cos\theta)^2}d\theta=\frac{5}{32}\pi\)
→ 解説動画 #06
- \(\displaystyle \int_0^{2\pi}\frac{1}{(a+b\cos\theta)^3}d\theta\)\(\displaystyle\ =\frac{2a^2+b^2}{\sqrt{(a^2-b^2)^5}}\pi\)(\(0<|b|<a\))
→ 解説動画 #52
- \(\displaystyle \int_0^{2\pi}\frac{\sin\theta}{1-2a\sin\theta+a^2}d\theta=\frac{2a}{1-a^2}\pi\)(\(|a|<1\))
→ 解説動画 #48
- \(\displaystyle \int_0^{2\pi}\frac{\cos^2\theta}{1-2a\cos\theta+a^2}d\theta=\frac{1+a^2}{1-a^2}\pi\)(\(|a|<1\))
→ 解説動画 #40
- \(\displaystyle \int_0^{2\pi}\frac{\cos2\theta}{2-\sqrt{3}\cos\theta}d\theta=\frac{2}{3}\pi\)
→ 解説動画 #12
- \(\displaystyle \int_0^{2\pi}\frac{\cos3\theta}{5-4\cos\theta}d\theta=\frac{\pi}{12}\)
→ 解説動画 #29
留数定理(有理式)
問題
- \(\displaystyle \int_{-\infty}^\infty\frac{x^2-3x+5}{x^4+13x^2+36}dx=\frac{11}{30}\pi\)
→ 解説動画 #07
- \(\displaystyle \int_{-\infty}^\infty\frac{1}{x^2+a^2}dx=\frac{\pi}{a}\)(\(a>0\))
→ 解説動画 #03
- \(\displaystyle \int_0^\infty\frac{1}{x^3+a^3}dx=\frac{2\sqrt{3}}{9a^2}\pi\)(\(a>0\))
→ 解説動画 #16
- \(\displaystyle \int_0^\infty\frac{1}{x^4+a^4}dx=\frac{\sqrt{2}}{4a^3}\pi\)(\(a>0\))
→ 解説動画 #30
- \(\displaystyle \int_0^\infty\frac{1}{x^6+a^6}dx=\frac{\pi}{3a^5}\)(\(a>0\))
→ 解説動画 #41
- \(\displaystyle \int_0^\infty\frac{1}{x^n+a^n}dx=\frac{\frac{\pi}{n}}{a^{n-1}\sin\frac{\pi}{n}}\)(\(a>0, n=2,3,\cdots\))
→ 解説動画 #49
- \(\displaystyle \int_0^\infty\frac{x}{x^3+a^3}dx=\frac{2\sqrt{3}}{9a}\pi\)(\(a>0\))
→ 解説動画 #20
- \(\displaystyle \int_{-\infty}^\infty\frac{1}{(x^2+a^2)^2}dx=\frac{\pi}{2a^3}\)(\(a>0\))
→ 解説動画 #13
- \(\displaystyle \int_{-\infty}^\infty\frac{1}{(x^2+a^2)^3}dx=\frac{3}{8a^5}\pi\)(\(a>0\))
→ 解説動画 #24
- \(\displaystyle \int_{-\infty}^\infty\frac{1}{(x^2+a^2)^{m+1}}dx\)\(\displaystyle\ =\frac{(2m-1)!!}{(2m)!!}\frac{\pi}{a^{2m+1}}\)(\(a>0, m=0,1,\cdots\))
→ 解説動画 #38
- \(\displaystyle \int_{-\infty}^\infty\frac{x^2}{(x^2+a^2)^3}dx=\frac{\pi}{8a^3}\)(\(a>0\))
→ 解説動画 #34
- \(\displaystyle \int_{-\infty}^\infty\frac{x^4}{(x^2+a^2)^4}dx=\frac{\pi}{16a^3}\)(\(a>0\))
→ 解説動画 #46
留数定理(三角関数×有理式)
問題
- \(\displaystyle \int_{-\infty}^\infty\frac{\cos x}{x^2+1}dx=\frac{\pi}{e}\)
→ 解説動画 #04
- \(\displaystyle \int_0^\infty\frac{\cos x}{x^2+a^2}dx=\frac{\pi}{2a}e^{-a}\)(\(a>0\))
→ 解説動画 #28
- \(\displaystyle \int_0^\infty\frac{x\sin x}{x^2+a^2}dx=\frac{\pi}{2}e^{-a}\)(\(a>0\))
→ 解説動画 #51
- \(\displaystyle \int_0^\infty\frac{x\sin x}{(x^2+a^2)^2}dx=\frac{\pi}{4a}e^{-a}\)(\(a>0\))
→ 解説動画 #21
- \(\displaystyle \int_0^\infty\frac{\cos x\sin x}{x(x^2+a^2)}dx=\frac{\pi}{4a^2}\left(1-e^{-2a}\right)\)(\(a>0\))
→ 解説動画 #14
- \(\displaystyle \int_0^\infty \frac{\sin x}{x\cosh x}dx=\arctan\left(\sinh\frac{\pi}{2}\right)\)
→ 解説動画 #09
留数定理(無理式)
問題
- \(\displaystyle \int_0^\infty\frac{1}{(x+1)\sqrt{x}}dx=\pi\)
→ 解説動画 #08
- \(\displaystyle \int_0^\infty\frac{1}{(x+1)\sqrt[3]{x}}dx=\frac{2\sqrt{3}}{3}\pi\)
→ 解説動画 #17
- \(\displaystyle \int_0^\infty\frac{1}{(x+1)\sqrt[4]{x}}dx=\sqrt{2}\pi\)
→ 解説動画 #27
- \(\displaystyle \int_0^\infty\frac{1}{(x+1)\sqrt[6]{x}}dx=2\pi\)
→ 解説動画 #39
- \(\displaystyle \int_0^\infty\frac{x^{\alpha-1}}{x+1}dx=\frac{\pi}{\sin(\pi\alpha)}\)(\(0<\alpha<1\))
→ 解説動画 #50
留数定理(対数関数)
問題
- \(\displaystyle \int_0^\infty\frac{\log x}{x^2+a^2}dx=\frac{\log a}{2a}\pi\)(\(a>0\))
→ 解説動画 #10
- \(\displaystyle \int_0^\infty\frac{(\log x)^2}{x^2+a^2}dx=\frac{4(\log a)^2+\pi^2}{8a}\pi\)(\(a>0\))
→ 解説動画 #31
- \(\displaystyle \int_0^\infty\frac{\log x}{(x+a)^2}dx=\frac{\log a}{a}\)(\(a>0\))
→ 解説動画 #22
- \(\displaystyle \int_0^\infty\frac{\log x}{(x+a)(x^2+a^2)}dx\)\(\displaystyle\ =\frac{4\log a-\pi}{16a^2}\pi\)(\(a>0\))
→ 解説動画 #43
個別に解説記事も公開中!

上記の再生リスト「今週の実積分」における再生回数の上位5問を個別に解説を行う記事も公開中です。
第一位
第二位
第三位
第四位
第五位
最後に。

コーシーの積分定理や留数定理を学び、実積分の計算に応用できることを知ったとき、とても面白いと感じました。指数関数や対数関数、三角関数が絡んだ(広義)積分が、まさに気持ちよく計算されていきます。
学部時代、複素関数論の講義の試験や院試に向けて、よく演習していました。その経験を活かして、これらのすごさや面白さ、求め方をわかりやすく伝えられればと思っています。是非、動画や記事を参考に、試行錯誤してみてください。
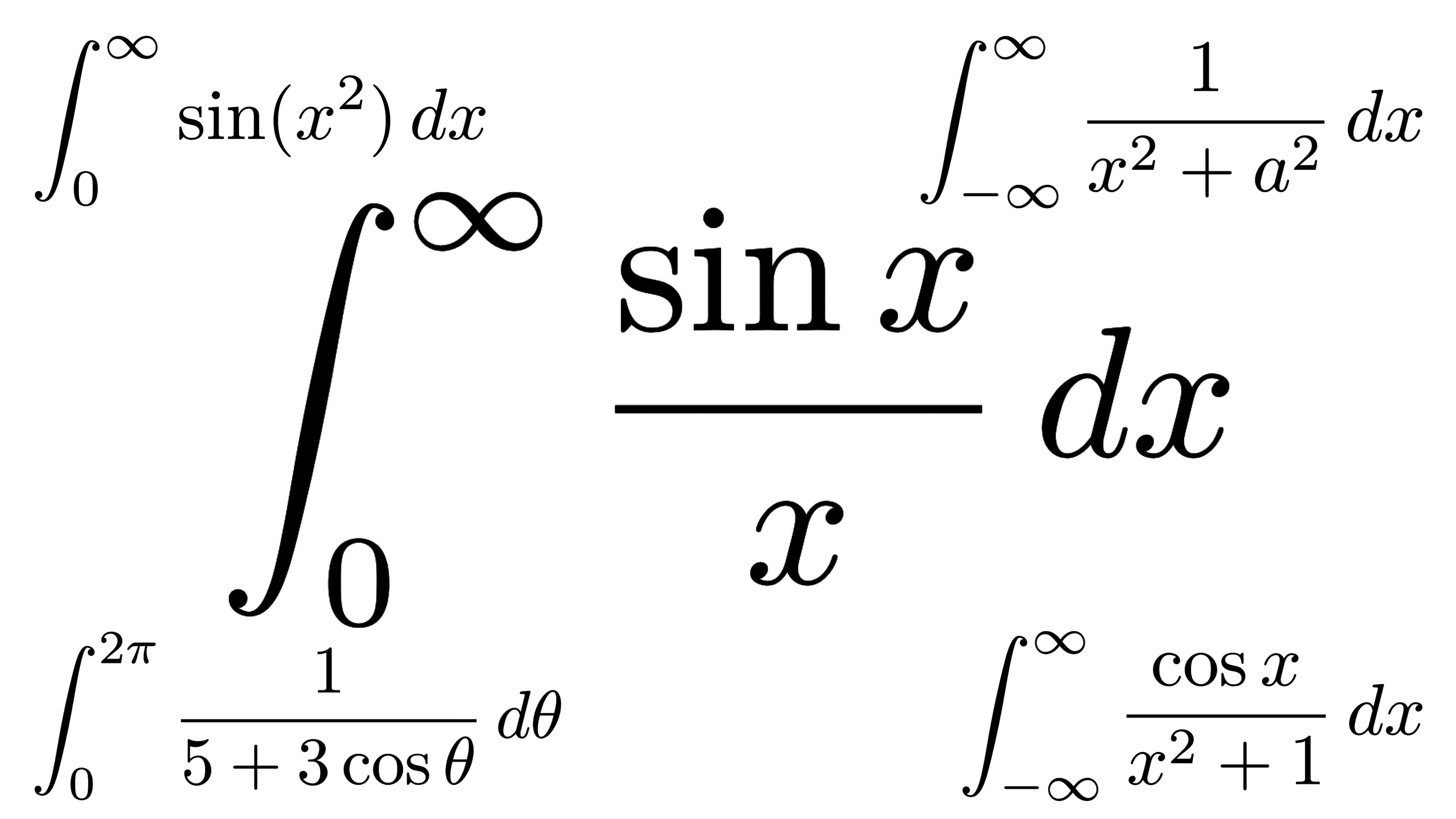


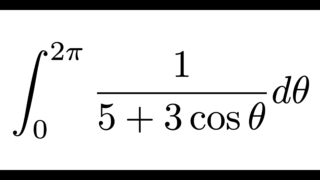


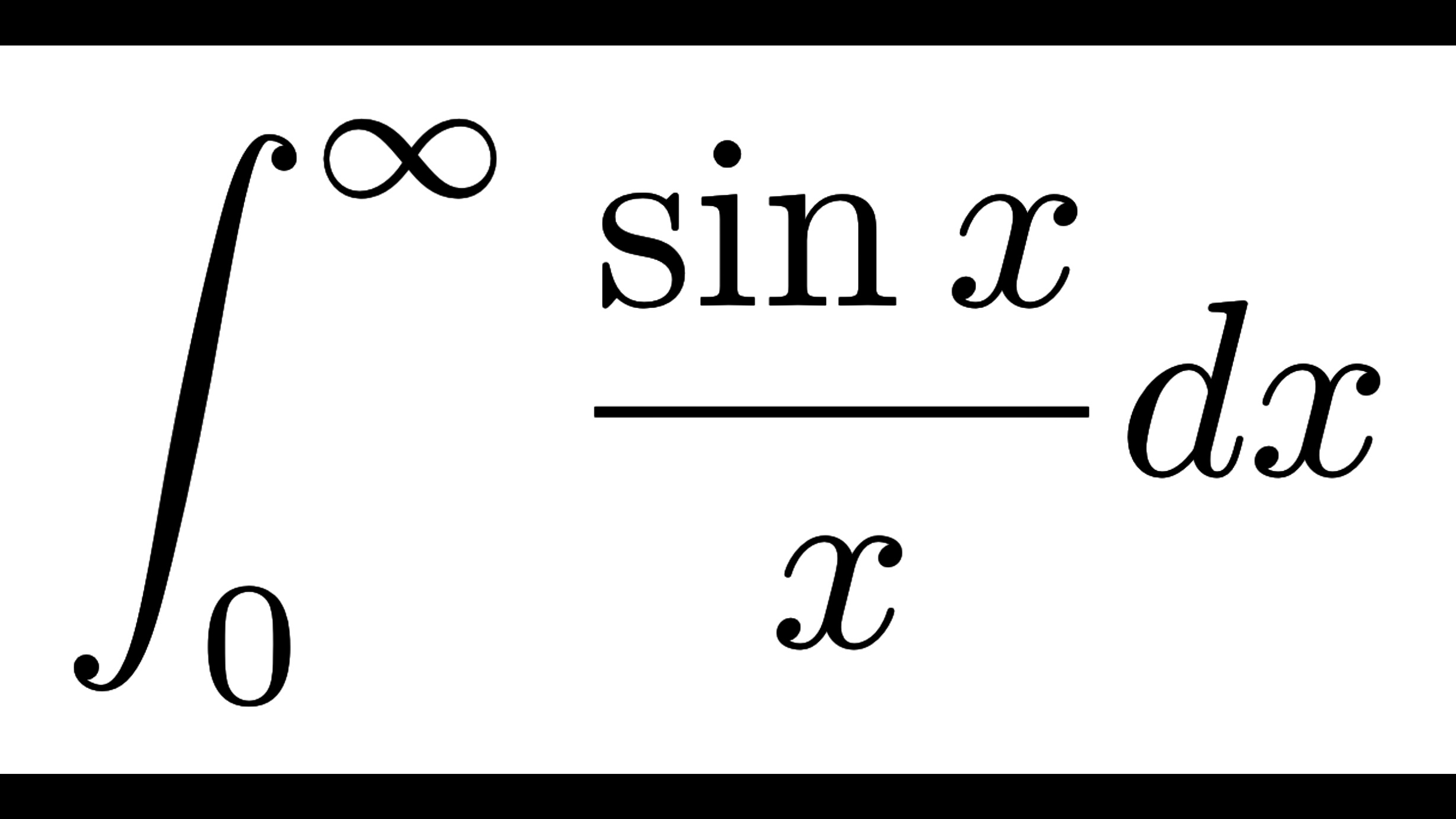
コメント