一般に、関数方程式 $$f(x+y)=f(x)+f(y)$$ を満たす関数 \(f\) は加法的であるといい、この関数方程式をコーシーの関数方程式 (Cauchy’s functional equation) と呼びます。
以前、定義域が実数全体である関数 \(f\) が加法的であることと
ある実数の定数 \(a\) を用いて $$f(x)=ax$$ と書ける。
ことが同値になるための十分条件をひとつ与える記事を書きました。
この記事では「関数 \(f\) がある一点で連続であること」が十分条件であることを確認しました。
今回はもう少し強く「解となる関数 \(f\) が連続であること」を仮定して、コーシーの関数方程式に似た以下の方程式を解いてゆきたいと思います。
- \(f\,\colon \mathbb{R}\to\mathbb{R}^\times\), \(\ \ f(x+y)=f(x)f(y)\)
- \(f\,\colon \mathbb{R}^\times\to\mathbb{R}\), \(\ \ f(xy)=f(x)+f(y)\)
- \(f\,\colon \mathbb{R}^\times\to\mathbb{R}^\times\), \(f(xy)=f(x)f(y)\)
但し、実数全体の集合を \(\mathbb{R}\) と書きます。また、\(0\) を除く実数全体の集合を \(\mathbb{R}^\times\) と書きます。
方程式1を解く。

コーシーの関数方程式と比べると右辺が積になってるから、両辺の対数をとれば和に直せそうだけど…。

\(f(x)\) の値は \(0\) ではないけど、負の数かもしれないから、その辺りを解決できたらいいな!
まず、関数方程式 \(f(x+y)=f(x)f(y)\) において、\(x=y\) とすると \(f(2x)=(f(x))^2\) となる。ここで、常に \(f(x)\neq0\) である。よって、\(2x\) を \(x\) に置き換えることで、常に \(f(x)>0\) であることがわかる。
次に、関数方程式 \(f(x+y)=f(x)f(y)\) の両辺の対数をとると $$\log f(x+y)=\log f(x)+\log f(y)$$ が成り立つ。よって、関数 \(g(x)=\log f(x)\) を考えると $$g(x+y)=g(x)+g(y)$$ を満たす。また、関数 \(f\) の連続性より、関数 \(g\) も連続である。これより、ある実数の定数 \(a\) を用いて $$g(x)=ax$$ と書ける。
さて、\(g(x)=\log f(x)\) であったので \(f(x)=e^{ax}\) となるが、正の定数 \(e^a\) を改めて \(a\) とおくことで $$f(x)=a^x$$ と書くことができる。

\(0\) にならないのが鍵なのか…。\(x=y\) とすることで \(f(x)\) が正の数に限定されるから結構自由に扱える感じがしたな。
方程式2を解く。

今度は左辺の変数の部分が積になってるけど、変数の対数をとるってどうすればいいんだろう。

変数の対数か。符号がわからないけど、例えば正の場合、その言葉通りに \(\log x=u\) としてみると \(x=e^u\) って変形できる…。何か使えそうなアイデアな気はするけど。
まず、関数方程式 \(f(xy)=f(x)+f(y)\) において、\(x=y\) とすると \(f(x^2)=2f(x)\) となる。ここで、$$f(-x)=\frac{1}{2}f((-x)^2)=\frac{1}{2}f(x^2)=f(x)$$ であるので、\(f\) は奇関数である。
次に、正の数 \(x,y\) に対して \(s=\log x\) 及び \(t=\log y\) を考えると \(x=e^s\) かつ \(y=e^t\) である。これを関数方程式 $$f(x+y)=f(x)f(y)$$ に代入すると $$f(e^{s+t})=f(e^s)+f(e^t)$$ が成り立つ。よって、関数 \(g(u)=f(e^u)\) を考えると $$g(s+t)=g(s)+g(t)$$ を満たす。また、関数 \(f\) の連続性より、関数 \(g\) も連続である。これより、ある実数の定数 \(a\) を用いて $$g(u)=au$$ と書ける。
さて、\(g(u)=f(e^u)\) であったので、改めて \(x=e^u>0\) とおくと \(f(x)=a\log x\) となる。
また、関数 \(f\) は奇関数であったので、\(x<0\) の場合も考慮することで $$f(x)=a\log|x|$$ と書くことができる。

この \(2\) 乗を作って奇関数であることを示すアイデアは勉強になるな。さっきと同じで、正の数に限定されると扱いやすい。
方程式3を解く。

そうくるだろうと思ってた。左辺の変数の部分と、右辺がそれぞれ積になってる。きっと、今までの二つの合わせ技でいけるのではないかな?

そうね。解の関数の形を知るために、正の実数のみに定義域を限定して部分的な解を求めても良さそう。もし奇関数なら上手く絶対値を作用させれば良い気もするし…。
まず、関数方程式 \(f(xy)=f(x)f(y)\) において、\(y=x\) とすると \(f(x^2)=(f(x))^2\) となる。ここで、常に \(f(x)\neq0\) である。よって、\(x^2\) を \(x\) に置き換えることで、\(x>0\) で常に \(f(x)>0\) であることがわかる。
また、\(y=-x\) とすると \(f(-x^2)=f(x)f(-x)\) となる。ここで、\(x<0\) とすると \(f(-x^2)>0\) かつ \(f(-x)>0\) であるので、\(x<0\) でも常に \(f(x)>0\) であることがわかる。
次に、関数 \(g(u)=\log f(e^u)\) を考えると、任意の実数 \(s,t\) について
\begin{align}
g(s+t)
&=\log f(e^{s+t})\\
&=\log f(e^se^t)\\
&=\log (f(e^s)f(e^t))\\
&=\log f(e^s)+\log f(e^t)\\
&=g(s)+g(t)
\end{align}を満たす。また、関数 \(f\) の連続性より、関数 \(g\) も連続である。これより、ある実数の定数 \(a\) を用いて $$g(u)=au$$ と書ける。
さて、\(g(u)=\log f(e^u)\) であったので \(f(e^u)=e^{au}\) となる。改めて \(x=e^u>0\) とおくと \(f(x)=x^a\) となる。
また、\(x<0\) のとき
\begin{align}
(f(x))^2
&=f(x^2)\\
&=f((-x)^2)\\
&=(f(-x))^2\\
&=((-x)^a)^2
\end{align}であって、\(f(x)>0\) であるので \(f(x)=(-x)^a\) となる。
以上より、$$f(x)=|x|^a$$ と書くことができる。

すぐに奇関数と言い切れなかったな。平方が等しいことと、符号の一致か…。いい経験には、なった。
最後に。

今回は、コーシーの関数方程式に帰着することによって解くことのできる関数方程式について考えてきました。
例えば、正の実数全体 \(\mathbb{R}^+\) 上の関数方程式 \(f(xy)=f(x)f(y)\) は、\(f\) が群の準同型であることを表しています。特に、それが連続でもあるなら、実数の定数 \(a\) を用いて $$f(x)=x^a$$ と書けることを確認しました。ここで、実数 \(X,Y\) を \(x=e^X\) かつ \(f(x)=e^Y\) によって定義すると $$Y=aX$$ という比例の関係が成り立ちます。
このように、乗法に関する連続な群の準同型があった場合、指数関数によって引き戻し、線型代数学の話題に持ち込むことができることが予想されます。この話題が気になった方は、リー群やリー代数について調べてみてください。
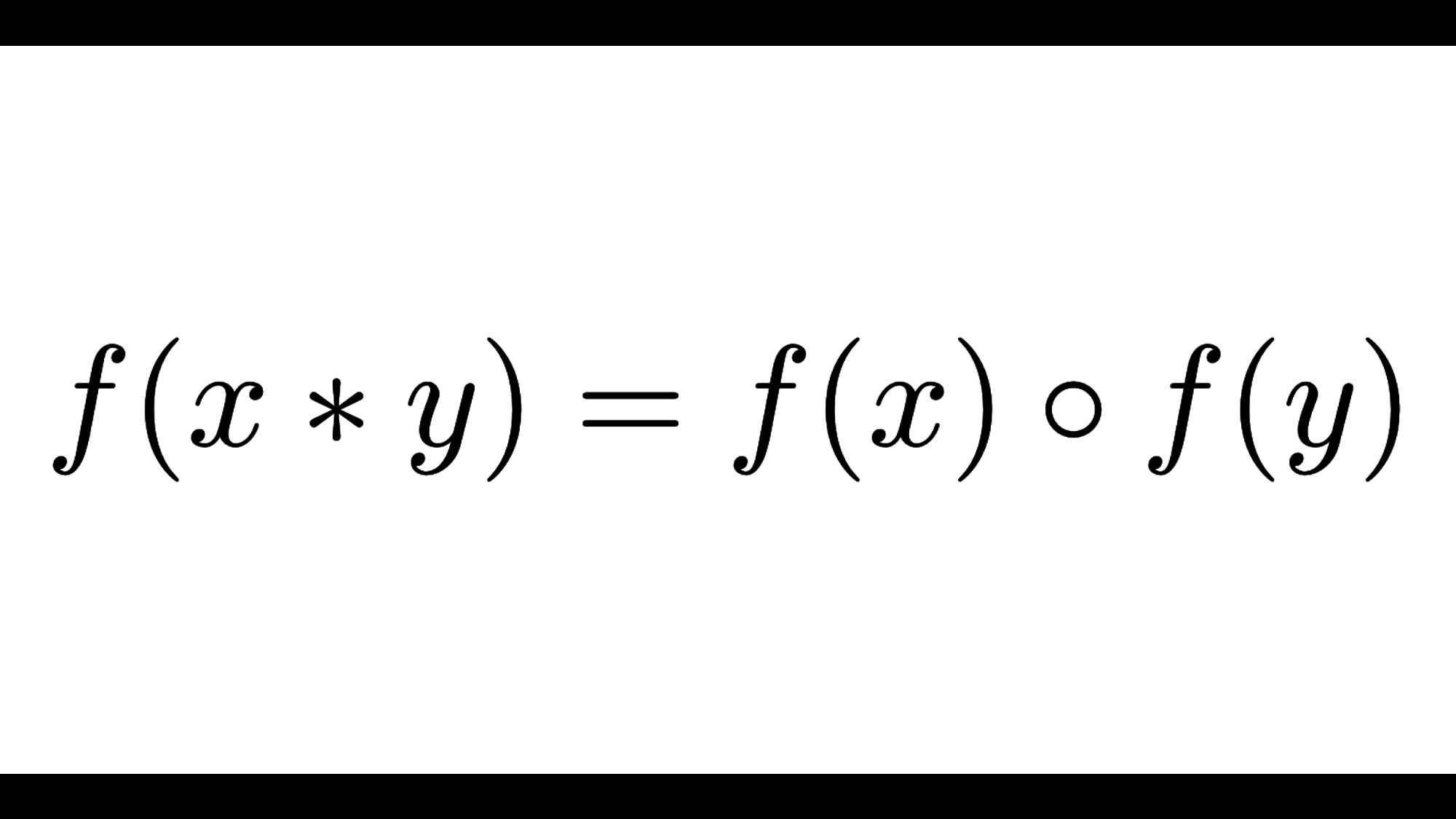
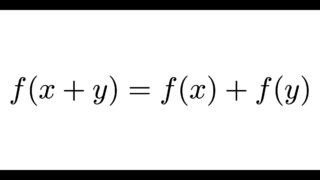
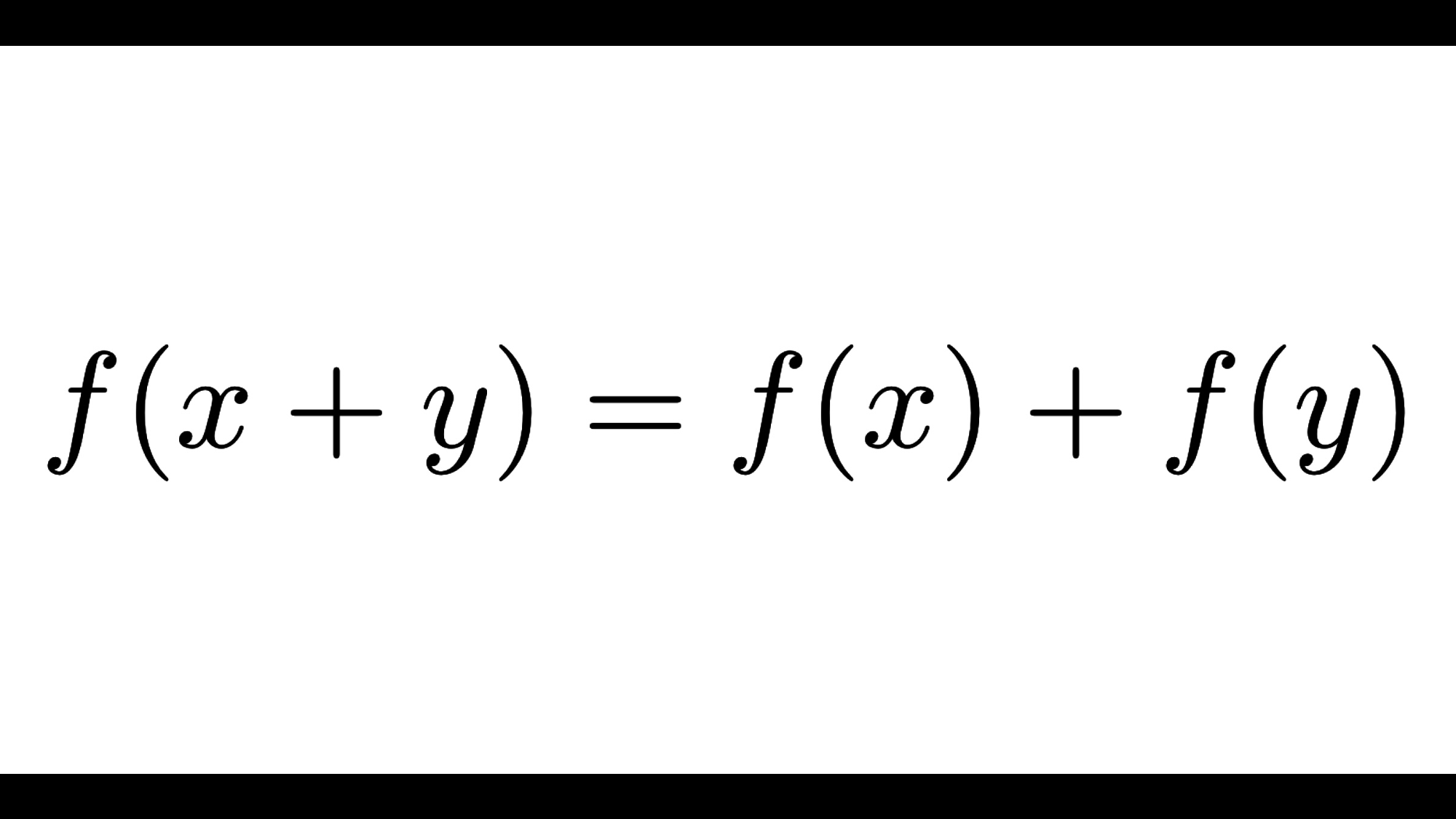

コメント