【東京工業大学】第４問「場合分けの目的」と「計算の手間」解答・解説［過去問 2023年度］

\(A\) と \(B\) の共通部分は \(xy\) 平面、\(yz\) 平面、\(zx\) 平面に関して対称であるので
\begin{align}
x&\geq0,&y&\geq0,&z&\geq0
\end{align}の部分の体積を考え、その対称性から \(8\) 倍すれば良い。

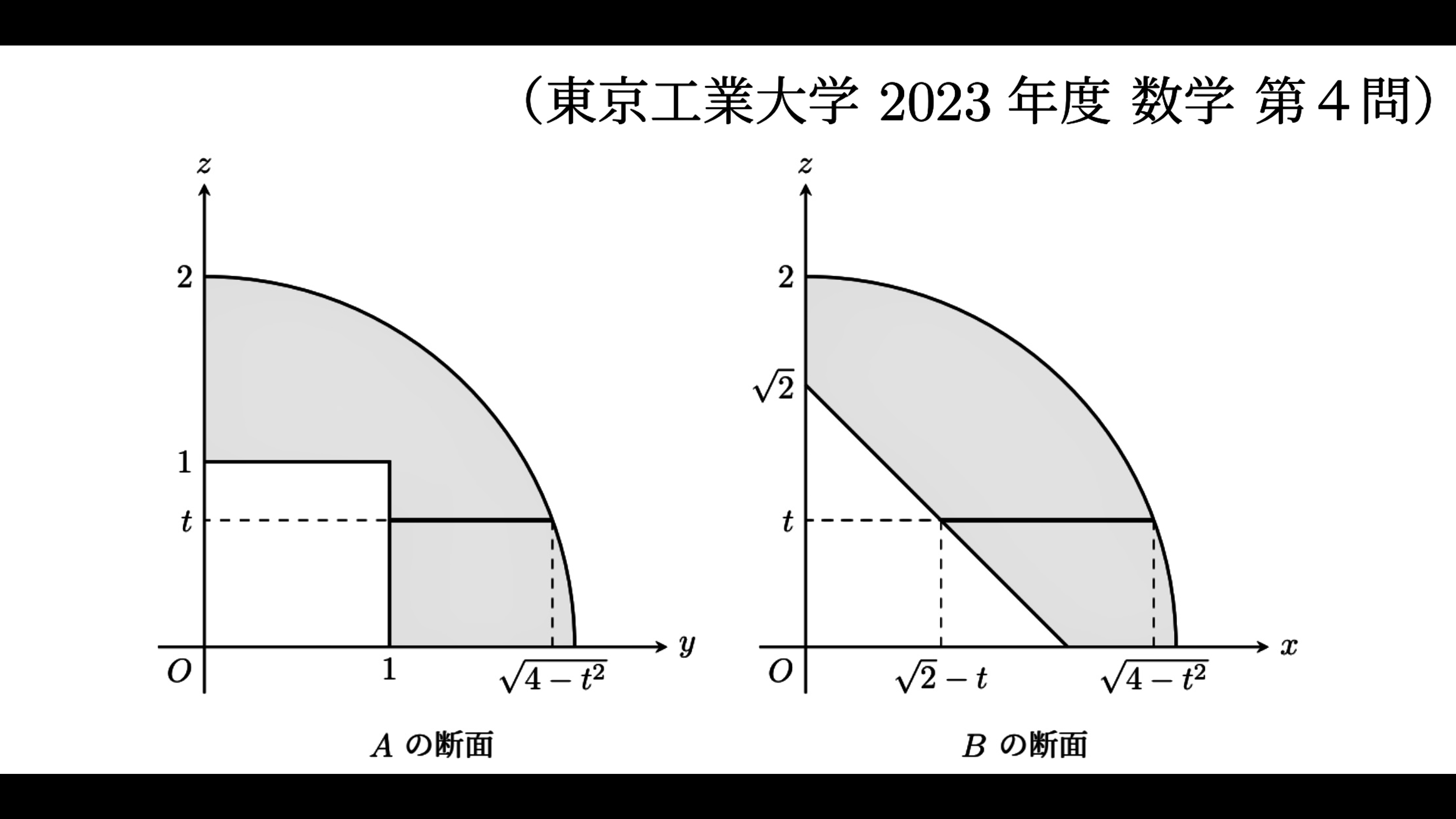
平面 \(z=t\) で \(A\) と \(B\) の共通部分を切って断面を考えるのために、まず、\(A\) と \(B\) をそれぞれ軸に垂直な平面で輪切りにした断面を見ておく。

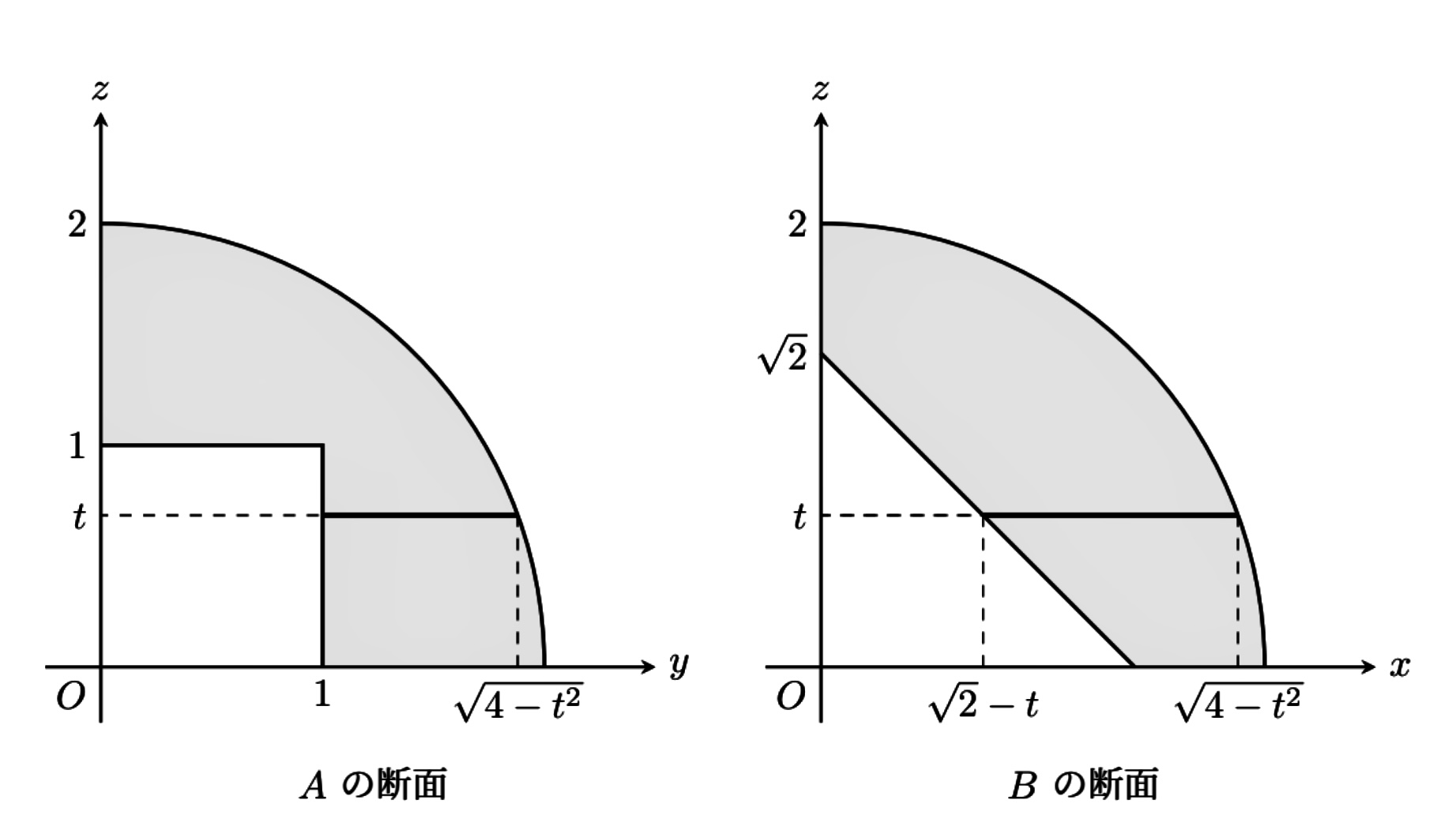
これより、\(z\) 座標に関して、\(3\) つの区間
\begin{align}
0\leq t\leq1,\ 1\leq t\leq\sqrt{2},\ \sqrt{2}\leq t\leq2
\end{align}に場合を分けて、平面 \(z=t\) による断面を見てゆく。

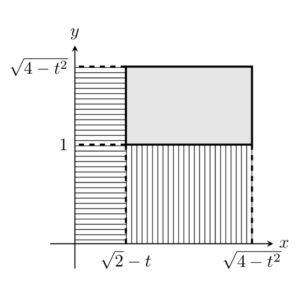
まず、\(0\leq t\leq1\) のとき。下図において、
\begin{align}
\begin{cases}
0\leq x\leq \sqrt{4-t^2}\\[3pt]
0\leq y\leq \sqrt{4-t^2}
\end{cases}
\end{align}の正方形 \(S_t\) から、\(B\) の取り除かれた角柱の部分（横線部）を引き、さらに、残る部分から \(A\) の取り除かれた角柱の部分（縦線部）を引けば良い。

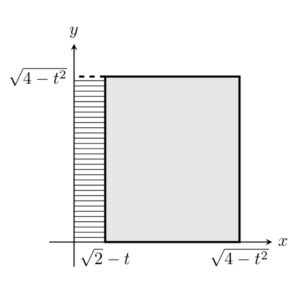
次に、\(1\leq t\leq\sqrt{2}\) のとき。下図において、正方形 \(S_t\) から、\(B\) の取り除かれた角柱の部分（横線部）を引けば良い。

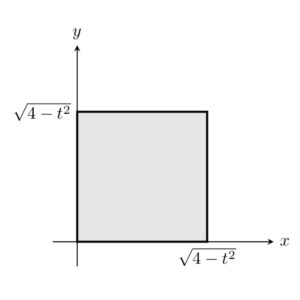
最後に、\(\sqrt{2}\leq t\leq2\) のとき。下図において、正方形 \(S_t\) のみ考えれば良い。

さて、

• 正方形 \(S_t\) の作る立体の体積 \(V_1\) は
  \begin{align}
  V_1&=\int_0^2 (4-t^2) dt
  \end{align}
• 横線の長方形の作る立体の体積 \(V_2\) は
  \begin{align}
  V_2&=\int_0^\sqrt{2} (\sqrt{2}-t)\sqrt{4-t^2} dt
  \end{align}
• 縦線の長方形の作る立体の体積 \(V_3\) は
  \begin{align}
  V_3&=\int_0^1 \left\{\sqrt{4-t^2}-(\sqrt{2}-t)\right\} dt
  \end{align}

ここで、\(t=2\sin\theta\) とおくと\begin{align}
\int \sqrt{4-t^2} dt
&=4\int \cos^2\theta d\theta\\
&=2\int (1+\cos 2\theta) d\theta\\
&=2\theta+\sin 2\theta+C
\end{align}となる。但し、\(C\) は積分定数である。

よって、求める体積を \(V\) とおくと

\begin{align}
\frac{V}{8}
&=V_1-V_2-V_3\\
&=\left(4\times2+\frac{2^3}{3}\right)\\
&\qquad-\left(\sqrt{2}\Bigl[2\theta+\sin 2\theta\Bigr]_0^{\frac{\pi}{4}}+\frac{1}{3}\left[(4-t^2)^{\frac{3}{2}}\right]_0^\sqrt{2}\right)\\
&\qquad-\left\{\Bigl[2\theta+\sin 2\theta\Bigr]_0^{\frac{\pi}{6}}-\left(\sqrt{2}-\frac{1}{2}\right)\right\}\\
&=\left(8+\frac{8}{3}\right)\\
&\qquad-\left(\frac{\sqrt{2}}{2}\pi+\sqrt{2}+\frac{2\sqrt{2}}{3}+\frac{8}{3}\right)\\
&\qquad-\left(\frac{\pi}{3}+\frac{\sqrt{3}}{2}-\sqrt{2}+\frac{1}{2}\right)\\
&=\frac{15}{2}-\frac{2\sqrt{2}}{3}-\frac{\sqrt{3}}{2}-\frac{\pi}{3}-\frac{\sqrt{2}}{2}\pi
\end{align}

すなわち

\begin{align}
V=60-\frac{16\sqrt{2}}{3}-4\sqrt{3}-\frac{8}{3}\pi-4\sqrt{2}\pi
\end{align}

となる。