みなさん、こんにちは。
今回は「今週の実積分」より、次の問題を解いてゆきたいと思います。
次の広義積分の値を求めよ。
$$I=\int_{-\infty}^\infty\frac{\cos x}{x^2+1}dx$$
複素積分に関する「コーシーの積分定理」や「留数定理」の実積分への応用の例題は 以下の記事 にまとめてゆく予定です。
複素関数論の講義の復習、期末試験やレポート、院試対策等に是非お役立て下さい!
【解答例】
関数 \(f(z)\) と経路 \(\Gamma\) の設定
まず、$$f(z)=\frac{e^{iz}}{z^2+1}$$ とし、積分経路として半径 \(R\) の上半円 \(\Gamma\) を考える。
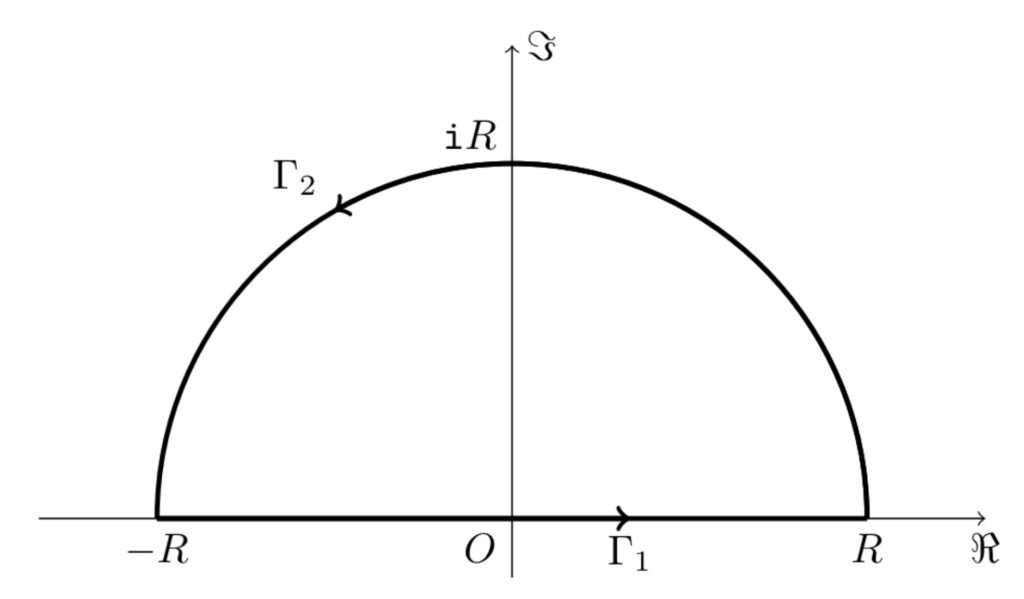
まず、各経路 \(\Gamma_1\),\(\Gamma_2\) 上での積分値を個別に考えてゆきます!
各 \(\Gamma_k\) 上で積分値を計算
\(\Gamma_1\) 上の積分値について
\(\Gamma_1\) 上において、\(z=x\) と置換すると $$dz=dx$$ であるので
\begin{align}
\int_{\Gamma_1}f(z)dz
&=\int_{-R}^Rf(x)dx\\
&=\int_{-R}^R\frac{\cos x+i\sin x}{x^2+1}dx\\
&=\int_{-R}^R\frac{\cos x}{x^2+1}dx+i\int_{-R}^R\frac{\sin x}{x^2+1}dx\\
&=\int_{-R}^R\frac{\cos x}{x^2+1}dx
\end{align}
より
\begin{align}
\int_{\Gamma_1}f(z)dz\to I\quad(R\to\infty)\tag{1}
\end{align}となる。
\(\Gamma_2\) 上の積分値について
\(\Gamma_2\) 上において、\(z=Re^{i\theta}\) とおくと $$dz=iRe^{i\theta}d\theta$$ であるので
\begin{align}
\int_{\Gamma_2}f(z)dz
&=\int_0^\pi f(Re^{i\theta})iRe^{i\theta}d\theta\\
&=iR\int_0^\pi \frac{e^{Rie^{i\theta}}e^{i\theta}}{R^2e^{2i\theta}+1}d\theta\\
&=iR\int_0^\pi \frac{e^{-R\sin\theta}e^{iR\cos\theta}e^{i\theta}}{R^2e^{2i\theta}+1}d\theta
\end{align}
である。
よって、\(R\) を十分大きくとると
\begin{align}
\left|\int_{\Gamma_2}f(z)dz\right|
&\leq R\int_0^\pi \frac{|e^{-R\sin\theta}e^{iR\cos\theta}e^{i\theta}|}{|R^2e^{2i\theta}+1|}d\theta\\
&\leq R\int_0^\pi \frac{e^{-R\sin\theta}}{R^2-1}d\theta\\
&=\frac{2R}{R^2-1}\int_0^{\frac{\pi}{2}}e^{-R\sin\theta}d\theta
\end{align}
が成り立つ。
ここで、\(\displaystyle 0\leq\theta\leq\frac{\pi}{2}\) において $$\frac{2}{\pi}\theta\leq\sin\theta$$ である(ジョルダンの不等式)ので
\begin{align}
\left|\int_{\Gamma_2}f(z)dz\right|
&\leq\frac{2R}{R^2-1}\int_0^{\frac{\pi}{2}}e^{-\frac{2R}{\pi}\theta}d\theta\\
&=\frac{2R}{R^2-1}\left[-\frac{\pi}{2R}e^{-\frac{2R}{\pi}\theta}\right]_0^{\frac{\pi}{2}}\\
&=\pi\frac{1-e^{-R}}{R^2-1}\\
&\to0\qquad(R\to\infty)
\end{align}すなわち
\begin{align}
\int_{\Gamma_2}f(z)dz\to0\quad(R\to\infty)\tag{2}
\end{align}となる。
一方、経路 \(\Gamma\) 全体で考えると、留数定理を適用することができます!
\(\Gamma\) 上で「留数定理」を適用
さて、十分大きな \(R\) について、関数 \(f(z)\) は閉曲線 \(\Gamma\) の囲む領域の内部に孤立特異点 \(z=i\) を持ち、それ以外で正則である。これは \(1\) 位の極なので、留数定理(Residue theorem)より
\begin{align}
\oint_\Gamma f(z)dz
&=2\pi i\ \underset{z=i}{\rm Res}f(z)\\
&=2\pi i\lim_{z\to i}\frac{e^{iz}}{z+i}\\
&=2\pi i\frac{1}{2ei}\\
&=\frac{\pi}{e}
\end{align}すなわち
\begin{align}
\int_{\Gamma_1}f(z)dz+\int_{\Gamma_2}f(z)dz=\frac{\pi}{e}\tag{3}
\end{align}が成り立つ。
さあ、準備は整いましたね!
極限をとり積分値 \(I\) を得る
式 (3) において極限 \(R\to\infty\) を考えると、式 (1)、(2) より
\begin{align}
I+0=\frac{\pi}{e}
\end{align}すなわち
\begin{align}
I=\frac{\pi}{e}
\end{align}を得る。
これで求めたい積分値を得ることができました。
お疲れ様でした!!
解説動画の紹介

本記事は、YouTube「今週の実積分」で公開されている以下の動画を基に作成されています。
不明な箇所があった場合やお気づきの点等ございましたらコメントをお願いします。
ありがとうございました!
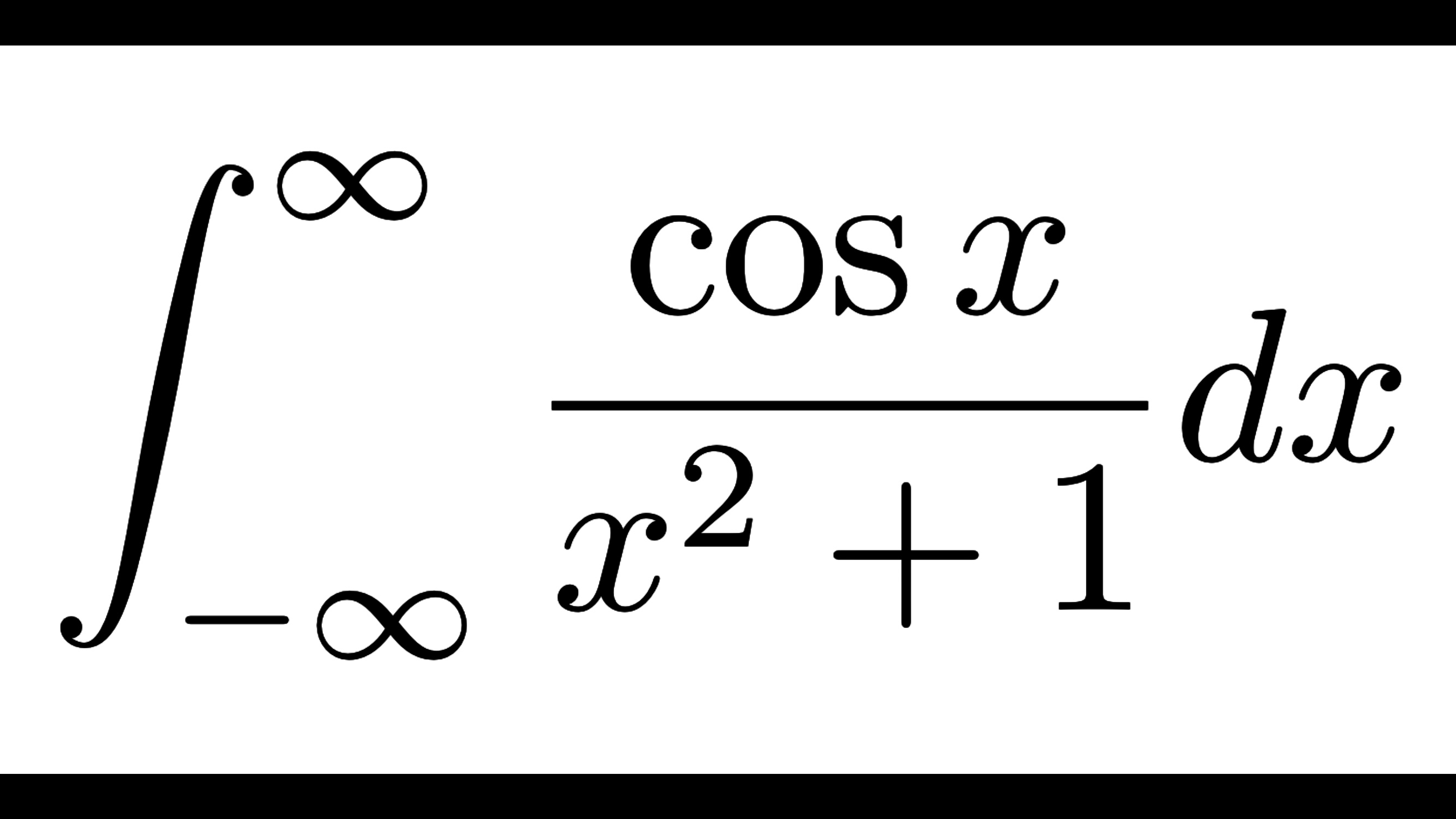
コメント