みなさん、こんにちは。
今回は「今週の実積分」より、次の問題を解いてゆきたいと思います。
次の定積分の値を求めよ。
$$I=\int_0^{2\pi}\frac{1}{5+3\cos\theta}d\theta$$
複素積分に関する「コーシーの積分定理」や「留数定理」の実積分への応用の例題は 以下の記事 にまとめてゆく予定です。
複素関数論の講義の復習、期末試験やレポート、院試対策等に是非お役立て下さい!
【解答例】
経路 \(\Gamma\) の設定
まず、積分経路として単位円周 \(\Gamma\colon |z|=1\) を考える。
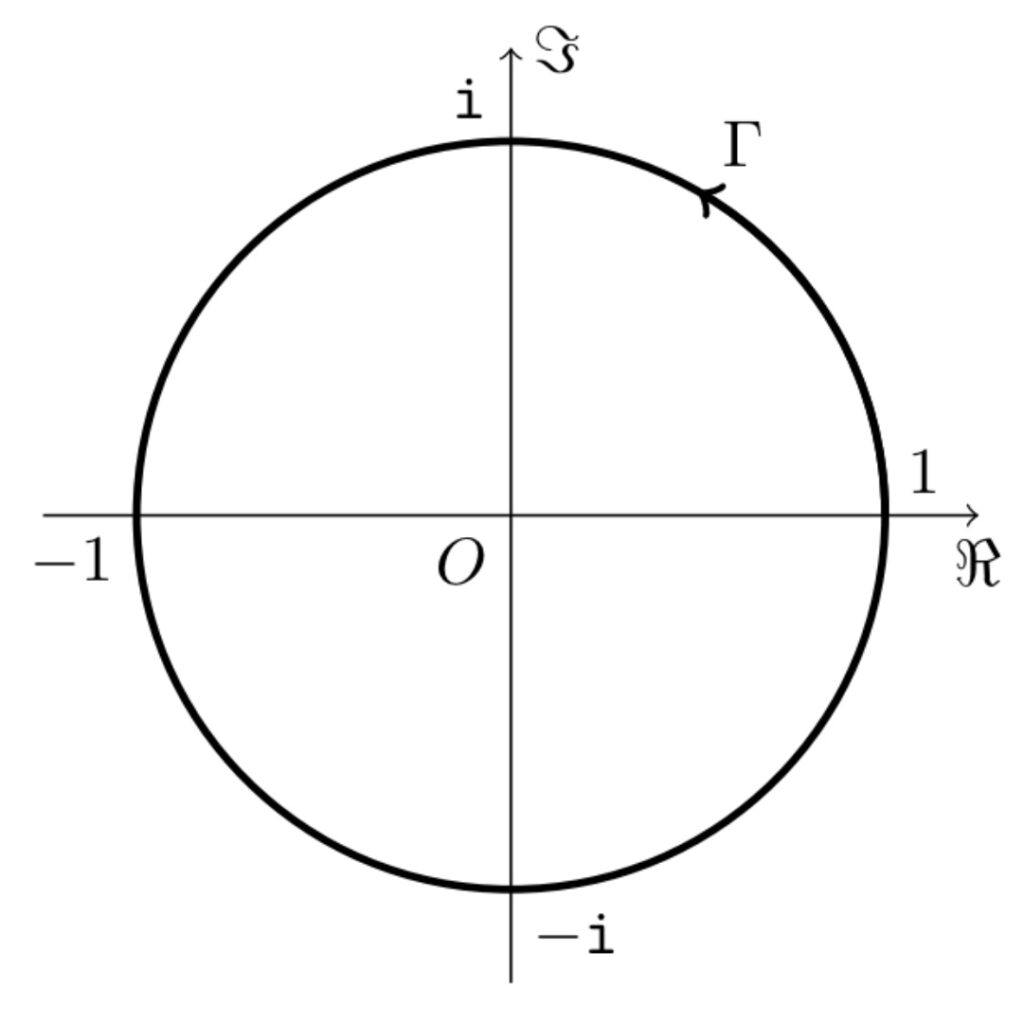
積分値 \(I\) を \(\Gamma\) 上の積分で表示
\(\Gamma\) 上において、\(z=e^{i\theta}\) と置換すると $$dz=ie^{i\theta}d\theta$$ すなわち $$\frac{1}{iz}dz=d\theta$$ であるので
\begin{align}
I
&=\int_0^{2\pi}\frac{1}{5+3\cos\theta}d\theta\\
&=\oint_{|z|=1}\frac{1}{5+3\dfrac{z+z^{-1}}{2}}\frac{1}{iz}dz\\
&=\frac{2}{i}\oint_{|z|=1}\frac{1}{10z+3(z^2+1)}dz\\
&=\frac{2}{i}\oint_{|z|=1}\frac{1}{3z^2+10z+3}dz\\
&=\frac{2}{i}\oint_{|z|=1}\frac{1}{(3z+1)(z+3)}dz\tag{1}
\end{align}
となる。
この形まで持ち込むと、あの定理を適用することができます!
\(\Gamma\) 上で「留数定理」を適用
さて、$$f(z)=\dfrac{1}{(3z+1)(z+3)}$$ とおくと、関数 \(f(z)\) は閉曲線 \(|z|=1\) の囲む領域の内部に孤立特異点 \(\displaystyle z=-\frac{1}{3}\) を持ち、それ以外で正則なので、留数定理(Residue theorem)より
\begin{align}
&\oint_{|z|=1}\frac{1}{(3z+1)(z+3)}dz\\
&\quad=2\pi i\ \underset{z=-\frac{1}{3}}{\rm Res}f(z)\\
&\quad=2\pi i\lim_{z\to-\frac{1}{3}}\frac{1}{3(z+3)}\\
&\quad=2\pi i\times\frac{1}{8}\\
&\quad=\frac{\pi i}{4}\tag{2}
\end{align}となる。
さあ、求める値はもう目の前です!
以上より積分値 \(I\) を得る
以上、式 (1)、(2) より
\begin{align}
I
&=\frac{2}{i}\oint_{|z|=1}\frac{1}{(3z+1)(z+3)}dz\\
&=\frac{2}{i}\times\frac{\pi i}{4}\\
&=\frac{\pi}{2}
\end{align}を得る。
これで、求めたい積分値を得ることができました。
お疲れ様でした!!
解説動画の紹介

本記事は、YouTube「今週の実積分」で公開されている以下の動画を基に作成されています。
本記事や本サイトに関する感想等、お気軽にお寄せ下さい。
参考になれば幸いです!
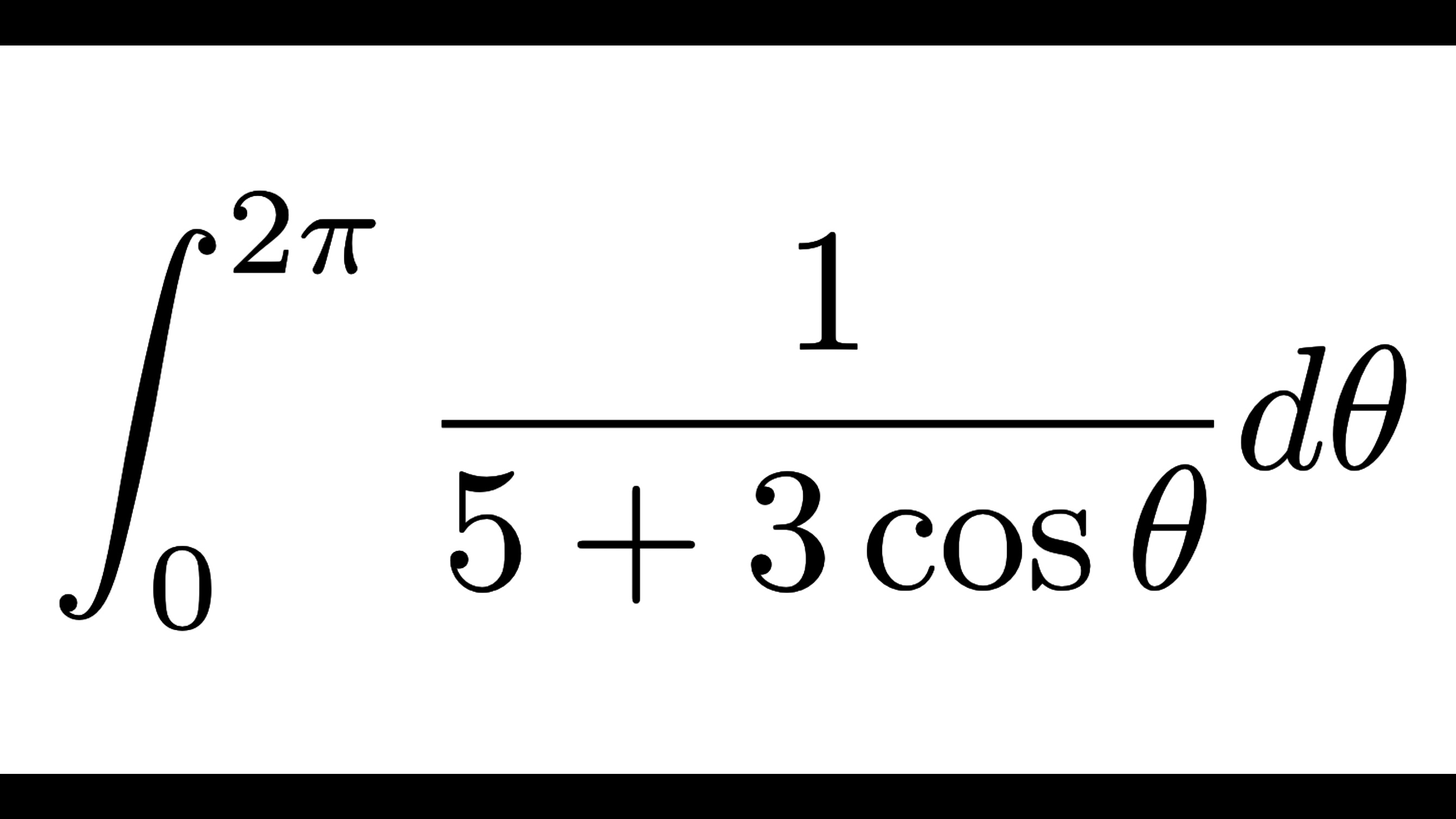
コメント