みなさん、こんにちは。
今回は「今週の実積分」より、次の問題を解いてゆきたいと思います。
次の広義積分の値を求めよ。
\begin{align}
I&=\int_0^\infty\cos x^2 dx,\\
J&=\int_0^\infty\sin x^2 dx
\end{align}
※この広義積分は フレネル積分(Fresnel integral)と呼ばれます。
複素積分に関する「コーシーの積分定理」や「留数定理」の実積分への応用の例題は 以下の記事 にまとめています。
複素関数論の講義の復習、期末試験やレポート、院試対策等に是非お役立て下さい!
【解答例】
関数 \(f(z)\) と経路 \(\Gamma\) の設定
まず、$$f(z)=e^{iz^2}$$ とし、積分経路として半径 \(R\) で中心角 \(\displaystyle \frac{\pi}{4}\) の扇形の閉曲線 \(\Gamma\) を考える。
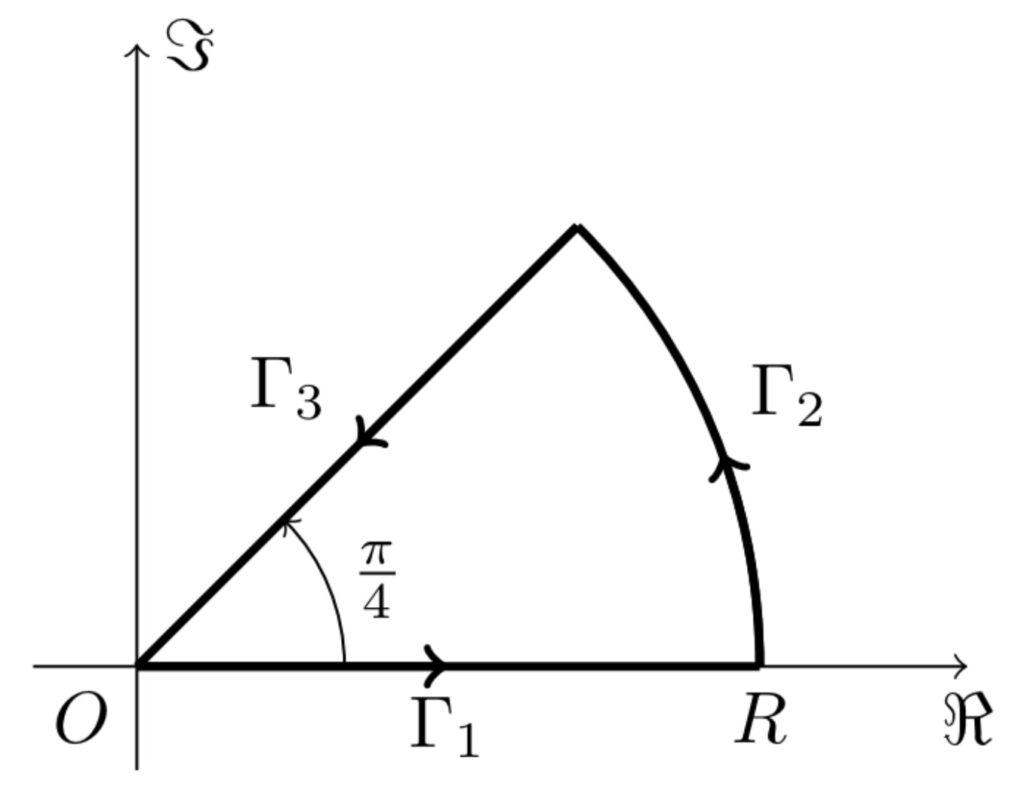

まず、各経路 \(\Gamma_1\),\(\Gamma_2\),\(\Gamma_3\) 上での積分値を個別に考えてゆきます!
各 \(\Gamma_k\) 上で積分値を計算
\(\Gamma_1\) 上の積分値について
\(\Gamma_1\) 上において、\(z=x\) と置換すると \(dz=dx\) であるので
\begin{align}
&\int_{\Gamma_1}f(z)dz\\
&\quad=\int_0^Re^{ix^2}dx\\
&\quad=\int_0^R(\cos x^2+i\sin x^2)dx\\
&\quad=\int_0^R\cos x^2dx+i\int_0^R\sin x^2dx\\
&\quad\to I+iJ\qquad(R\to\infty)\tag{1}
\end{align}
となる。
\(\Gamma_2\) 上の積分値について
\(\Gamma_2\) 上において、\(z=Re^{i\theta}\) と置換すると \(dz=iRe^{i\theta}d\theta\) であるので
\begin{align}
\int_{\Gamma_2}f(z)dz
&=\int_0^{\frac{\pi}{4}} e^{iR^2e^{2i\theta}}iRe^{i\theta}d\theta\\
&=iR\int_0^{\frac{\pi}{4}} e^{iR^2\cos2\theta}e^{-R^2\sin2\theta}e^{i\theta}d\theta
\end{align}
となる。
よって、
\begin{align}
\left|\int_{\Gamma_2}f(z)dz\right|
&\leq R\int_0^{\frac{\pi}{4}} \left|e^{iR^2\cos2\theta}e^{-R^2\sin2\theta}e^{i\theta}\right|d\theta\\
&=R\int_0^{\frac{\pi}{4}}e^{-R^2\sin2\theta}d\theta
\end{align}
である。
ここで、\(\displaystyle 0\leq\theta\leq\frac{\pi}{4}\) において $$\frac{4}{\pi}\theta\leq\sin2\theta$$ である(ジョルダンの不等式)ので
\begin{align}
\left|\int_{\Gamma_2}f(z)dz\right|
&\leq R\int_0^{\frac{\pi}{4}} e^{-\frac{4R^2}{\pi}\theta}d\theta\\
&=R\left[-\frac{\pi}{4R^2}e^{-\frac{4R^2}{\pi}\theta}\right]_0^{\frac{\pi}{4}}\\
&=\pi\frac{1-e^{-R^2}}{4R}\\
&\to0\qquad(R\to\infty)
\end{align}すなわち
\begin{align}
\int_{\Gamma_2}f(z)dz\to0\quad(R\to\infty)\tag{2}
\end{align}となる。
\(\Gamma_3\) 上の積分値について
\(\Gamma_3\) 上において、\(z=xe^{\frac{\pi}{4}i}\) と置換すると \(dz=e^{\frac{\pi}{4}i}dx\) であるので
\begin{align}
\int_{\Gamma_3}f(z)dz
&=\int_R^0 e^{-x^2}e^{\frac{\pi}{4}i}dx\\
&=-e^{\frac{\pi}{4}i}\int_0^R e^{-x^2}dx
\end{align}となる。ここで、Gauss積分より $$\int_0^\infty e^{-x^2}dx=\frac{\sqrt{\pi}}{2}$$ であるので
\begin{align}
\int_{\Gamma_3}f(z)dz\to-\frac{\sqrt{\pi}}{2}e^{\frac{\pi}{4}i}\quad(R\to\infty)\tag{3}
\end{align}
となる。
一方、経路 \(\Gamma\) 全体で考えると、あの定理を適用することができます!
\(\Gamma\) 上で「積分定理」を適用
さて、関数 \(f(z)\) は閉曲線 \(\Gamma\) の囲む領域の境界と内部で正則なので、コーシーの積分定理(Cauchy’s integral theorem)より
\begin{align}
\oint_\Gamma f(z)dz=0
\end{align}すなわち
\begin{align}
\int_{\Gamma_1}f(z)dz+\int_{\Gamma_2}f(z)dz+\int_{\Gamma_3}f(z)dz=0\tag{4}
\end{align}
が成り立つ。
さあ、準備は整いましたね!
極限をとり積分値 \(I\) を得る
式 (4) において極限 \(\varepsilon\to+0\),\(R\to\infty\) を考えると、式 (1)、(2)、(3) より
\begin{align}
(I+iJ)+0+\left(-\frac{\sqrt{\pi}}{2}e^{\frac{\pi}{4}i}\right)=0
\end{align}すなわち
\begin{align}
I=J=\frac{1}{2}\sqrt{\frac{\pi}{2}}
\end{align}を得る。
これで求めたい積分値を得ることができました。
お疲れ様でした!!
解説動画の紹介


本記事は、YouTube「今週の実積分」で公開されている以下の動画を基に作成されています。
不明な箇所があった場合はコメントをお願いします。
みなさんの参考になれば幸いです!
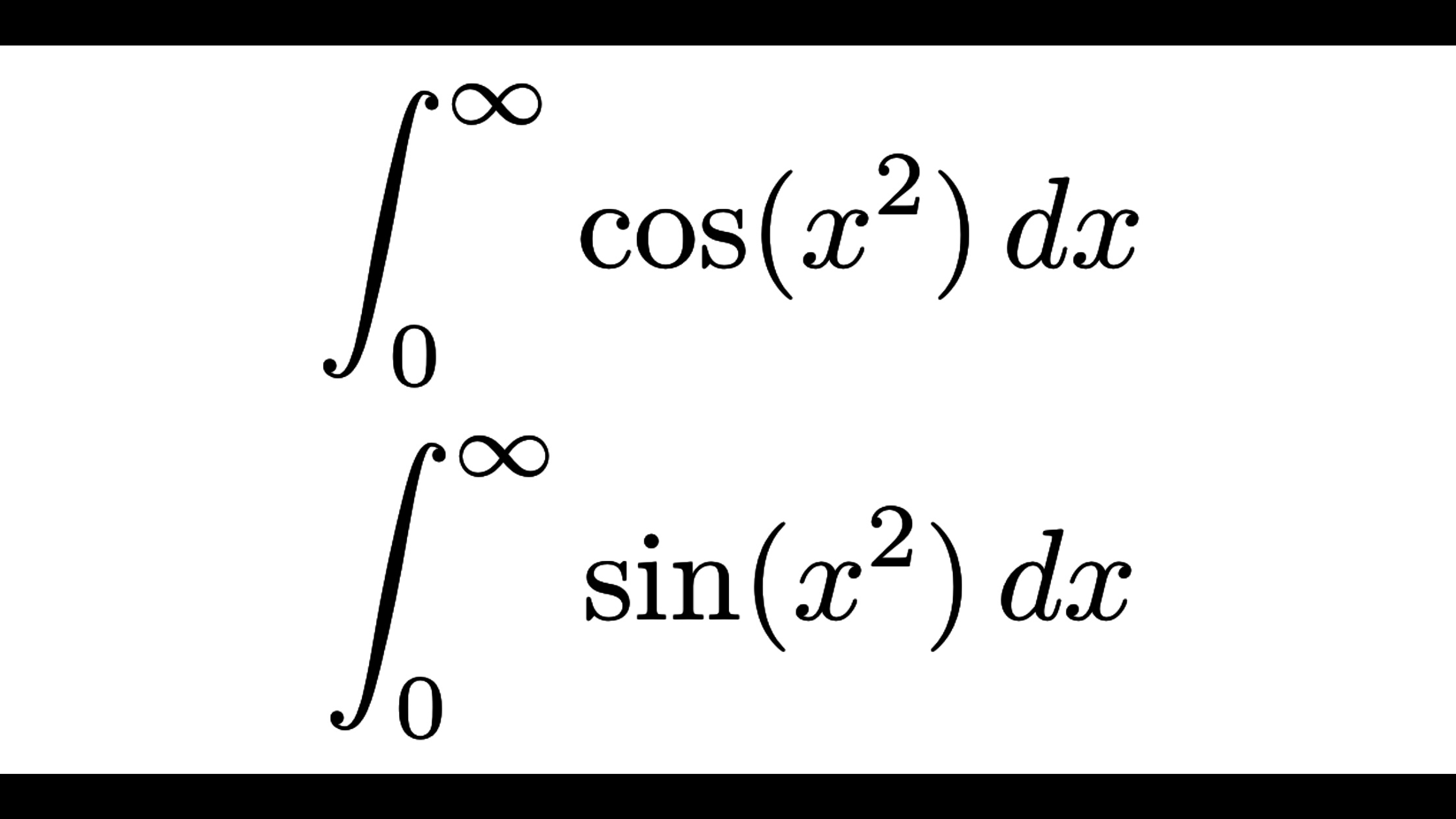
コメント