 数学IIIC
数学IIIC 【∫[0,π/2] sin^n(x) dx】定積分の漸化式 Part.1 三角関数(1)ウォリス積分
今回は [0,π/2] 上の定積分 I_n=∫sin^n(x)dx や J_n=∫cos^n(x)dx に関する問題を解きます。これは「ウォリス積分」とも呼ばれます。二重階乗を用いることで、一般項を簡潔に記述することもできます。
 数学IIIC
数学IIIC  数学IIIC
数学IIIC 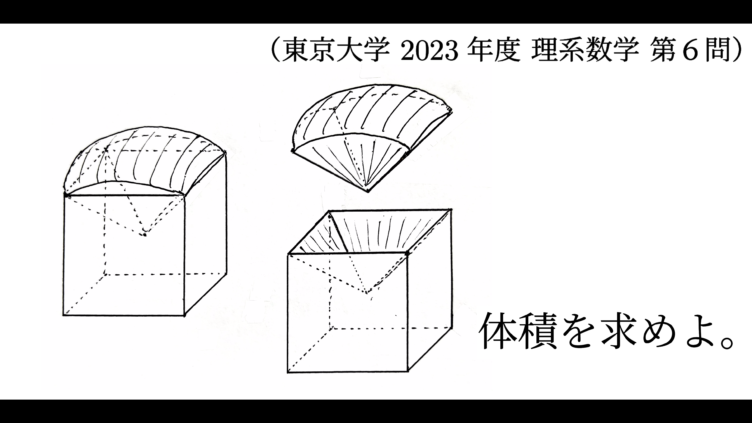 大学入試
大学入試  大学入試
大学入試 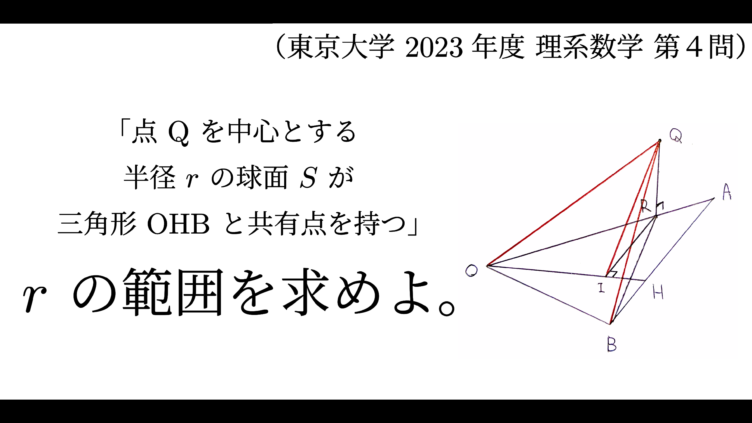 大学入試
大学入試  大学入試
大学入試  大学入試
大学入試  大学入試
大学入試 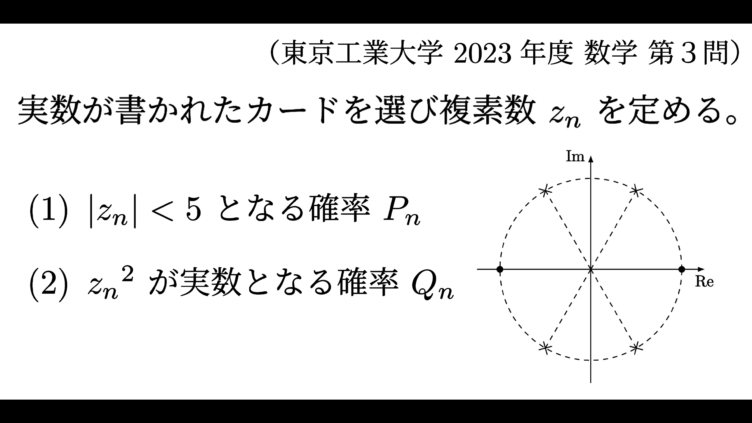 大学入試
大学入試 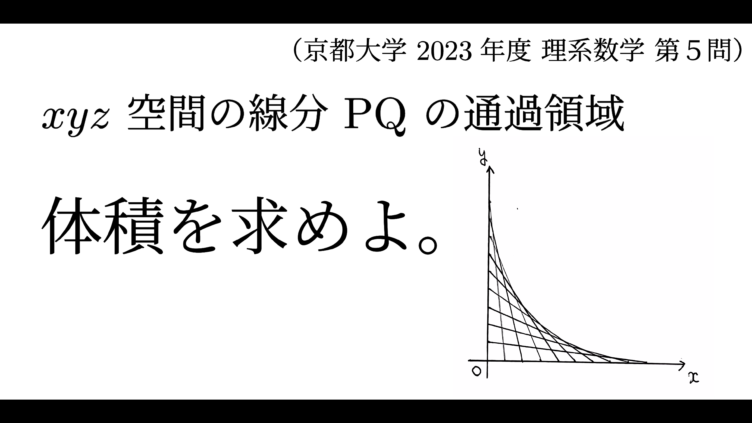 大学入試
大学入試