一般に、関数方程式
\begin{align}
f(x+y)=f(x)+f(y)\tag{1}
\end{align}を満たす関数 \(f\) は加法的であるといい、関数方程式 \((1)\) をコーシーの関数方程式 (Cauchy’s functional equation) と呼びます。例えば、 $$f(x)=ax$$ なる関数 \(f\) は加法的です。
本記事では、大学受験数学でも扱われるテーマである「関数方程式」の中でも基本的かつ有名なコーシーの関数方程式を満たす実数変数の関数 \(f\) について考えます。
高校数学で考える!

\(f\) が実数全体で微分可能であるとき

関数 \(f\) が微分可能なので、とりあえず微分してみるとわかることがあります。
まず、コーシーの関数方程式 \((1)\) において \(x=y=0\) とすると \(f(0)=2f(0)\) であるので
\begin{align}
f(0)=0
\end{align}であることがわかる。一方、コーシーの関数方程式 \((1)\) の両辺を \(y\) に関して微分すると
\begin{align}
f^\prime(x+y)=f^\prime(y)
\end{align}となるので、\(y=0\) とすることによって \(f^\prime(x)=f^\prime(0)\) が成り立つ。ここで、定数 \(f^\prime(0)\) を \(a\) とおくと
\begin{align}
f^\prime(x)=a
\end{align}となる。よって、\(f(0)=0\) であることから
\begin{align}
f(x)=ax
\end{align}を得る。
\(f\) が点 \(0\) で微分可能であるとき

コーシーの関数方程式の両辺を無闇に微分することはできませんが、関数 \(f\) が点 \(0\) において微分可能であれば実数全体で微分可能であることが証明できます。
まず、コーシーの関数方程式より \(f(0)=0\) であることがわかる。一方、点 \(x\) における微分係数を考えると、関数方程式 \((1)\) より
\begin{align}
\lim_{h\to0}\frac{f(x+h)-f(x)}{h}
&=\lim_{h\to0}\frac{f(h)}{h}\\
&=\lim_{h\to0}\frac{f(h)-f(0)}{h}\\
&=f^\prime(0)
\end{align}
となる。これより、任意の実数 \(x\) において \(f\) は微分可能であって
\begin{align}
f^\prime(x)=a
\end{align}となる。ここで、定数 \(f^\prime(0)\) を \(a\) とおいた。よって、\(f(0)=0\) であることから
\begin{align}
f(x)=ax
\end{align}を得る。
\(f\) がある点 \(x_0\) で微分可能であるとき

関数 \(f\) が実数全体で微分可能であることを証明するために点 \(0\) における微分係数を考えましたが、一般に、微分可能である点 \(x_0\) が存在すれば同様の議論ができることがわかります。
まず、\(f(0)=0\) である。一方、点 \(x\) における微分係数を考えると、関数方程式 \((1)\) より
\begin{align}
\lim_{h\to0}\frac{f(x+h)-f(x)}{h}
&=\lim_{h\to0}\frac{f(h)}{h}\\
&=\lim_{h\to0}\frac{f(x_0+h)-f(x_0)}{h}\\
&=f^\prime(x_0)
\end{align}
となる。これより、関数 \(f\) は微分可能であって
\begin{align}
f^\prime(x)=a
\end{align}となる。ここで、定数 \(f^\prime(x_0)\) を \(a\) とおいた。よって、\(f(0)=0\) であることから
\begin{align}
f(x)=ax
\end{align}を得る。
条件なしでもわかることは?

\(x\) が自然数なら \(f(x)=ax\)

これまでの議論は、何らかの微分可能性を仮定することによって得られていました。一方、\(f(0)=0\) はコーシーの関数方程式のみから得られていたわけです。このように条件を仮定することなくわかることを探ってみましょう。
\(n\) を自然数とする。
コーシーの関数方程式 \((1)\) において \(x=n\), \(y=1\) とすると
\begin{align}
f(n+1)=f(n)+f(1)
\end{align}が成り立つ。
よって、数列 \(\{f(n)\}\) は初項と公差が共に \(f(1)\) である等差数列である。
これより \(f(n)=f(1)n\) であるので、\(a=f(1)\) とおくことで
\begin{align}
f(n)=an
\end{align}を得る。
\(x\) が整数でも \(f(x)=ax\)

\(x>0\) なら自然数ですので \(ax\) になることはわかっていて、\(x=0\) のときも \(0\) になることがわかっていますね。
残るは \(x<0\) の場合ですが、\(-x>0\) ですから、自然数の場合をうまく活用したいところです。
\(m\) を整数とする。
まず、\(m\geq0\) ならば \(f(m)=am\) である。ただし、\(a=f(1)\) とおいた。
次に、\(m<0\) ならば \(-m>0\) である。コーシーの関数方程式 \((1)\) において \(x=m\), \(y=-m\) とすると
\begin{align}
f(0)&=f(m)+f(-m)
\end{align}すなわち
\begin{align}
0&=f(m)+a(-m)
\end{align}となるので \(f(m)=am\) が成り立つ。
以上より、任意の整数 \(m\) に対して
\begin{align}
f(m)=am
\end{align}を得る。
\(x\) が有理数であっても \(f(x)=ax\)

ここでは、自然数に対する議論で初項と公差が共に \(f(1)\) である等差数列 \(\{f(n)\}\) を用いました。
同様に、関数方程式 \((1)\) において \(x=ny\) とすると \(f((n+1)y)=f(ny)+f(y)\) となるので、数列 \(\{f(ny)\}\) は初項と公差が共に \(f(y)\) である等差数列になることがわかりますね。つまり
\begin{align}
f(ny)=nf(y)
\end{align}となるので、これを利用してみましょう。
\(r\) を有理数とする。
このとき、自然数 \(n\) と整数 \(m\) を用いて \(\displaystyle r=\frac{m}{n}\) すなわち \(nr=m\) と書けるので、\(a=f(1)\) とおくことで
\begin{align}
f(nr)&=f(m)\\
nf(r)&=am\\
f(r)&=\frac{am}{n}
\end{align}すなわち
\begin{align}
f(r)&=ar
\end{align}を得る。
連続であれば \(f(x)=ax\) となる!


さて、\(x\) が有理数ならば \(f(x)=ax\) と書けることがわかりました。これが \(x\) が実数であっても成り立つことを保証するためには、どのような条件を考えれば良いでしょうか。
考える数を有理数から実数に拡張したとき、何をしたのか思い出す必要がありそうですね。
有理数とは、整数の比で与えられるような数で、数直線上に表現することができます。逆に、数直線上に表現可能な数が必ず整数の比で与えられるか考えると、\(\sqrt{2}\) は不可能であることが知られています。
このように、いくらでも密に存在しそうな有理数でも “到達できない数” を含めて数直線を考えます。例えば、\(\sqrt{2}\) は有理数からなる数列
\begin{align}
&1.4,\\
&1.41,\\
&1.414,\\
&1.4142,\\
&1.41421,\\
&1.414213,\\
&1.4142135,\\
&1.41421356,\\
&\vdots
\end{align}の極限になっています。ちなみに、この数列の一般項はガウス記号を用いて \([\sqrt{2}\times10^n]\times10^{-n}\) と書くことができます。
このように、有理数列の全ての極限を有理数に添加したものを実数と呼ぶのです。(これを「完備化」と言います。)つまり、
任意の実数 \(x\) は
ある有理数列 \(\{r_n\}\) を用いて
\(\displaystyle x=\lim_{n\to\infty}r_n\) と表現できる
ことが言えます。(有理数全体の集合は実数全体の集合の「稠密な部分集合」であると言います。)
\(x\) を実数とする。
今、関数 \(f\) がある一点 \(x_0\) で連続であると仮定する。このとき、関数方程式 \((1)\) より
\begin{align}
\lim_{h\to0}(f(x+h)-f(x))
&=\lim_{h\to0}f(h)\\
&=\lim_{h\to0}(f(x_0+h)-f(x_0))\\
&=0
\end{align}
となる。これより、関数 \(f\) は連続であるので、\(\displaystyle x=\lim_{n\to\infty}r_n\) より
\begin{align}
f(x)
&=\lim_{n\to\infty}f(r_n)\\
&=\lim_{n\to\infty}ar_n\\
&=ax
\end{align}を得る。
最後に。

今回は、実数変数の関数 \(f\) に対してある「一点での連続性」を仮定したとき、加法的である(コーシーの関数方程式を満たす)ためには、ある定数 \(a\) を用いて $$f(x)=ax$$ と書けることが必要十分であることを確認しました。
深くは立ち入りませんが、その仮定を外すと関数 \(f\) は “ハメル基底” と呼ばれるものをを用いて無数に構成できることが知られています。詳しくは こちら をご覧ください。
コーシーの関数方程式に帰着できる類似の関数方程式がいくつかあります。
以下の記事で紹介していますので、ご覧ください。
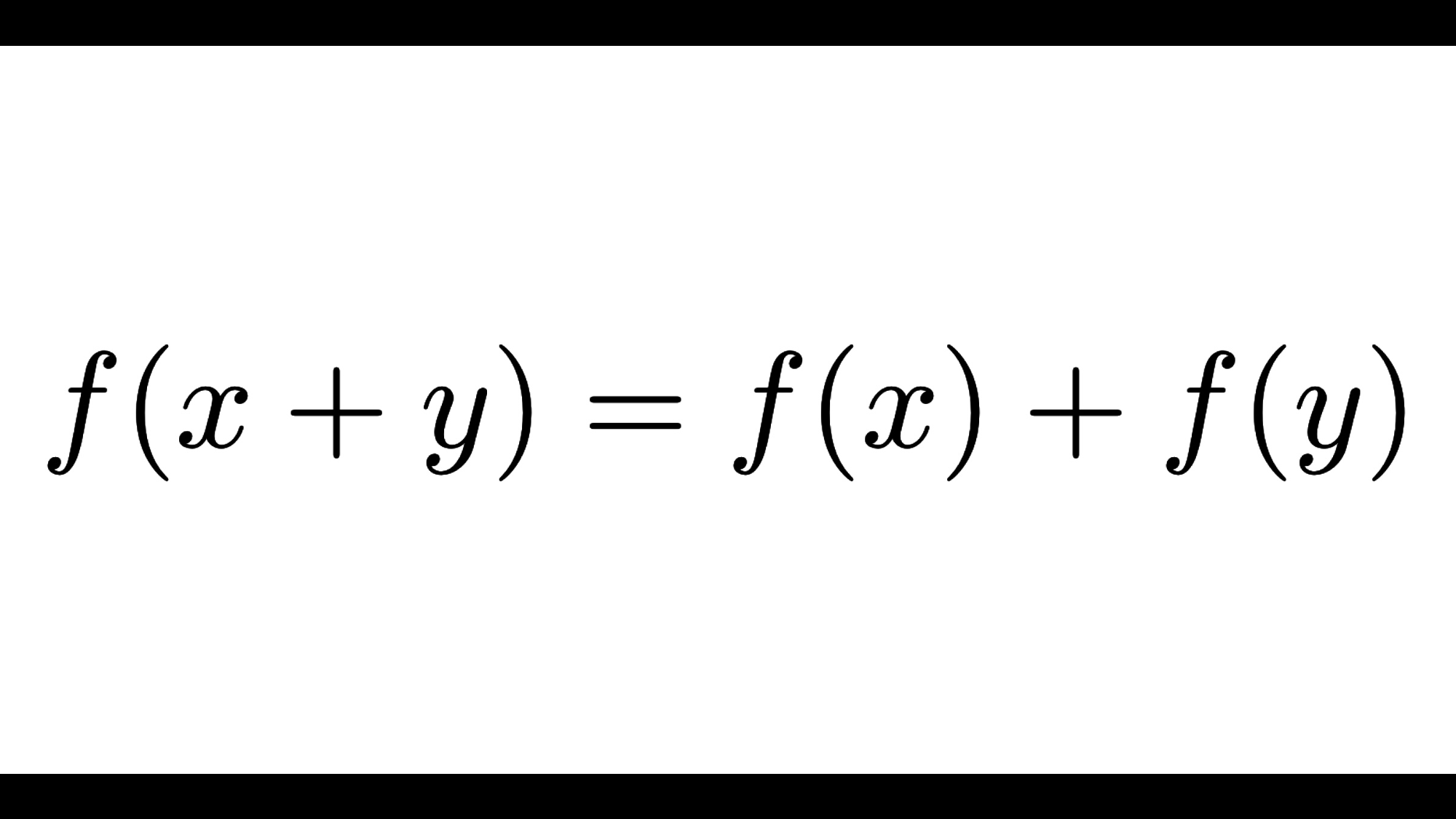
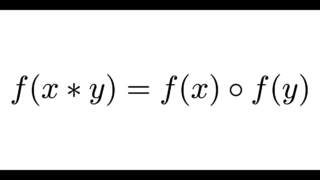
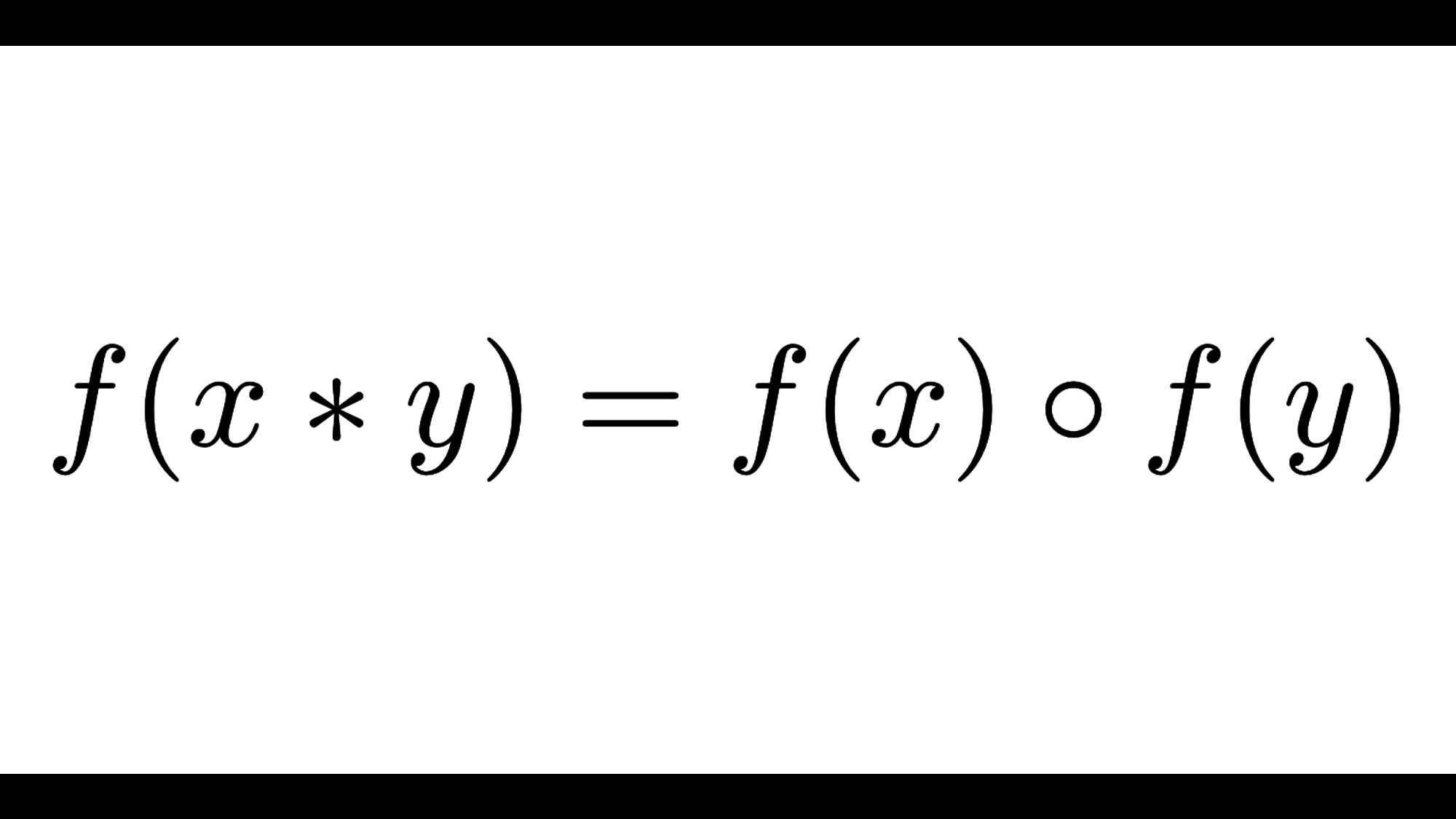
コメント