みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
正の整数 \(m\),\(n\) に対して、次の定積分
\begin{align}
B(m,n)&=\int_0^1 x^{m-1}(1-x)^{n-1} \,dx
\end{align}
を考える。但し、\(x^0\),\((1-x)^0\) は共に \(1\) とする。
(1)\(B(m,1)\) を求めよ。
(2)\(n\geq2\) とする。部分積分によって $$B(m,n)=\frac{n-1}{m}B(m+1,n-1)$$ を示せ。
(3)\(B(m,n)\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle B(m,1)=\frac{1}{m}\)
(2)省略。
(3)\(\displaystyle B(m,n)=\frac{(m-1)!(n-1)!}{(m+n-1)!}\)
解説

\(B(m,1)\) を求める。
まず、\((1-x)^0=1\) と約束していたので、
\begin{align}
B(m,1)
&=\int_0^1 x^{m-1}\,dx\\
&=\left[\frac{1}{m}x^m \right]_0^1\\
&=\frac{1}{m}
\end{align}となります。
\(B(m,n)\) の漸化式を求める。
\(n\geq2\) であることを用いて部分積分を行います。
\begin{align}
B(m,n)
&=\int_0^1 x^{m-1}(1-x)^{n-1} \,dx\\
&=\left[\frac{1}{m}x^m(1-x)^{n-1}\right]_0^1-\int_0^1 \frac{1}{m}x^m\left\{(n-1)(-1)(1-x)^{n-2}\right\}\,dx\\
&=0+\frac{n-1}{m}\int_0^1 x^m(1-x)^{n-2} \,dx\\
&=\frac{n-1}{m}B(m+1,n-1)
\end{align}
を得ます。
\(B(m,n)\) を求める。
\(n\geq2\) とすると、(2)より
\begin{align}
B(m,n)
&=\frac{n-1}{m}\times B(m+1,n-1)\\
&=\frac{n-1}{m}\times \frac{n-2}{m+1}\times B(m+2,n-2)\\
&\qquad\ \ \vdots\\
&=\frac{n-1}{m}\times \frac{n-2}{m+1}\times\cdots\times\frac{1}{m+n-2}\times B(m+n-1,1)
\end{align}
となります。(1)より $$B(m+n-1,1)=\frac{1}{m+n-1}$$ なので
\begin{align}
B(m,n)
&=\frac{n-1}{m}\times \frac{n-2}{m+1}\times\cdots\times\frac{1}{m+n-2}\times \frac{1}{m+n-1}\\
&=\frac{(m-1)!(n-1)!}{(m+n-1)!}
\end{align}
を得ます。
これは、(1)より \(n=1\) のときも成り立ちます。
よって、$$B(m,n)=\frac{(m-1)!(n-1)!}{(m+n-1)!}$$ となります。
最後に

今回は、ベータ関数 と呼ばれる関数
\begin{align}
B(x,y)=\int_0^1 t^{x-1}(1-t)^{y-1} \,dt
\end{align}
が題材になっています。この関数は「実部が正である複素数の組 \((x,y)\) 」に対して定義できるので、それを「正の整数」として \(B(m,n)\) を考えました。
さて、冒頭の \(B(m,n)\) の定積分において $$x=\sin^2\theta$$ と置換してみましょう。このとき、
\begin{align}
x^{m-1}&=\sin^{2m-2}\theta\\
(1-x)^{n-1}&=\cos^{2n-2}\theta
\end{align}
また
\begin{align}
dx&=2\sin\theta\cos\theta d\theta
\end{align}
であるので
\begin{align}
B(m,n)
&=\int_0^1 x^{m-1}(1-x)^{n-1} \,dx\\
&=\int_0^{\frac{\pi}{2}} \sin^{2m-2}\theta\,\cos^{2n-2}\theta\,(2\sin\theta\cos\theta)\,d\theta\\
&=2\int_0^{\frac{\pi}{2}} \sin^{2m-1}\theta\,\cos^{2n-1}\theta\,d\theta
\end{align}
を得ます。
ここで、
\begin{align}
I_{m,n}=\int_0^{\frac{\pi}{2}} \sin^m\theta\,\cos^n\theta\,d\theta
\end{align}
という定積分を考えると $$B(m,n)=2I_{2m-1,2n-1}$$ が成り立ちます。
この定積分 \(I_{m,n}\) については、以下の記事で扱っています。
関連 : 数学IIICカテゴリー

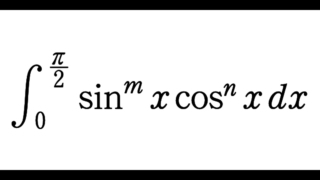

コメント