実数 $$\int_0^{2023} \frac{2}{x+e^x} dx$$ の整数部分を求めよ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】
被積分関数を \(\displaystyle f(x)=\frac{2}{x+e^x}\) とおき、整数部分を求める実数を
\begin{align}
I=\int_0^{2023} f(x) dx
\end{align}とおく。
まず、\(0\leq x\leq 2023\) において $$f(x)\leq\frac{2}{0+e^x}=2e^{-x}$$ であって、等号が成り立つのは \(x=0\) のときのみ。よって、
\begin{align}
I
&<\int_0^{2023} 2e^{-x} dx\\
&=\left[-2e^{-x}\right]_0^{2023}\\
&=2(1-e^{-2023})\\
&<2\tag{1}
\end{align}を得る。
次に、\(\displaystyle f(x)=\frac{2e^{-x}}{xe^{-x}+1}\) であるので、関数
\begin{align}
g(x)&=xe^{-x}&&(0\leq x\leq 2023)
\end{align}を上から評価する。今、
\begin{align}
g^\prime(x)=(1-x)e^{-x}
\end{align}であるので、\(g(x)\) は
- \(0\leq x\leq 1\) で単調に増加する。
- \(1\leq x\leq 2023\) で単調に減少する。
これより、\(g(x)\leq g(1)=e^{-1}\) すなわち $$f(x)\geq\frac{2e^{-x}}{e^{-1}+1}$$ であって、等号が成り立つのは \(x=1\) のときのみ。よって、
\begin{align}
I
&>\int_0^{2023} \frac{2e^{-x}}{e^{-1}+1} dx\\
&=\frac{2(1-e^{-2023})}{e^{-1}+1}
\end{align}である。ここで、\(e>2\) であるので
\begin{align}
I
&>\frac{2(1-2^{-2023})}{2^{-1}+1}\\
&=\frac{4}{3}\left(1-\frac{1}{2^{2023}}\right)\\
&>\frac{4}{3}\left(1-\frac{1}{2^2}\right)\\
&=\frac{4}{3}\times\frac{3}{4}\\
&=1\tag{2}
\end{align}を得る。
式 (1)、(2) より \(1<I<2\) であるので、求める整数部分は \(1\) である。
私が考えたこと

最終的に何を目指すか?
被積分関数 \(\displaystyle f(x)=\frac{2}{x+e^x}\) について、そのまま積分を具体的に計算することは難しい。そこで、定積分の値が評価できそうな関数で \(f(x)\) を評価し、
\begin{align}
n\leq \int_0^{2023}f(x)dx<n+1
\end{align}なる整数 \(n\) を見出したい。このとき、求める整数部分は \(n\) である。
上からの評価について。
関数 \(f(x)\) は \(0 \leq x \leq 2023\) で単調に減少する。特に分母について、\(x\geq0\) を用いることで
- \(\displaystyle f(x)\leq\frac{2}{0+e^x}=2e^{-x}\) と上から評価できる。
- \(\displaystyle f(x)\leq\frac{2}{x+e^0}=\frac{2}{x+1}\) と上から評価できる。
一次関数 \(x\) に比べて指数関数 \(e^x\) の方が非常に速く増加するため、これらでは前者の方が評価の精度が高い。しかも、実際に定積分を計算した値 $$\int_0^{2023}2e^{-x}dx=2\left(1-e^{-2023}\right)$$ の評価も難しくない。
下からの評価について。
その1
一方、下からも同様に \(x\leq2023\) を用いて $$f(x)\geq\frac{2}{2023+e^x}$$ と評価してみる。この右辺を
\begin{align}
\frac{2}{2023+e^x}=\frac{2e^{-x}}{2023e^{-x}+1}\tag{A}
\end{align}と変形すると積分の計算が可能となるが、そのまま
\begin{align}
\int_0^{2023} \frac{2e^{-x}}{2023e^{-x}+1} dx
&=\left[-\frac{2}{2023}\log\left(2023e^{-x}+1\right)\right]_0^{2023}\\
&=\frac{2}{2023}\log\frac{2024}{2023e^{-2023}+1}
\end{align}
と計算して具体的に評価するのは少し難しい。そこで、さらに被積分関数の評価を進め、\(x\geq 0\) より $$f(x)\geq\frac{2e^{-x}}{2023e^{-0}+1}=\frac{2e^{-x}}{2024}$$ としても $$\int_0^{2023}\frac{2e^{-x}}{2024}dx=\frac{1-e^{-2023}}{1012}$$ と計算できるが、評価としては精度が低い。
その2
上記の評価が甘かった反省としては
「一次関数 \(x\) と指数関数 \(e^{-x}\) の評価を独立に行なったこと」
がある。そこで、式 (A) の変形を参考に
\begin{align}
f(x)=\frac{2e^{-x}}{xe^{-x}+1}
\end{align}としてみる。これを下から評価したいので、分母に現れる関数 \(xe^{-x}\) を上から評価する。少なくとも、\(x\) と \(e^{-x}\) を独立に考えて $$xe^{-x}\leq2023e^{-0}=2023$$ と評価した上記の場合よりは精度の高い評価が得られるはずである。
その3
それでも上手くいかなかった場合、関数 \(f(x)\) が下に凸であることから、適切な接点を設定し、接線を利用して評価する方法もある。
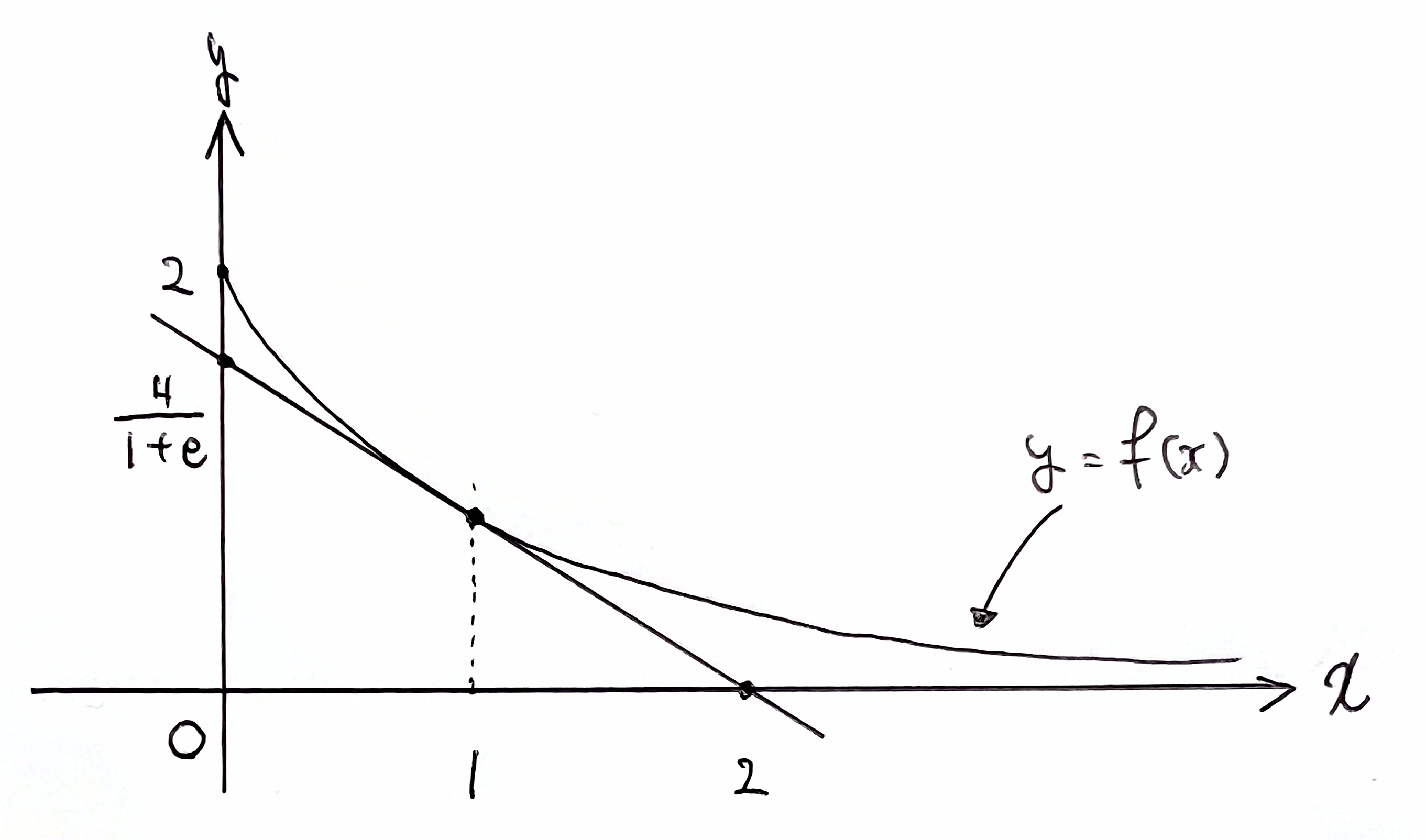
感想

積分区間は \([0,2023]\) と長いですが、ネイピア数について \(e>2\) であるので、少なくとも \(x=12\) あたりから被積分関数 \(f(x)\) の値は \(\displaystyle \frac{1}{2023}\) を下回ります。
関数 \(f(x)\) は指数関数 \(e^x\) によって非常に速く \(0\) に収束してゆきますが、仮に \(I\) の整数部分が \(0\) である場合、解答は実質 \(I<1\) の確認のみになってしまいます。
それも勿論あり得ますが、上下からの適切な評価を要請するために分子を \(2\) にしたのかもしれない(が、決めつけてはいけない)と思いつつ考察を進めました。
実際の値としては
- \(\displaystyle \int_0^{2023} \frac{2}{x+e^x} dx=1.61279123\cdots\) → 詳細
- \(\displaystyle \int_0^{2023} \frac{1}{x+e^x} dx=0.80639561\cdots\) → 詳細
になるそうです…!

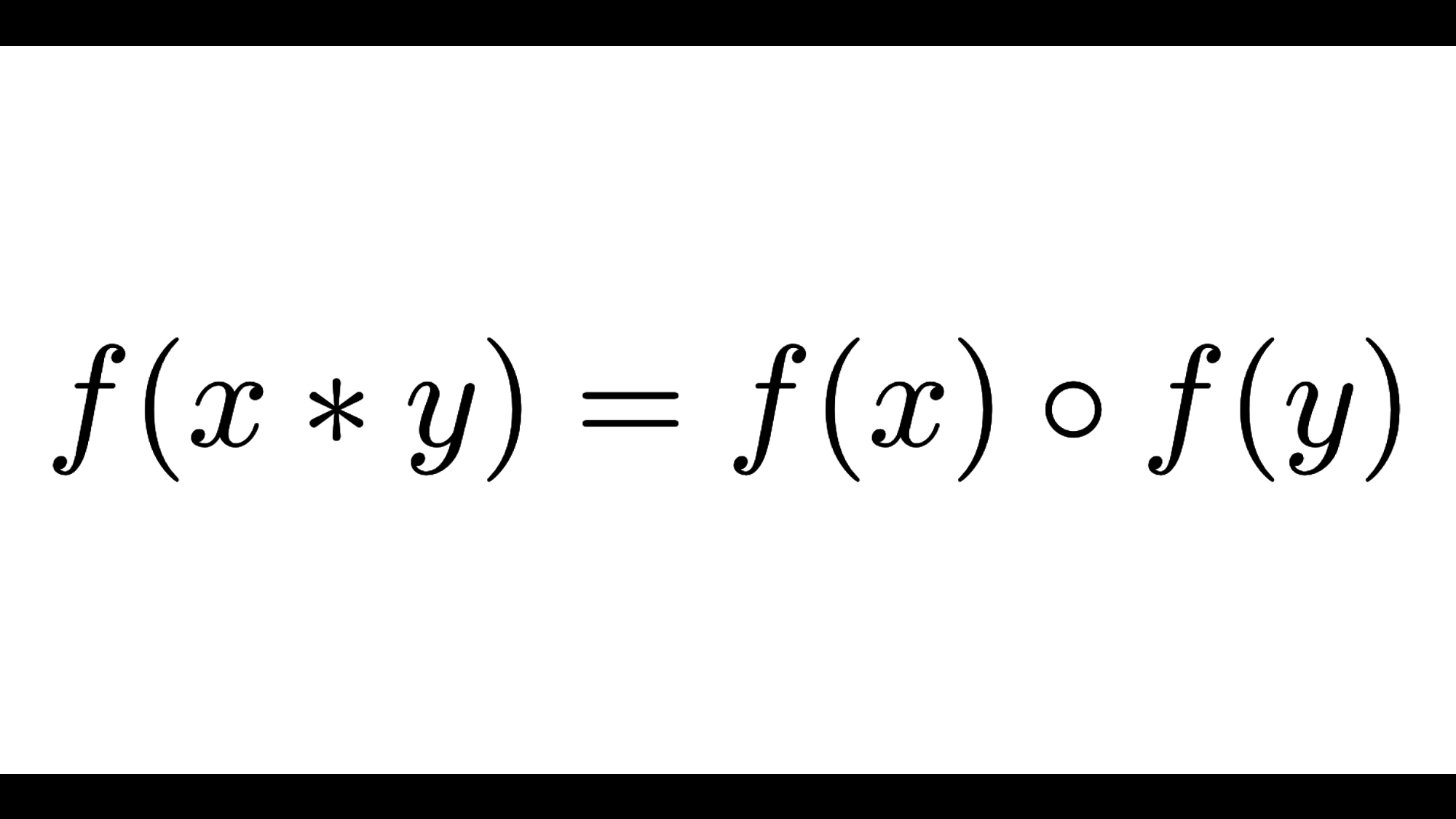

コメント