\(xyz\) 空間の \(4\) 点 \({\rm A}(1, 0, 0)\),\({\rm B}(1, 1, 1)\), \({\rm C}(-1, 1, -1)\),\({\rm D}(-1, 0, 0)\) を考える。
(1)\(2\) 直線 \({\rm AB}\),\({\rm BC}\) から等距離にある点全体のなす図形を求めよ。
(2)\(4\) 直線 \({\rm AB}\),\({\rm BC}\),\({\rm CD}\),\({\rm DA}\) に共に接する球面の中心と半径の組を全て求めよ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】

(1)
点 \({\rm P}\) から直線 \({\rm AB}\) に下ろした垂線の足を \({\rm H}\) とする。このとき、\(\triangle{\rm PBH}\) は $$\angle{\rm PHB}=90^\circ$$ の直角三角形である。直線 \({\rm AB}\) の方向ベクトルとして大きさが \(1\) の \(\displaystyle \frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}\) を考えると
\begin{align}
{\rm BH}
=\left|\overrightarrow{\rm BP}\cdot\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}\right|
\end{align}である。
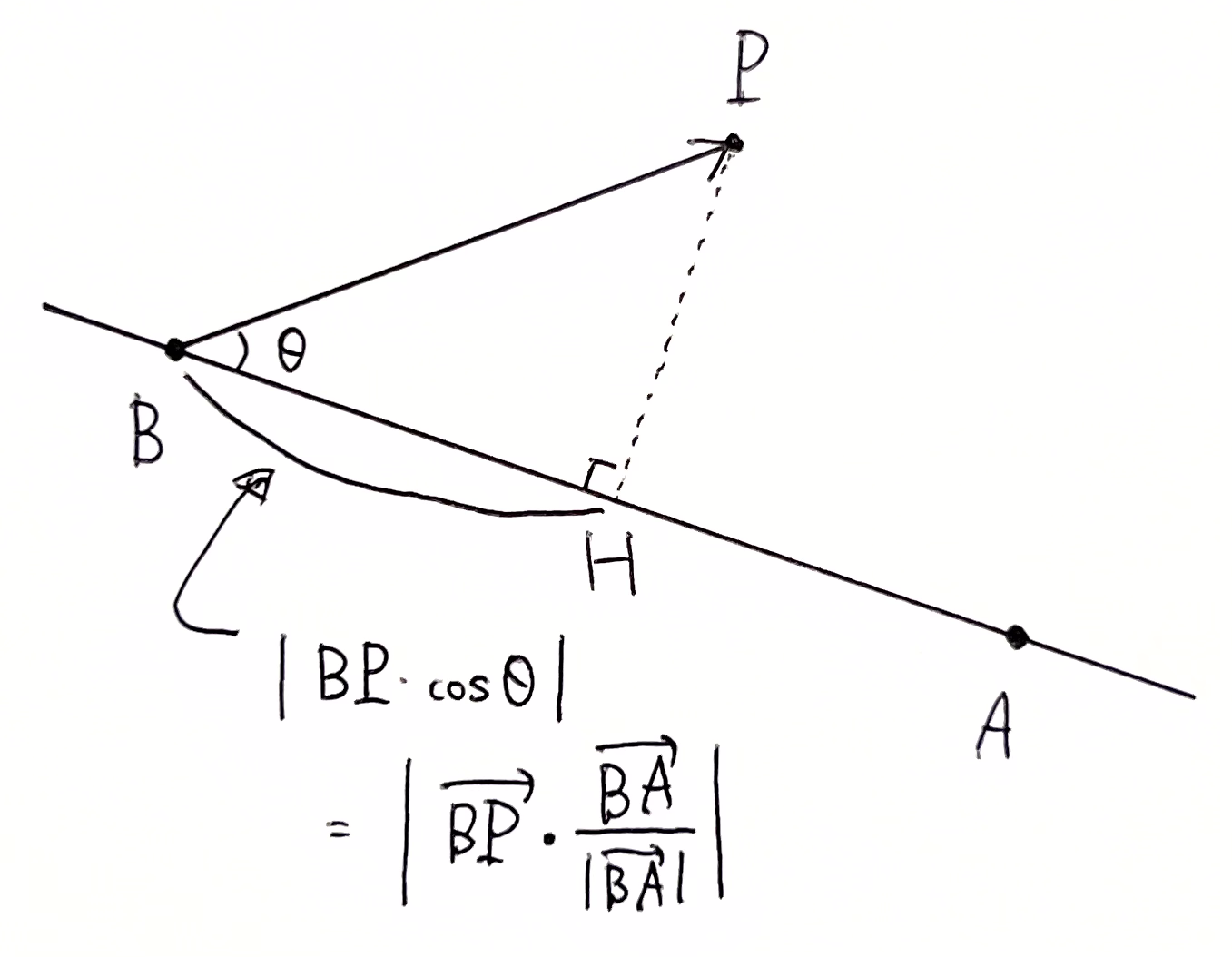
よって、三平方の定理より
\begin{align}
{\rm PB}^2-{\rm PH}^2
=\left(\overrightarrow{\rm BP}\cdot\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}\right)^2
\end{align}となる。
同様に、点 \({\rm P}\) から直線 \({\rm BC}\) に下ろした垂線の足を \({\rm I}\) とする。直線 \({\rm BC}\) の方向ベクトルとして大きさが \(1\) の \(\displaystyle \frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}\) を考えると
\begin{align}
{\rm PB}^2-{\rm PI}^2
=\left(\overrightarrow{\rm BP}\cdot\frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}\right)^2
\end{align}となる。
条件より \({\rm PH}={\rm PI}\) である。よって、
\begin{align}
\overrightarrow{\rm BP}\cdot\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}&=\pm\left(\overrightarrow{\rm BP}\cdot\frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}\right)
\end{align}すなわち
\begin{align}
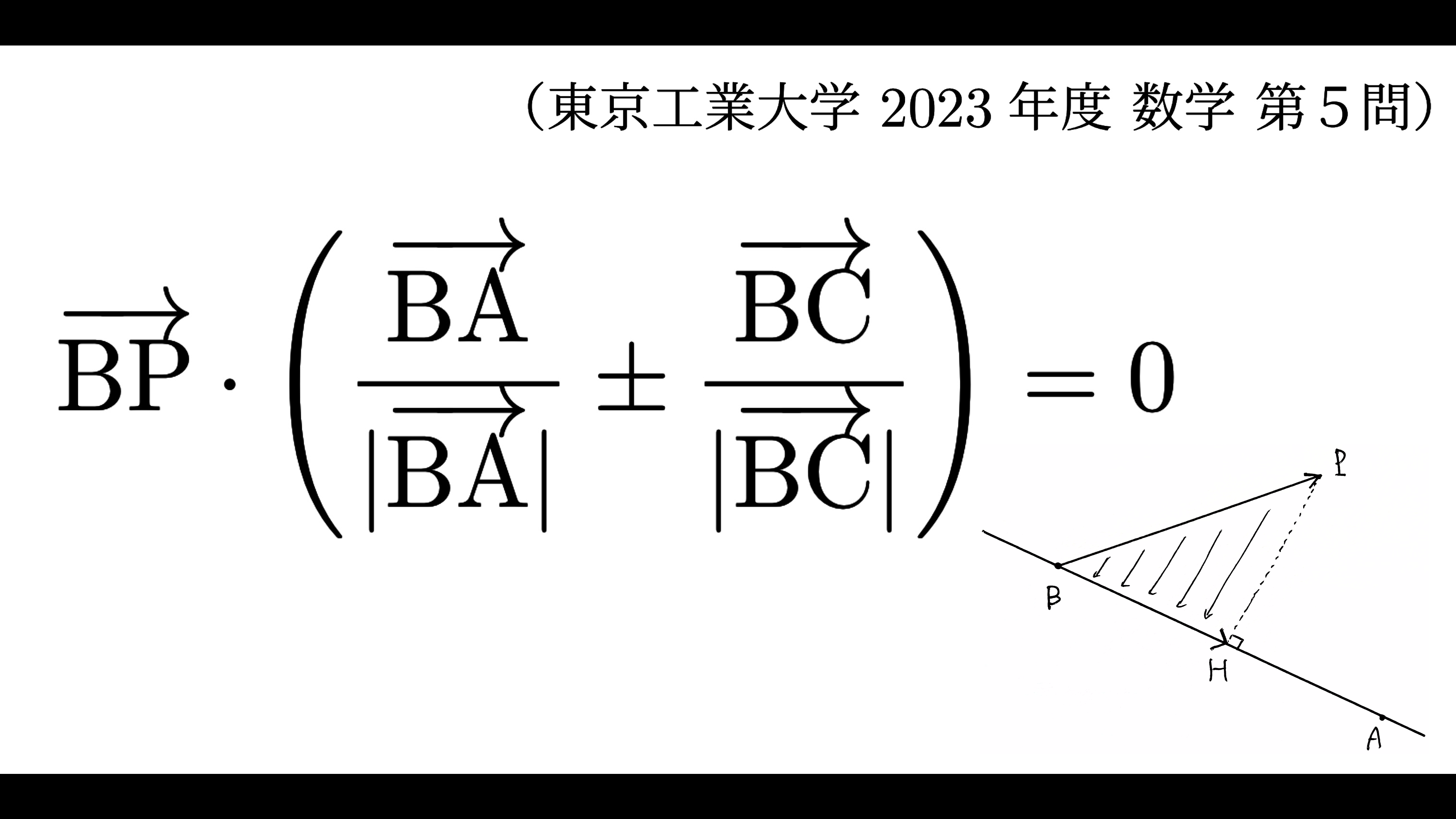
\overrightarrow{\rm BP}\cdot\left(\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}\pm\frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}\right)=0\tag{a}
\end{align}が成り立つ。
今、
\begin{align}
\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|}\pm\frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}
=\frac{1}{\sqrt{2}}\left(\begin{array}{c}-1\\-1\\-2\end{array}\right), \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\-1\\0\end{array}\right)
\end{align}
であるので、\({\rm P}(x,y,z)\) とおくと、(a)より $$-(x-1)-(y-1)-2(z-1)=0$$ または $$(x-1)-(y-1)=0$$ が成り立つ。
よって、求める図形は \(2\) 平面
\begin{gather}
x+y+2z-4=0,\tag{b1}\\
x-y=0\tag{b2}
\end{gather}を合わせた図形である。
(2)
点 \({\rm P}(x,y,z)\) が \(2\) 直線 \({\rm BC}\),\({\rm CD}\) から等距離であるための条件について
\begin{align}
\frac{\overrightarrow{\rm CB}}{|\overrightarrow{\rm CB}|}\pm\frac{\overrightarrow{\rm CD}}{|\overrightarrow{\rm CD}|}
=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\-1\\2\end{array}\right), \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\1\\0\end{array}\right)
\end{align}
であるので、(1)と同様に \(\overrightarrow{\rm CP}\) との内積を考えると $$(x+1)-(y-1)+2(z+1)=0$$ または $$(x+1)+(y-1)=0$$ となる。すなわち、
\begin{gather}
x-y+2z+4=0\tag{c1}
\end{gather}または
\begin{gather}
x+y=0\tag{c2}
\end{gather}である。
点 \({\rm P}(x,y,z)\) が \(2\) 直線 \({\rm CD}\),\({\rm DA}\) から等距離であるための条件について
\begin{align}
\frac{\overrightarrow{\rm DC}}{|\overrightarrow{\rm DC}|}\pm\frac{\overrightarrow{\rm DA}}{|\overrightarrow{\rm DA}|}
=\frac{1}{\sqrt{2}}\left(\begin{array}{c}\pm\sqrt{2}\\1\\-1\end{array}\right)
\end{align}であるので、(1)と同様に \(\overrightarrow{\rm DP}\) との内積を考えると
\begin{gather}
\pm\sqrt{2}(x+1)+y-z=0\tag{d}
\end{gather}である。
さて、直線 \({\rm DA}\) は \(x\) 軸なので、点 \({\rm P}(x,y,z)\) との距離 \(r\) は $$r=\sqrt{y^2+z^2}$$ と書ける。よって、
- (b1)かつ(c1)のとき $$x=-2z\ かつ\ y=4$$ なので、(d) より \(z=\pm\sqrt{2}\) である。よって \(r=3\sqrt{2}\) となる。
- (b1)かつ(c2)のとき $$x=-y\ かつ\ z=2$$ なので、(d) より \(y=\pm\sqrt{2}\) である。よって \(r=\sqrt{6}\) となる。
- (b2)かつ(c1)のとき $$x=y\ かつ\ z=-2$$ なので、(d) より \(x=\pm\sqrt{2}\) である。よって \(r=\sqrt{6}\) となる。
- (b2)かつ(c2)のとき \(x=y=0\) なので、(d) より \(z=\pm\sqrt{2}\) である。よって \(r=\sqrt{2}\) となる。
以上より、求める中心 \((x,y,z)\) と半径 \(r\) の組は
- 中心 \((\pm2\sqrt{2},4,\mp\sqrt{2})\),半径 \(3\sqrt{2}\)
- 中心 \((\pm\sqrt{2},\mp\sqrt{2},2)\),半径 \(\sqrt{6}\)
- 中心 \((\pm\sqrt{2},\pm\sqrt{2},-2)\),半径 \(\sqrt{6}\)
- 中心 \((0,0,\pm\sqrt{2})\),半径 \(\sqrt{2}\)
である。但し、それぞれ複号同順である。
考察と感想

今回は、複数の直線から等距離にある点の集まりに関する考察です。
この問題を解くときに抱いたのが「平面上なら中学校で作図してるな」という感想です。(1)のように、交わる \(2\) 直線から等距離にある点の集まりは、平面上なら角の二等分線を \(2\) 本引けば良いですね。この問題では「空間」ですが、\(3\) 点 \({\rm A}\),\({\rm B}\),\({\rm C}\) を含む平面上での角の二等分線 \(2\) 本は図形に含まれるだろうと予測できます。
直線 \({\rm AB}\) の方向ベクトル \(\overrightarrow{a}\) と直線 \({\rm BC}\) の方向ベクトル \(\overrightarrow{c}\) を、大きさが等しくなるように設定します。今回の解答で言うと
\begin{align}
\overrightarrow{a}&=\frac{\overrightarrow{\rm BA}}{|\overrightarrow{\rm BA}|},&
\overrightarrow{c}&=\frac{\overrightarrow{\rm BC}}{|\overrightarrow{\rm BC}|}
\end{align}とすると、\(|\overrightarrow{a}|=|\overrightarrow{c}|=1\) ですね。ここから、コンパスのイメージで、角の二等分線として \(\overrightarrow{a}\pm\overrightarrow{c}\) を得ます。
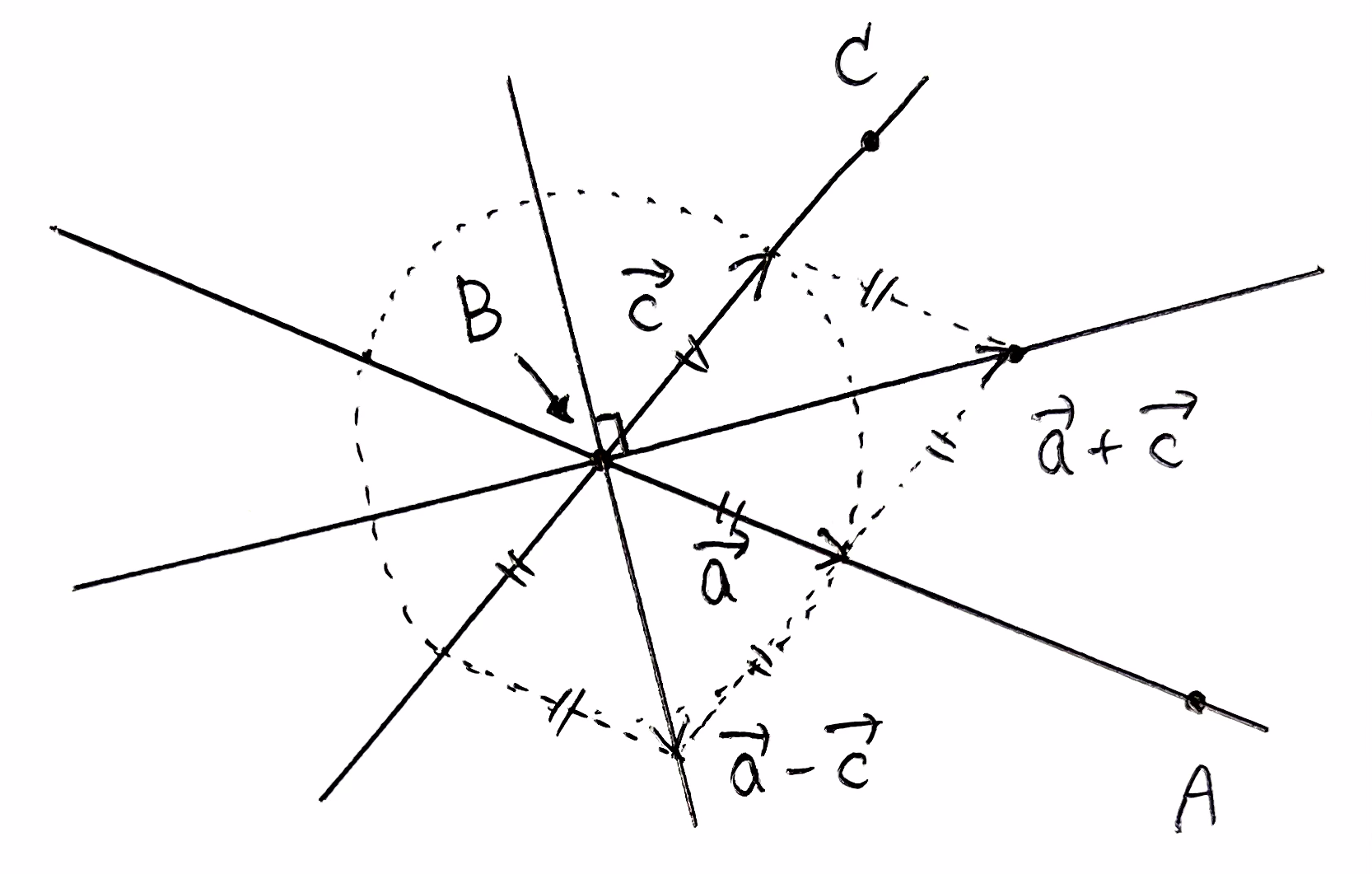
今回のように「空間」の場合は、この \(2\) 直線では不十分です。
そこで、この角の二等分線が直交することに着目します。直交することは図形的にもわかりますし、方向ベクトルの内積をとっても
\begin{align}
(\overrightarrow{a}+\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})
&=|\overrightarrow{a}|^2-|\overrightarrow{c}|^2\\
&=1^2-1^2\\
&=0
\end{align}となることがわかります。
つまり、点 \({\rm B}\) を通ることを前提とすれば
- \(\overrightarrow{a}-\overrightarrow{c}\) を方向ベクトルとする直線は、
平面上で \(\overrightarrow{a}+\overrightarrow{c}\) に直交するもの - \(\overrightarrow{a}+\overrightarrow{c}\) を方向ベクトルとする直線は、
平面上で \(\overrightarrow{a}-\overrightarrow{c}\) に直交するもの
と言えます。この表現で「平面」から「空間」に持ってゆくとどうなるでしょうか。
- \(\overrightarrow{\rm BP}\) が \(\overrightarrow{a}+\overrightarrow{c}\) に直交するような点 \({\rm P}\) の集まりが平面 (b1)
- \(\overrightarrow{\rm BP}\) が \(\overrightarrow{a}-\overrightarrow{c}\) に直交するような点 \({\rm P}\) の集まりが平面 (b2)
となっています。
点 \({\rm B}\) を通り、\(\overrightarrow{a}\pm\overrightarrow{c}\) を 法線ベクトル に持つような “2次元の空間” (平面)たちになっていますね。

コメント