みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の不定積分
\begin{align}
I_n(x)&=\int \sin^n x\,dx,\\
J_n(x)&=\int \cos^n x\,dx
\end{align}
を考える。但し、\(\sin^0 x\),\(\cos^0 x\) は共に \(1\) とする。
(1)\(I_0(x)\) と \(I_1(x)\) を求めよ。
(2)\(n\geq2\) に対して \(I_n(x)\) を \(I_{n-2}(x)\) で表すことで、\(I_4(x)\) と \(I_5(x)\) を求めよ。
(3)\(J_n(x)\) を \(\displaystyle I_n\left(\frac{\pi}{2}-x\right)\) を用いて表せ。
その他の例題は以下のリンクを参照してください。
答え
(1)
\begin{gather}
I_0(x)=x+C_0
\end{gather}また
\begin{gather}
I_1(x)=-\cos x+C_1
\end{gather}
但し、\(C_0\) と \(C_1\) は積分定数とする。
(2)
\begin{gather}
I_4(x)=\frac{3}{8}x-\frac{3}{8}\cos x\sin x-\frac{1}{4}\cos x\sin^3x+C_4
\end{gather}
また
\begin{align}
I_5(x)
&=-\frac{8}{15}\cos x-\frac{4}{15}\cos x\sin^2x-\frac{1}{5}\cos x\sin^4x+C_5
\end{align}
但し、\(C_4\) と \(C_5\) は積分定数とする。
(3)\(\displaystyle J_n(x)=-I_n\left(\frac{\pi}{2}-x\right)\)
解説


\(I_0(x)\) と \(I_1(x)\) を求める。
まず、\(\sin^0 x=1\) と約束していたので、\(C_0\) を積分定数とすると
\begin{align}
I_0(x)
=\int 1\,dx
=x+C_0
\end{align}となります。
また、\(C_1\) を積分定数とすると
\begin{align}
I_1(x)
=\int \sin x\,dx
=-\cos x+C_1
\end{align}となります。
\(I_n(x)\) の漸化式を求める。
\(n\geq2\) であることを用いて部分積分を行います。
\begin{align}
I_n(x)
&=\int \sin x\sin^{n-1}x\,dx\\
&=(-\cos x)\sin^{n-1}x-\int(-\cos x)\{(n-1)\cos x\sin^{n-2}x\}\,dx\\
&=-\cos x\sin^{n-1}x+(n-1)\int \cos^2x\sin^{n-2}x\,dx\\
&=-\cos x\sin^{n-1}x+(n-1)\int (1-\sin^2x)\sin^{n-2}x\,dx\\
&=-\cos x\sin^{n-1}x+(n-1)(I_{n-2}(x)-I_n(x))
\end{align}
これを \(I_n(x)\) について解くことで
\begin{align}
I_n(x)=\frac{n-1}{n}I_{n-2}(x)-\frac{1}{n}\cos x\sin^{n-1}x
\end{align}を得ます。
\(n=4\) とすると
漸化式を繰り返し用いることで
\begin{align}
I_4(x)
&=\frac{3}{4}I_{2}(x)-\frac{1}{4}\cos x\sin^{3}x\\
&=\frac{3}{4}\left(\frac{1}{2}I_{0}(x)-\frac{1}{2}\cos x\sin x\right)-\frac{1}{4}\cos x\sin^{3}x\\
&=\frac{3}{8}I_{0}(x)-\frac{3}{8}\cos x\sin x-\frac{1}{4}\cos x\sin^{3}x
\end{align}
となります。\(I_{0}(x)\) は既に求めていたので、\(C_4\) を積分定数とすると
\begin{align}
I_4(x)
&=\frac{3}{8}x-\frac{3}{8}\cos x\sin x-\frac{1}{4}\cos x\sin^{3}x+C_4
\end{align}
となります。
\(n=5\) とすると
漸化式を繰り返し用いることで
\begin{align}
I_5(x)
&=\frac{4}{5}I_{3}(x)-\frac{1}{5}\cos x\sin^{4}x\\
&=\frac{4}{5}\left(\frac{2}{3}I_{1}(x)-\frac{1}{3}\cos x\sin^2x\right)-\frac{1}{5}\cos x\sin^{4}x\\
&=\frac{8}{15}I_{0}(x)-\frac{4}{15}\cos x\sin x-\frac{1}{5}\cos x\sin^{4}x
\end{align}
となります。\(I_{1}(x)\) は既に求めていたので、\(C_5\) を積分定数とすると
\begin{align}
I_5(x)
&=-\frac{8}{15}\cos x-\frac{4}{15}\cos x\sin^2x-\frac{1}{5}\cos x\sin^4x+C_5
\end{align}
となります。
\(I_n(x)\) と \(J_n(x)\) の関係とは。
一般に \(\displaystyle \sin\left(\frac{\pi}{2}-x\right)=\cos x\) が成り立つことが関連しています。
\(\displaystyle y=\frac{\pi}{2}-x\) とおくと \(\displaystyle dy=-dx\) であるので
\begin{align}
I_n(y)
&=\int \sin^n y\,dy\\
&=\int \sin^n\left(\frac{\pi}{2}-x\right)(-1)\,dx\\
&=-\int \cos^n x\,dx\\
&=-J_n(x)
\end{align}すなわち
\begin{align}
J_n(x)=-I_n\left(\frac{\pi}{2}-x\right)
\end{align}を得ます。
最後に


今回は、不定積分 による関数の列 \(\{I_n(x)\}\) を考えました。
それを 定積分 にすると、区間に応じて数列 \(\{I_n\}\) を得られますね。
その区間の設定として例えば \(\displaystyle \left[0,\frac{\pi}{2}\right]\) を採用すると
- 漸化式 $$I_n(x)=\frac{n-1}{n}I_{n-2}(x)-\frac{1}{n}\cos x\sin^{n-1}x$$ において \(\cos x\sin x\) を含む項は両端の値の代入によって必ず \(0\) になる。
- (3)で示した関係式と同様にして $$\int_0^{\frac{\pi}{2}} \sin^n x\,dx=\int_0^{\frac{\pi}{2}} \cos^n x\,dx$$ が成り立つ。
ことが言えます。
この数列
\begin{align}
I_n&=\int_0^{\frac{\pi}{2}} \sin^n x\,dx,\\
J_n&=\int_0^{\frac{\pi}{2}} \cos^n x\,dx
\end{align}に関しては、以下の記事で扱っています。
関連 : 数学IIICカテゴリー
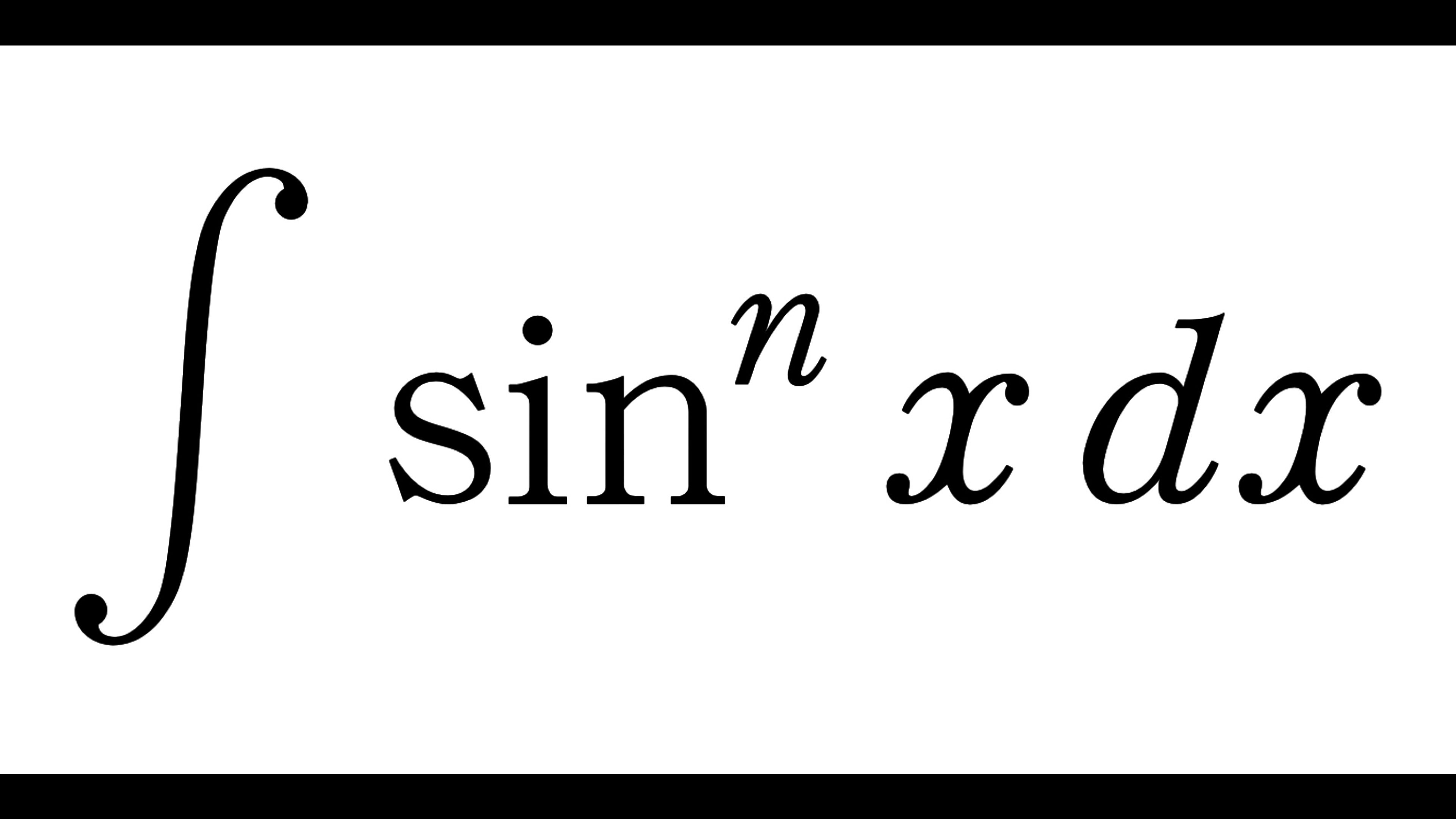
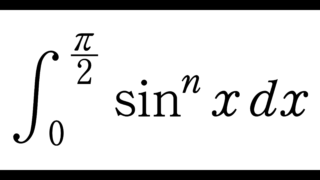
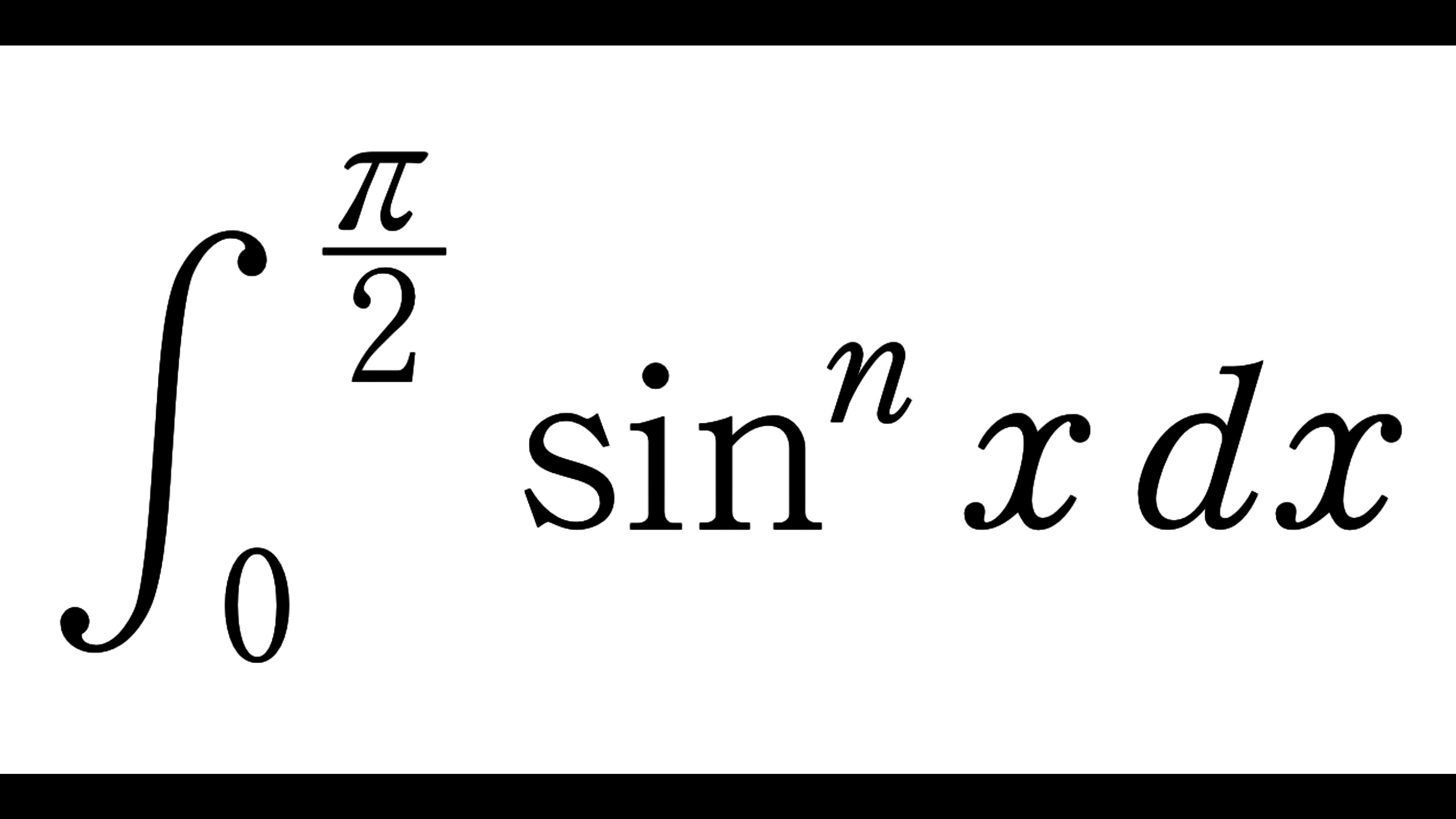
コメント