みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の不定積分
\begin{align}
K_n(x)&=\int \tan^n x\,dx
\end{align}
を考える。但し、\(\tan^0 x=1\) とする。
(1)\(K_0(x)\) と \(K_1(x)\) を求めよ。
(2)\(n\geq2\) に対して \(K_n(x)\) を \(K_{n-2}(x)\) で表すことで、\(K_4(x)\) と \(K_5(x)\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)
\begin{gather}
K_0(x)=x+C_0
\end{gather}また
\begin{gather}
K_1(x)=-\log|\cos x|+C_1
\end{gather}
但し、\(C_0\) と \(C_1\) は積分定数とする。
(2)
\begin{gather}
K_4(x)=\frac{1}{3}\tan^3x-\tan x+x+C_4
\end{gather}また
\begin{align}
K_5(x)=\frac{1}{4}\tan^4x-\frac{1}{2}\tan^2x-\log|\cos x|+C_5
\end{align}
但し、\(C_4\) と \(C_5\) は積分定数とする。
解説

\(K_0(x)\) と \(K_1(x)\) を求める。
まず、\(\tan^0 x=1\) と約束していたので、\(C_0\) を積分定数とすると
\begin{align}
K_0(x)
=\int 1\,dx
=x+C_0
\end{align}となります。
また、\(C_1\) を積分定数とすると
\begin{align}
K_1(x)
&=\int\frac{\sin x}{\cos x}\,dx\\
&=-\log|\cos x|+C_1
\end{align}となります。
\(K_n(x)\) の漸化式を求める。
\(n\geq2\) であることを用いて変形をすることで
\begin{align}
K_n(x)
&=\int \tan^2x\tan^{n-2}x\,dx\\
&=\int\left(\frac{1}{\cos^2 x}-1\right)\tan^{n-2}x\,dx\\
&=\int\frac{1}{\cos^2 x}\tan^{n-2}x\,dx-\int\tan^{n-2}x\,dx\\
&=\frac{1}{n-1}\tan^{n-1}x-K_{n-2}(x)
\end{align}を得ます。
\(n=4\) とすると
漸化式を繰り返し用いることで
\begin{align}
K_4(x)
&=\frac{1}{3}\tan^3x-K_2(x)\\
&=\frac{1}{3}\tan^3x-\tan x+K_0(x)
\end{align}
となります。\(K_{0}(x)\) は既に求めていたので、\(C_4\) を積分定数とすると
\begin{align}
K_4(x)
&=\frac{1}{3}\tan^3x-\tan x+x+C_4
\end{align}
となります。
\(n=5\) とすると
漸化式を繰り返し用いることで
\begin{align}
K_5(x)
&=\frac{1}{4}\tan^{4}x-K_{3}(x)\\
&=\frac{1}{4}\tan^{4}x-\frac{1}{2}\tan^{2}x+K_{1}(x)
\end{align}
となります。\(K_{1}(x)\) は既に求めていたので、\(C_5\) を積分定数とすると
\begin{align}
K_5(x)=\frac{1}{4}\tan^{4}x-\frac{1}{2}\tan^{2}x-\log|\cos x|+C_5
\end{align}
となります。
最後に

今回は、不定積分 による関数の列 \(\{K_n(x)\}\) を考えました。
それを 定積分 にすると、区間に応じて数列 \(\{K_n\}\) を得られますね。
その区間の設定として例えば \(\displaystyle \left[0,\frac{\pi}{4}\right]\) を採用すると
- 漸化式 $$K_n(x)=\frac{1}{n-1}\tan^{n-1}x-K_{n-2}(x)$$ において \(\tan x\) を含む項は、積分区間の両端の値を代入することで \(0\) または \(1\) になる。
ことが言えます。
この数列
\begin{align}
K_n=\int_0^{\frac{\pi}{4}} \tan^n x\,dx
\end{align}に関しては、以下の記事で扱っています。
関連 : 数学IIICカテゴリー
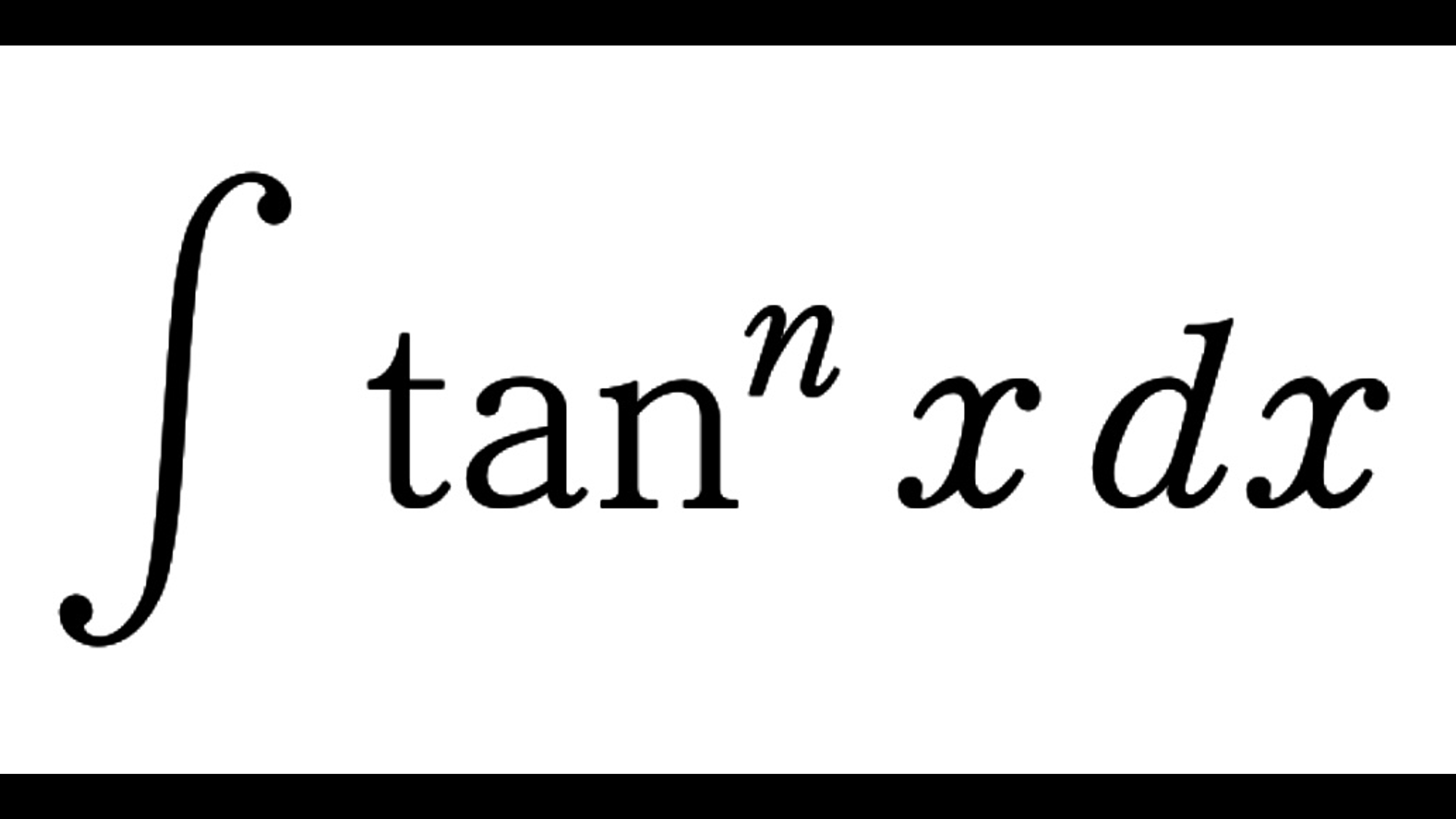
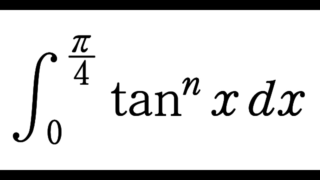
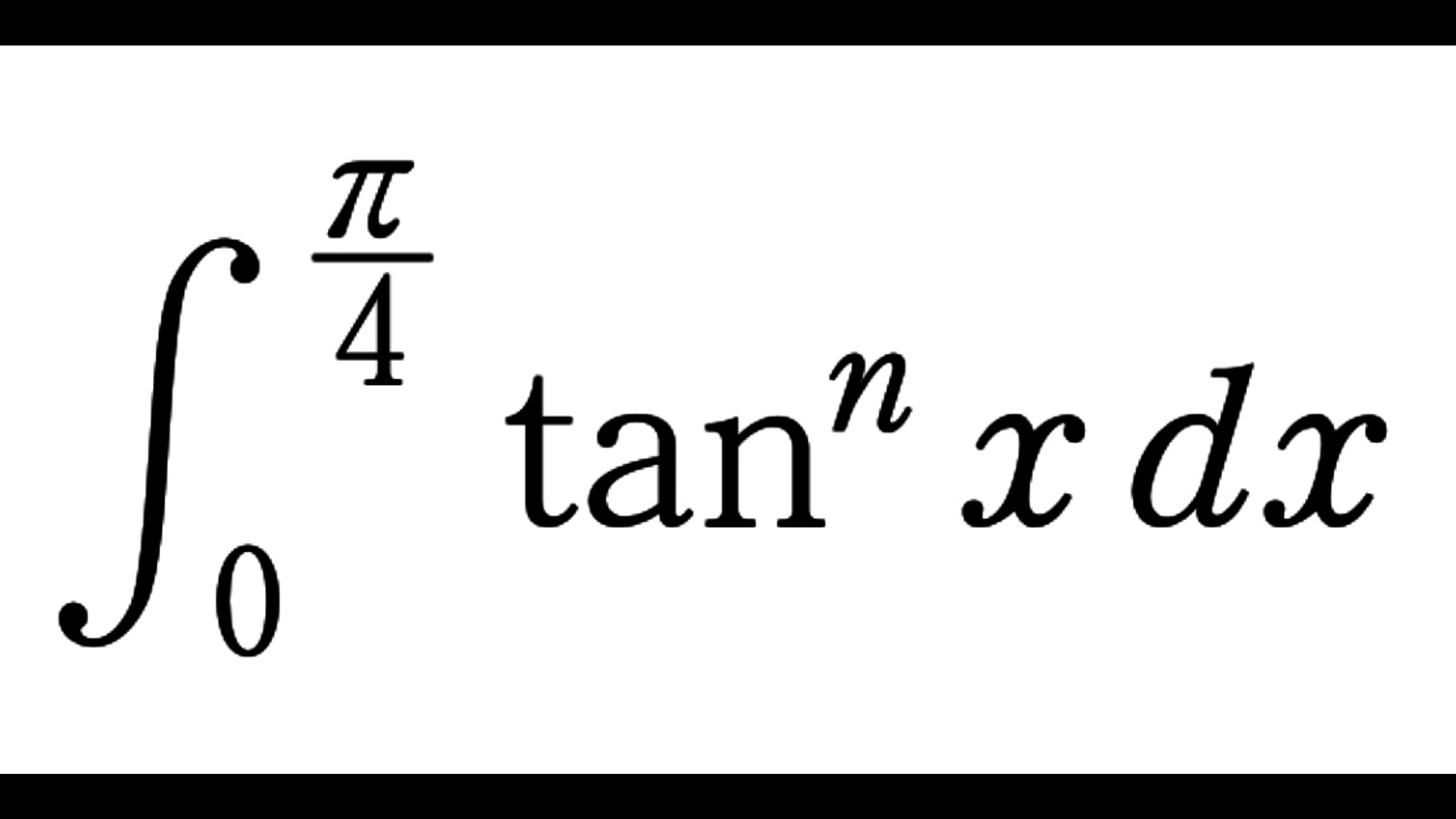
コメント