みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の定積分
\begin{align}
I_n&=\int_0^{\frac{\pi}{2}} \sin^n x\,dx,\\
J_n&=\int_0^{\frac{\pi}{2}} \cos^n x\,dx
\end{align}
を考える。但し、\(\sin^0 x\),\(\cos^0 x\) は共に \(1\) とする。
(1)\(I_0\) と \(I_1\) を求めよ。
(2)\(n\geq2\) に対して \(I_n\) を \(I_{n-2}\) で表すことで、\(I_6\) と \(I_7\) を求めよ。
(3)\(n\geq2\) に対して \(I_n\) を求めよ。
(4)\(J_n\) を \(I_n\) を用いて表せ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle I_0=\frac{\pi}{2}\),\(\displaystyle I_1=1\)
(2)\(\displaystyle I_6=\frac{5}{32}\pi\),\(\displaystyle I_7=\frac{16}{35}\)
(3)\(n\) が偶数のとき
\begin{align}
I_n=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}
\end{align}
\(n\) が奇数のとき
\begin{align}
I_n=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{4}{5}\times\frac{2}{3}\times1
\end{align}
(4)\(J_n=I_n\)
解説

\(I_0\) と \(I_1\) を求める。
まず、\(\sin^0 x=1\) と約束していたので
\begin{align}
I_0
=\int_0^{\frac{\pi}{2}} 1\,dx
=\frac{\pi}{2}
\end{align}となります。
また、
\begin{align}
I_1
=\int_0^{\frac{\pi}{2}}\sin x\,dx
=\left[-\cos x\right]_0^{\frac{\pi}{2}}
=1
\end{align}となります。
\(I_n\) の漸化式を求める。
\(n\geq2\) であることを用いて部分積分を行います。
\begin{align}
I_n
&=\int_0^{\frac{\pi}{2}}\sin x\sin^{n-1}x\,dx\\
&=\left[(-\cos x)\sin^{n-1}x\right]_0^{\frac{\pi}{2}}-\int_0^{\frac{\pi}{2}}(-\cos x)\{(n-1)\cos x\sin^{n-2}x\}\,dx\\
&=0+(n-1)\int_0^{\frac{\pi}{2}}\cos^2x\sin^{n-2}x\,dx\\
&=(n-1)\int_0^{\frac{\pi}{2}}(1-\sin^2x)\sin^{n-2}x\,dx\\
&=(n-1)(I_{n-2}-I_n)
\end{align}
これを \(I_n\) について解くことで
\begin{align}
I_n=\frac{n-1}{n}I_{n-2}
\end{align}を得ます。
\(n=6\) とすると
漸化式を繰り返し用いることで
\begin{align}
I_6
&=\frac{5}{6}\times I_4\\
&=\frac{5}{6}\times\frac{3}{4}\times I_2\\
&=\frac{5}{6}\times\frac{3}{4}\times\frac{1}{2}\times I_0
\end{align}
となります。\(I_0\) は既に求めていたので
\begin{align}
I_6=\frac{5}{6}\times\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}=\frac{5}{32}\pi
\end{align}
となります。
\(n=7\) とすると
漸化式を繰り返し用いることで
\begin{align}
I_7
&=\frac{6}{7}\times I_5\\
&=\frac{6}{7}\times\frac{4}{5}\times I_3\\
&=\frac{6}{7}\times\frac{4}{5}\times\frac{2}{3}\times I_1
\end{align}
となります。\(I_1\) は既に求めていたので
\begin{align}
I_7=\frac{6}{7}\times\frac{4}{5}\times\frac{2}{3}\times1=\frac{16}{35}
\end{align}
となります。
\(I_n\) の一般項を求める。
\(I_6\) や \(I_7\) を求めたときと同様に、\(n\) の偶奇によって場合分けをして漸化式を用います。
\(n\) が偶数のとき
\begin{align}
I_n
&=\frac{n-1}{n}\times I_{n-2}\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times I_{n-4}\\
&\qquad\ \ \vdots\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{3}{4}\times\frac{1}{2}\times I_0\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}
\end{align}
\(n\) が奇数のとき
\begin{align}
I_n
&=\frac{n-1}{n}\times I_{n-2}\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times I_{n-4}\\
&\qquad\ \ \vdots\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{4}{5}\times\frac{2}{3}\times I_1\\
&=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac{4}{5}\times\frac{2}{3}\times1
\end{align}
\(I_n\) と \(J_n\) の関係とは。
一般に \(\displaystyle \sin\left(\frac{\pi}{2}-x\right)=\cos x\) が成り立つことが関連しています。
\(\displaystyle x=\frac{\pi}{2}-y\) とおくと \(\displaystyle dx=-dy\) であるので
\begin{align}
J_n
&=\int_0^{\frac{\pi}{2}} \cos^n x\,dx\\
&=\int_{\frac{\pi}{2}}^0 \cos^n\left(\frac{\pi}{2}-y\right)(-1)\,dy\\
&=\int_0^{\frac{\pi}{2}} \sin^ny\,dy\\
&=I_n
\end{align}を得ます。
最後に

(3)で求めた数列 \(\{I_n\}\) の一般項では、階乗ではないですが、一個飛ばしの整数の積が現れました。
一般的な高校数学では扱われませんが、二重階乗 というもので簡潔に表現することができます。
正の整数 \(n\) に対して
\begin{align}
n!!=\begin{cases}
n(n-2)\cdots\times4\times2&(n:偶数)\\
n(n-2)\cdots\times3\times1&(n:奇数)
\end{cases}
\end{align}と定義します。また、
\begin{align}
0!!&=1,&
(-1)!!&=1
\end{align}と約束します。
この記号により、\(0\) 以上の整数 \(n\) に対して
\begin{align}
I_n=\begin{cases}
\displaystyle \frac{(n-1)!!}{n!!}\times\frac{\pi}{2}&(n:偶数)\\[5pt]
\displaystyle \frac{(n-1)!!}{n!!}&(n:奇数)
\end{cases}
\end{align}と書くことができます。
この積分は「ウォリス積分」と呼ばれることがあります。
関連 : 数学IIICカテゴリー
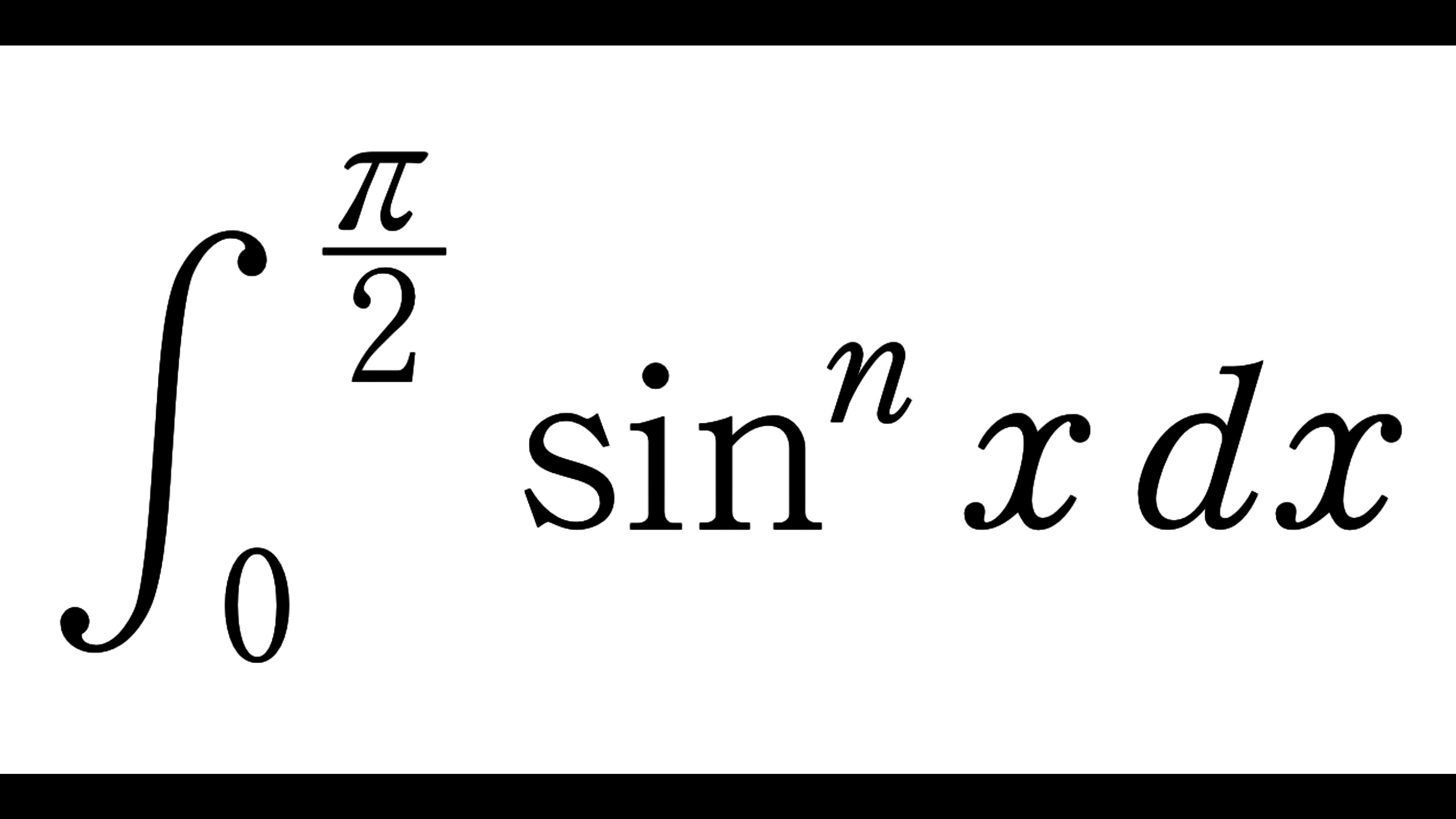

コメント