みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の定積分
\begin{align}
K_n&=\int_0^{\frac{\pi}{4}} \tan^n x\,dx
\end{align}
を考える。但し、\(\tan^0 x=1\) とする。
(1)\(K_0\) と \(K_1\) を求めよ。
(2)\(n\geq2\) に対して \(K_n\) を \(K_{n-2}\) で表すことで、\(K_6\) と \(K_7\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle K_0=\frac{\pi}{4}\),\(\displaystyle K_1=\frac{1}{2}\log2\)
(2)\(\displaystyle K_6=\frac{13}{15}-\frac{\pi}{4}\),\(\displaystyle K_7=\frac{5}{12}-\frac{1}{2}\log2\)
解説

\(K_0\) と \(K_1\) を求める。
まず、\(\tan^0 x=1\) と約束していたので
\begin{align}
K_0
=\int_0^{\frac{\pi}{4}} 1\,dx
=\frac{\pi}{4}
\end{align}となります。
また、
\begin{align}
K_1
&=\int_0^{\frac{\pi}{4}}\frac{\sin x}{\cos x}\,dx\\
&=\left[-\log|\cos x|\right]_0^{\frac{\pi}{4}}\\
&=\frac{1}{2}\log2
\end{align}となります。
\(K_n\) の漸化式を求める。
\(n\geq2\) であることを用いて部分積分を行います。
\begin{align}
K_n
&=\int_0^{\frac{\pi}{4}}\tan^2 x\tan^{n-2}x\,dx\\
&=\int_0^{\frac{\pi}{4}}\left(\frac{1}{\cos^2 x}-1\right)\tan^{n-2}x\,dx\\
&=\int_0^{\frac{\pi}{4}}\frac{1}{\cos^2 x}\tan^{n-2}x\,dx-\int_0^{\frac{\pi}{4}}\tan^{n-2}x\,dx\\
&=\left[\frac{1}{n-1}\tan^{n-1}x\right]_0^{\frac{\pi}{4}}-\int_0^{\frac{\pi}{4}}\tan^{n-2}x\,dx\\
&=\frac{1}{n-1}-K_{n-2}
\end{align}
を得ます。
\(n=6\) とすると
漸化式を繰り返し用いることで
\begin{align}
K_6
&=\frac{1}{5}-K_4\\
&=\frac{1}{5}-\frac{1}{3}+K_2\\
&=\frac{1}{5}-\frac{1}{3}+\frac{1}{1}-K_0
\end{align}
となります。\(K_0\) は既に求めていたので
\begin{align}
K_6
&=\frac{1}{5}-\frac{1}{3}+\frac{1}{1}-\frac{\pi}{4}\\
&=\frac{13}{15}-\frac{\pi}{4}
\end{align}
となります。
\(n=7\) とすると
漸化式を繰り返し用いることで
\begin{align}
K_7
&=\frac{1}{6}-K_5\\
&=\frac{1}{6}-\frac{1}{4}+K_3\\
&=\frac{1}{6}-\frac{1}{4}+\frac{1}{2}-K_1
\end{align}
となります。\(K_1\) は既に求めていたので
\begin{align}
K_7
&=\frac{1}{6}-\frac{1}{4}+\frac{1}{2}-\frac{1}{2}\log2\\
&=\frac{5}{12}-\frac{1}{2}\log2
\end{align}
となります。
最後に

さて、数列 \(\{K_n\}\) の 一般項 が明示的に書けるか考えてみましょう。
\(K_6\) や \(K_7\) を求めたときと同様に、正の整数 \(n\) の偶奇によって場合分けをし、漸化式を用います。
\(n=2m\) のとき
例えば
\begin{align}
K_{50}
&=\frac{1}{49}-\frac{1}{47}+\cdots-\frac{1}{3}+1-\frac{\pi}{2}
\end{align}
であったり
\begin{align}
K_{100}
&=\frac{1}{99}-\frac{1}{97}+\cdots+\frac{1}{3}-1+\frac{\pi}{2}
\end{align}
となります。
一般には、
\begin{align}
K_{2m}
&=\frac{1}{2m-1}-\frac{1}{2m-3}+\cdots+\frac{(-1)^{m-2}}{3}+\frac{(-1)^{m-1}}{1}+(-1)^m\frac{\pi}{2}
\end{align}
と書けます。
\(n=2m+1\) のとき
例えば
\begin{align}
K_{51}
&=\frac{1}{50}-\frac{1}{48}+\cdots-\frac{1}{4}+\frac{1}{2}-\frac{1}{2}\log2
\end{align}
であったり
\begin{align}
K_{101}
&=\frac{1}{100}-\frac{1}{98}+\cdots+\frac{1}{4}-\frac{1}{2}+\frac{1}{2}\log2
\end{align}
となります。
一般には、
\begin{align}
K_{2m+1}
&=\frac{1}{2m}-\frac{1}{2m-2}+\cdots+\frac{(-1)^{m-2}}{4}+\frac{(-1)^{m-1}}{2}+(-1)^m\frac{1}{2}\log2
\end{align}
と書けます。
関連 : 数学IIICカテゴリー
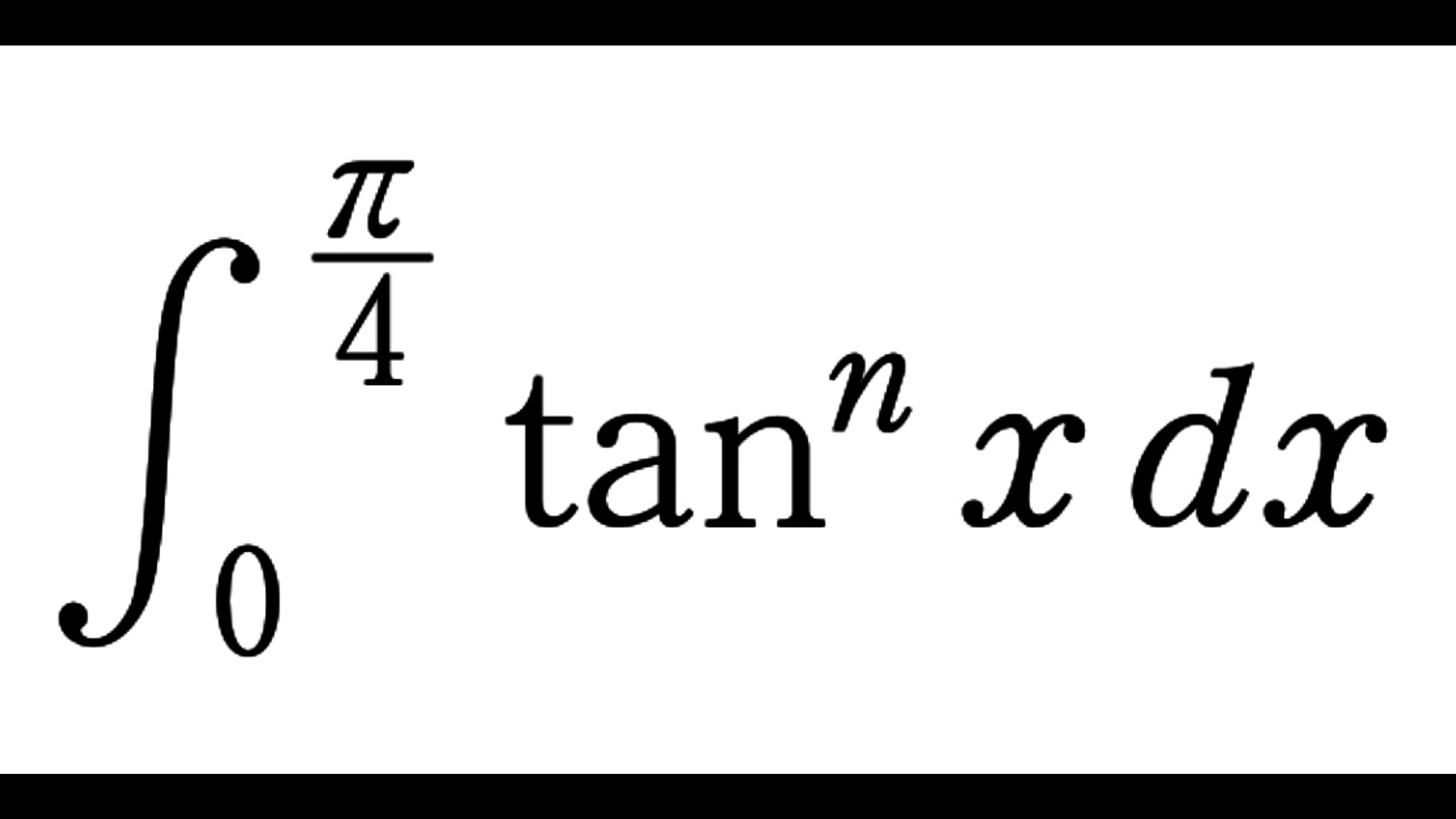
コメント