数学IIで習う 二項係数 $${}_{n}{\rm C}_{k}=\frac{n!}{k!(n-k)!}$$ について、今回は以下の「基本的な性質」を証明してゆきたいと思います。
他の公式は以下の リンク を参照してください。
基本的な性質

\({}_{n}{\rm C}_{k}={}_{n-1}{\rm C}_{k-1}+{}_{n-1}{\rm C}_{k}\)
$${}_{n}{\rm C}_{k}={}_{n-1}{\rm C}_{k-1}+{}_{n-1}{\rm C}_{k}$$
証明の一例
\begin{align}
&{}_{n-1}{\rm C}_{k-1}+{}_{n-1}{\rm C}_{k}\\
&\quad=\frac{(n-1)!}{(k-1)!\{(n-1)-(k-1)\}!}+\frac{(n-1)!}{k!\{(n-1)-k\}!}\\
&\quad=\frac{(n-1)!}{(k-1)!(n-k)!}+\frac{(n-1)!}{k!(n-k-1)!}\\
&\quad=\frac{(n-1)!}{k!(n-k)!}\left\{k+(n-k)\right\}\\
&\quad=\frac{(n-1)!}{k!(n-k)!}\times n\\
&\quad=\frac{n!}{k!(n-k)!}\\
&\quad={}_{n}{\rm C}_{k}
\end{align}
まず、\(1, 2, \cdots, n\) の中から \(k\) 個の数を選ぶときの選び方が \({}_{n}{\rm C}_{k}\) 通りです。このとき、
- 数「\(n\)」を選ぶ場合は \(1, 2, \cdots, n-1\) の中から \(k-1\) 個の数を選ぶことになり \({}_{n-1}{\rm C}_{k-1}\) 通り。
- 数「\(n\)」を選ばない場合は \(1, 2, \cdots, n-1\) の中から \(k\) 個の数を選ぶことになり \({}_{n-1}{\rm C}_{k}\) 通り。
この解釈より、計算なくして $${}_{n}{\rm C}_{k}={}_{n-1}{\rm C}_{k-1}+{}_{n-1}{\rm C}_{k}$$ を確認することができます。
これはパスカルの三角形を書くときのルールですね。
\({}_{n}{\rm C}_{k}={}_{n}{\rm C}_{n-k}\)
$${}_{n}{\rm C}_{k}={}_{n}{\rm C}_{n-k}$$
証明の一例
\begin{align}
{}_{n}{\rm C}_{n-k}
&=\frac{n!}{(n-k)!\{n-(n-k)\}!}\\
&=\frac{n!}{(n-k)!k!}\\
&={}_{n}{\rm C}_{k}
\end{align}
まず、\(1, 2, \cdots, n\) の中から \(k\) 個の数を選ぶときの選び方が \({}_{n}{\rm C}_{k}\) 通りでした。
その \(k\) 個を決めた瞬間、選ばれなかった \(n-k\) 個も同時に決定します。
\(1, 2, \cdots, n\) の中から \(n-k\) 個の数を選ぶときの選び方は \({}_{n}{\rm C}_{n-k}\) 通りなので $${}_{n}{\rm C}_{k}={}_{n}{\rm C}_{n-k}$$ を得ます。
これはパスカルの三角形が左右対称であることを意味します。
\({}_{n}{\rm C}_{k}=\frac{n}{k}{}_{n-1}{\rm C}_{k-1}\)
$${}_{n}{\rm C}_{k}=\frac{n}{k}{}_{n-1}{\rm C}_{k-1}$$
証明の一例
\begin{align}
{}_{n}{\rm C}_{k}
&=\frac{n!}{k!(n-k)!}\\
&=\frac{n}{k}\frac{(n-1)!}{(k-1)!(n-k)!}\\
&=\frac{n}{k}\frac{(n-1)!}{(k-1)!\{(n-1)-(k-1)\}!}\\
&=\frac{n}{k}{}_{n-1}{\rm C}_{k-1}
\end{align}
二項係数 \({}_{n}{\rm C}_{k}\) は、別の記号 \(\displaystyle \binom{n}{k}\) で表すこともあります。
この関係式は一見すると覚えにくいかもしれませんが、この表記を採用して $$\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}$$ と表すと、少し整って見えるかもしれません。
これは二項係数の和の計算で活躍します!
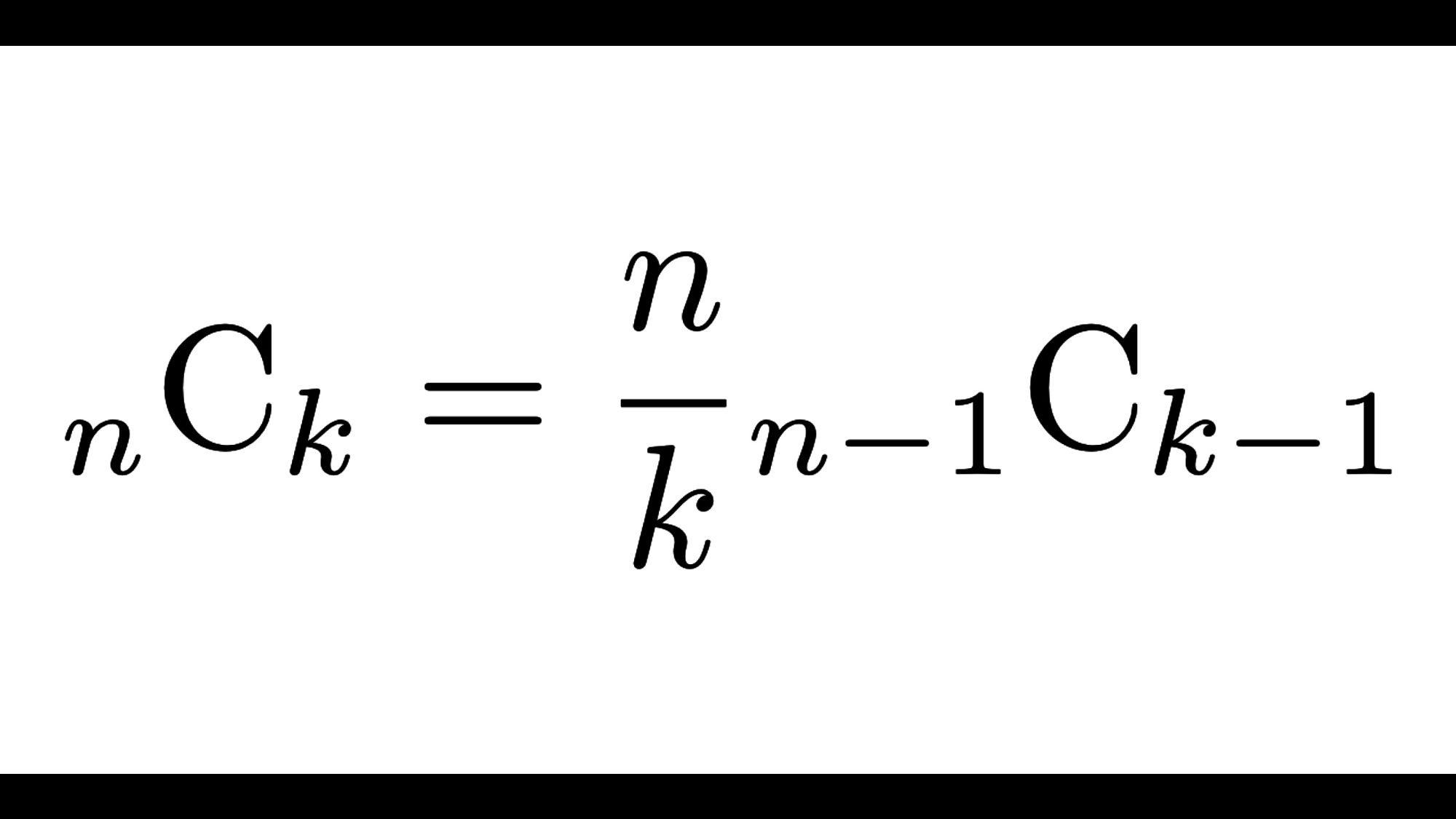
コメント