数学IIで習う 二項係数 \({}_{n}{\rm C}_{k}\) について、二項定理 より
\begin{align}
(1+x)^n=\sum_{k=0}^n{}_{n}{\rm C}_{k}x^k\tag{A}
\end{align}
となります。今回は、この式を中心に以下の「二項定理の利用」を扱ってゆきたいと思います。
※ \(x\) に値を代入してゆくので、\(n=0\) で成り立つものもありますが、基本的に \(n\geq1\) とします。
他の公式は以下の リンク を参照してください。
二項定理を用いた和の計算

\({}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^n {}_{n}{\rm C}_{k}=2^n$$
証明の一例
式 \(({\rm A})\) に \(x=1\) を代入することで $$\sum_{k=0}^n{}_{n}{\rm C}_{k}=(1+1)^n=2^n$$ を得る。
※ \(n=0\) のときも成り立つ。
左辺である \(\displaystyle \sum_{k=0}^n {}_{n}{\rm C}_{k}\) は、\(n\) 個の球から
- \(0\) 個選ぶときの場合の数
- \(1\) 個選ぶときの場合の数
- \(2\) 個選ぶときの場合の数 …
- \(n\) 個選ぶときの場合の数
の総和になります。つまり、\(n\) 個から球を選ぶときの全ての選び方を数えています。
一方、個数ではなく、各球に着目すると、各々が「選ばれる」もしくは「選ばれない」の \(2\) 通りがあります。これらは独立に考えられるので、$$2\times2\times2\times\cdots\times2=2^n$$ 通りとなります。
このように、別視点から同じものを数えることで確認することができることがあります。
\((-1)^k{}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^n (-1)^k{}_{n}{\rm C}_{k}=0$$
証明の一例
式 \(({\rm A})\) に \(x=-1\) を代入することで $$\sum_{k=0}^n(-1)^k{}_{n}{\rm C}_{k}=(1-1)^n=0$$ を得る。
\({}_{n}{\rm C}_{2k}\)
$$\sum_{k=0}^{\left[\frac{n}{2}\right]} {}_{n}{\rm C}_{2k}=2^{n-1}$$
証明の一例
上記の公式2.1と2.2より
\begin{align}
\sum_{k=0}^n{}_{n}{\rm C}_{k}&=2^n,&
\sum_{k=0}^n(-1)^k{}_{n}{\rm C}_{k}&=0
\end{align}
が成り立つ。これらの各辺の平均をとることで、左辺は \(k\) が奇数の項は打ち消し合い
\begin{align}
\sum_{k=0}^{\left[\frac{n}{2}\right]}{}_{n}{\rm C}_{2k}=\frac{2^n+0}{2}=2^{n-1}
\end{align}
を得る。
\({}_{n}{\rm C}_{2k+1}\)
$$\sum_{k=0}^{\left[\frac{n-1}{2}\right]}{}_{n}{\rm C}_{2k+1}=2^{n-1}$$
証明の一例
上記の公式2.1と2.2より
\begin{align}
\sum_{k=0}^n{}_{n}{\rm C}_{k}&=2^n,&
\sum_{k=0}^n(-1)^k{}_{n}{\rm C}_{k}&=0
\end{align}
が成り立つ。これらの各辺の差をとり \(2\) で割ることで、左辺は \(k\) が偶数の項は打ち消し合い
\begin{align}
\sum_{k=0}^{\left[\frac{n-1}{2}\right]}{}_{n}{\rm C}_{2k+1}=\frac{2^n-0}{2}=2^{n-1}
\end{align}
を得る。
\((-1)^k{}_{n}{\rm C}_{2k}\)
$$\sum_{k=0}^{\left[\frac{n}{2}\right]} (-1)^k{}_{n}{\rm C}_{2k}=2^{\frac{n}{2}}\cos\frac{n\pi}{4}$$
証明の一例
式 \(({\rm A})\) に \(x=\pm i\) を代入することで
\begin{gather}
\sum_{k=0}^n i^k{}_{n}{\rm C}_{k}=(1+i)^n,\\
\sum_{k=0}^n (-i)^k{}_{n}{\rm C}_{k}=(1-i)^n
\end{gather}
が成り立つ。これらの各辺の平均をとることで、左辺は \(k\) が奇数の項は打ち消し合い
\begin{align}
\sum_{k=0}^{\left[\frac{n}{2}\right]}i^{2k}{}_{n}{\rm C}_{2k}=\frac{(1+i)^n+(1-i)^n}{2}
\end{align}
となる。これより
\begin{align}
&\sum_{k=0}^{\left[\frac{n}{2}\right]}(-1)^k{}_{n}{\rm C}_{2k}\\
&\quad=(1+i)^n の実部\\
&\quad=2^{\frac{n}{2}}\left(\cos\frac{n\pi}{4}+i\sin\frac{n\pi}{4}\right)の実部\\[5pt]
&\quad=2^{\frac{n}{2}}\cos\frac{n\pi}{4}
\end{align}
を得る。
※ \(n=0\) のときも成り立つ。
実部の計算で、数学IIIで学ぶ「ド・モアブルの定理」を用いました。
\((-1)^k{}_{n}{\rm C}_{2k+1}\)
$$\sum_{k=0}^{\left[\frac{n-1}{2}\right]}(-1)^k{}_{n}{\rm C}_{2k+1}=2^{\frac{n}{2}}\sin\frac{n\pi}{4}$$
証明の一例
式 \(({\rm A})\) に \(x=\pm i\) を代入することで
\begin{gather}
\sum_{k=0}^n i^k{}_{n}{\rm C}_{k}=(1+i)^n,\\
\sum_{k=0}^n (-i)^k{}_{n}{\rm C}_{k}=(1-i)^n
\end{gather}
が成り立つ。これらの各辺の差をとり \(2\) で割ることで、左辺は \(k\) が偶数の項は打ち消し合い
\begin{align}
\sum_{k=0}^{\left[\frac{n-1}{2}\right]}i^{2k+1}{}_{n}{\rm C}_{2k+1}=\frac{(1+i)^n-(1-i)^n}{2}
\end{align}
となる。これより
\begin{align}
&\sum_{k=0}^{\left[\frac{n-1}{2}\right]}(-1)^k{}_{n}{\rm C}_{2k+1}\\
&\quad=(1+i)^n の虚部\\
&\quad=2^{\frac{n}{2}}\left(\cos\frac{n\pi}{4}+i\sin\frac{n\pi}{4}\right)の虚部\\[5pt]
&\quad=2^{\frac{n}{2}}\sin\frac{n\pi}{4}
\end{align}
を得る。
虚部の計算で、数学IIIで学ぶ「ド・モアブルの定理」を用いました。
\({}_{n}{\rm C}_{3k}\)
$$\sum_{k=0}^{\left[\frac{n}{3}\right]} {}_{n}{\rm C}_{3k}=\frac{1}{3}\left(2^n+2\cos\frac{n\pi}{3}\right)$$
証明の一例
\(1\) の立方根で虚数であるもののひとつを \(\omega\) とおく。このとき、\(1\) の立方根は \(1,\omega,\omega^2\) である。これらを式 \(({\rm A})\) に代入することで
\begin{gather}
\sum_{k=0}^n 1^k{}_{n}{\rm C}_{k}=2^n,\\
\sum_{k=0}^n \omega^k{}_{n}{\rm C}_{k}=(1+\omega)^n,\\
\sum_{k=0}^n (\omega^2)^k{}_{n}{\rm C}_{k}=(1+\omega^2)^n
\end{gather}
が成り立つ。ここで、
\begin{align}
1^k+\omega^k+(\omega^2)^k
=\begin{cases}
3&(k\ が\ 3\ の倍数)\\
0&(その他)
\end{cases}
\end{align}
である。よって、上の \(3\) 式の平均をとることで、
\begin{align}
\sum_{k=0}^{\left[\frac{n}{3}\right]}{}_{n}{\rm C}_{3k}=\frac{2^n+(1+\omega)^n+(1+\omega^2)^n}{3}
\end{align}
となる。
今、\(\displaystyle 1+\omega=\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\) より
\begin{align}
(1+\omega)^n+(1+\omega^2)^n
&=2\times(1+\omega)^nの実部\\[5pt]
&=2\cos\frac{n\pi}{3}
\end{align}
であるので
\begin{align}
\sum_{k=0}^{\left[\frac{n}{3}\right]}{}_{n}{\rm C}_{3k}=\frac{1}{3}\left(2^n+2\cos\frac{n\pi}{3}\right)
\end{align}
を得る。
※ \(n=0\) のときも成り立つ。
\({}_{n}{\rm C}_{4k}\)
$$\sum_{k=0}^{\left[\frac{n}{4}\right]} {}_{n}{\rm C}_{4k}=\frac{1}{2}\left(2^{n-1}+2^{\frac{n}{2}}\cos\frac{n\pi}{4}\right)$$
証明の一例
上記の公式2.3と2.5より
\begin{gather}
\sum_{k=0}^{\left[\frac{n}{2}\right]}{}_{n}{\rm C}_{2k}=2^{n-1},\\
\sum_{k=0}^{\left[\frac{n}{2}\right]}(-1)^k{}_{n}{\rm C}_{2k}=2^{\frac{n}{2}}\cos\frac{n\pi}{4}
\end{gather}
が成り立つ。これらの平均をとることで、左辺は \(k\) が奇数の項は打ち消し合い
\begin{align}
\sum_{k=0}^{\left[\frac{n}{4}\right]}{}_{n}{\rm C}_{4k}
&=\frac{1}{2}\left(2^{n-1}+2^{\frac{n}{2}}\cos\frac{n\pi}{4}\right)
\end{align}
を得る。
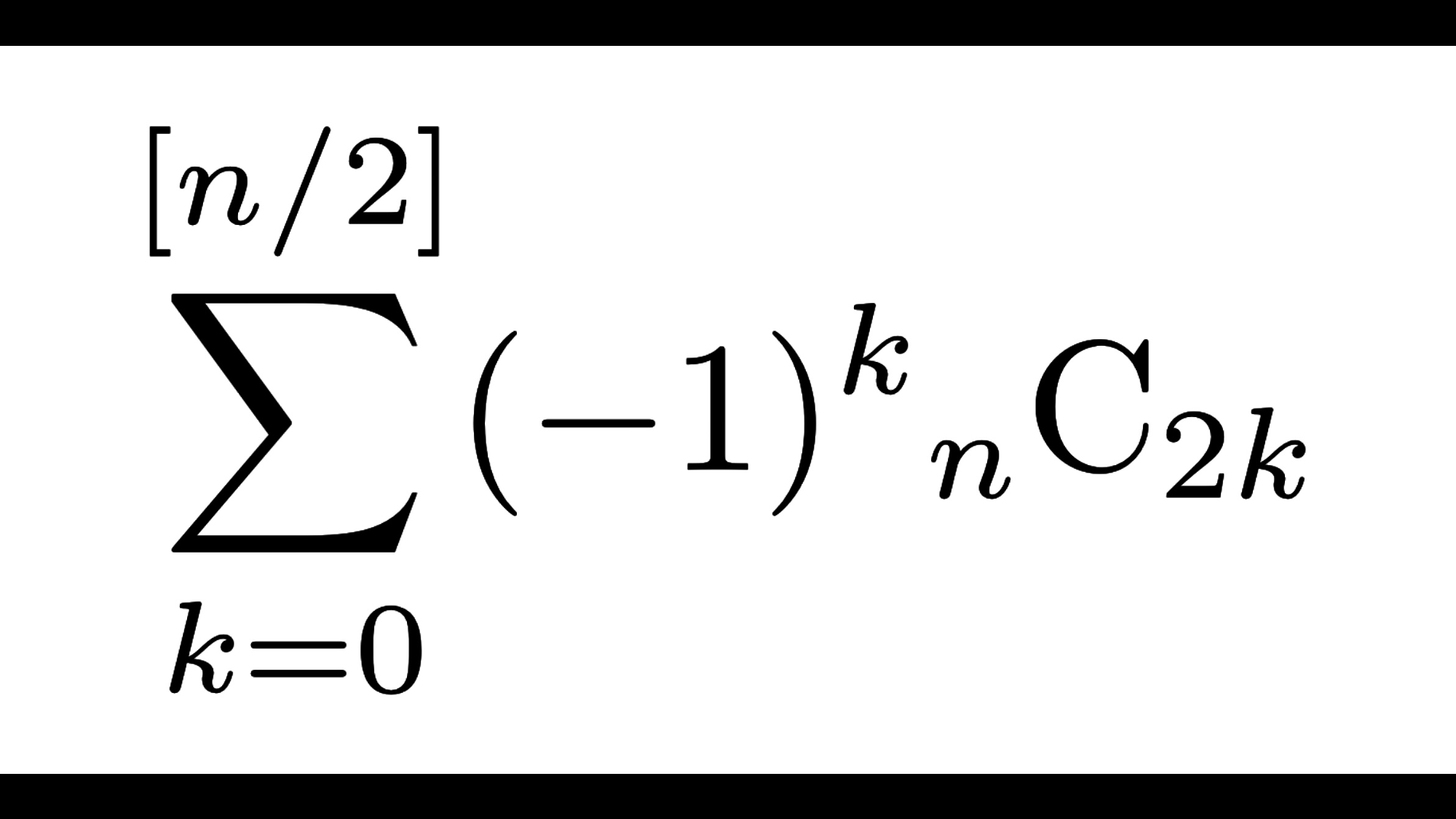
コメント