数学IIで習う 二項係数 \({}_{n}{\rm C}_{k}\) の和を求めます。今回は、数学IIIで学ぶ高次の項の導関数
\begin{align}
\frac{d}{dx}x^k&=kx^{k-1}&&(k=0,1,2,\cdots)
\end{align}
を用います。これにより、以下の「多項式の微分」を扱ってゆきたいと思います。
他の公式は以下の リンク を参照してください。
微分法を用いた和の計算

\(k{}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^n k{}_{n}{\rm C}_{k}=n2^{n-1}$$
証明の一例(その1)
\(n\geq1\) のとき
\begin{align}
\sum_{k=0}^n k{}_{n}{\rm C}_{k}
&=\sum_{k=1}^n k{}_{n}{\rm C}_{k}\\
&=\sum_{k=1}^n n{}_{n-1}{\rm C}_{k-1}\\
&=n(1+1)^{n-1}\\
&=n2^{n-1}
\end{align}を得る。これは \(n=0\) のときも成り立つ。
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k=(1+x)^n
\end{align}が成り立つ。この両辺を微分すると
\begin{align}
\sum_{k=0}^n k {}_{n}{\rm C}_{k}x^{k-1}=n(1+x)^{n-1}
\end{align}となる。これに \(x=1\) を代入することで
\begin{align}
\sum_{k=0}^n k{}_{n}{\rm C}_{k}=n(1+1)^{n-1}=n2^{n-1}
\end{align}を得る。
\(n\geq2\) のとき、代わりに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n (-1)^kk{}_{n}{\rm C}_{k}=0
\end{align}
も成り立ちます。
\(k(k-1){}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^n k(k-1){}_{n}{\rm C}_{k}=n(n-1)2^{n-2}$$
証明の一例(その1)
\(n\geq2\) のとき
\begin{align}
\sum_{k=0}^n k(k-1){}_{n}{\rm C}_{k}
&=\sum_{k=2}^n k(k-1){}_{n}{\rm C}_{k}\\
&=\sum_{k=2}^n n(n-1){}_{n-2}{\rm C}_{k-2}\\
&=n(n-1)(1+1)^{n-2}\\
&=n(n-1)2^{n-2}
\end{align}を得る。これは \(n=0,1\) のときも成り立つ。
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k=(1+x)^n
\end{align}が成り立つ。この両辺を \(2\) 回微分すると
\begin{align}
\sum_{k=0}^n k(k-1){}_{n}{\rm C}_{k}x^{k-2}=n(n-1)(1+x)^{n-2}
\end{align}となる。これに \(x=1\) を代入することで
\begin{align}
\sum_{k=0}^n k(k-1){}_{n}{\rm C}_{k}=n(n-1)2^{n-2}
\end{align}を得る。
\(n\geq3\) のとき、代わりに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n (-1)^kk(k-1){}_{n}{\rm C}_{k}=0
\end{align}
も成り立ちます。
\(k^2{}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^{n} k^2{}_{n}{\rm C}_{k}=n(n+1)2^{n-2}$$
証明の一例(その1)
公式3.1と3.2より
\begin{align}
\sum_{k=0}^n k^2{}_{n}{\rm C}_{k}
&=\sum_{k=0}^n \{k(k-1)+k\}{}_{n}{\rm C}_{k}\\
&=n(n-1)2^{n-2}+n2^{n-1}\\
&=n(n+1)2^{n-2}
\end{align}を得る。
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k=(1+x)^n
\end{align}が成り立つ。この両辺に \(\displaystyle x\frac{d}{dx}\) を \(2\) 回作用させると
\begin{align}
\ \sum_{k=0}^nk^2{}_{n}{\rm C}_{k}x^k
=nx(1+x)^{n-1}+n(n-1)x^2(1+x)^{n-2}
\end{align}となる。これに \(x=1\) を代入することで
\begin{align}
\sum_{k=0}^n k^2{}_{n}{\rm C}_{k}
&=n2^{n-1}+n(n-1)2^{n-2}\\
&=n(n+1)2^{n-2}
\end{align}を得る。
\(n\geq3\) のとき、代わりに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n (-1)^kk^2{}_{n}{\rm C}_{k}=0
\end{align}
も成り立ちます。
\(k(k-1)(k-2){}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^{n} k(k-1)(k-2){}_{n}{\rm C}_{k}=n(n-1)(n-2)2^{n-3}$$
証明の一例(その1)
\(n\geq3\) のとき
\begin{align}
&\sum_{k=0}^n k(k-1)(k-2){}_{n}{\rm C}_{k}\\
&\quad=\sum_{k=3}^n k(k-1)(k-2){}_{n}{\rm C}_{k}\\
&\quad=\sum_{k=3}^n n(n-1)(n-2){}_{n-3}{\rm C}_{k-3}\\
&\quad=n(n-1)(n-2)(1+1)^{n-3}\\
&\quad=n(n-1)(n-2)2^{n-3}
\end{align}を得る。これは \(n=0,1,2\) のときも成り立つ。
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k=(1+x)^n
\end{align}が成り立つ。この両辺を \(3\) 回微分すると
\begin{align}
\ \sum_{k=0}^n k(k-1)(k-2){}_{n}{\rm C}_{k}x^{k-3}=n(n-1)(n-2)(1+x)^{n-3}
\end{align}となる。これに \(x=1\) を代入することで
\begin{align}
\ \sum_{k=0}^n k(k-1)(k-2){}_{n}{\rm C}_{k}=n(n-1)(n-2)2^{n-3}
\end{align}を得る。
\(n\geq4\) のとき、代わりに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n (-1)^kk(k-1)(k-2){}_{n}{\rm C}_{k}=0
\end{align}
も成り立ちます。
\(k^3{}_{n}{\rm C}_{k}\)
$$\sum_{k=0}^{n} k^3{}_{n}{\rm C}_{k}=n^2(n+3)2^{n-3}$$
証明の一例(その1)
公式3.1、3.2、3.4より
\begin{align}
&\sum_{k=0}^n k^3{}_{n}{\rm C}_{k}\\
&\quad=\sum_{k=0}^n \{k(k-1)(k-2)+3k(k-1)+k\}{}_{n}{\rm C}_{k}\\
&\quad=n(n-1)(n-2)2^{n-3}+3n(n-1)2^{n-2}+n2^{n-1}\\[3pt]
&\quad=n^2(n+3)2^{n-3}
\end{align}を得る。
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k=(1+x)^n
\end{align}が成り立つ。この両辺に \(\displaystyle x\frac{d}{dx}\) を \(3\) 回作用させると
\begin{align}
\ \ \sum_{k=0}^nk^3{}_{n}{\rm C}_{k}x^k
=n^3x^3(1+x)^{n-3}+3n^2x^2(1+x)^{n-3}-nx^2(1+x)^{n-3}+nx(1+x)^{n-3}
\end{align}となる。これに \(x=1\) を代入することで
\begin{align}
\sum_{k=0}^nk^3{}_{n}{\rm C}_{k}
&=n^32^{n-3}+3n^22^{n-3}-n2^{n-3}+n2^{n-3}\\
&=n^2(n+3)2^{n-3}
\end{align}を得る。
\(n\geq4\) のとき、代わりに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n (-1)^kk^3{}_{n}{\rm C}_{k}=0
\end{align}
も成り立ちます。
\((-1)^kk^n{}_{n}{\rm C}_{k}\)
$$\sum_{k=1}^n (-1)^kk^n{}_{n}{\rm C}_{k}=(-1)^nn!$$
証明の一例
関数 \(f(x)=(1+x)^n\) に対して、多項式 \(g(x)\) で
\begin{align}
\left(x\frac{d}{dx}\right)^nf(x)=n!x^n+(1+x)g(x)
\end{align}なるものが存在する。ここで、$$f(x)=\sum_{k=0}^n {}_{n}{\rm C}_{k}x^k$$ でもあるので
\begin{align}
\left(x\frac{d}{dx}\right)^nf(x)=\sum_{k=0}^n k^n{}_{n}{\rm C}_{k}x^k
\end{align}である。これらに \(x=-1\) を代入すと
\begin{align}
\sum_{k=0}^n (-1)^kk^n{}_{n}{\rm C}_{k}
&=\left(x\frac{d}{dx}\right)^nf(-1)\\
&=n!\times(-1)^n+(1-1)g(-1)\\
&=(-1)^nn!
\end{align}を得る。
\(f(x)\) に \(\displaystyle x\frac{d}{dx}\) を \(n\) 回だけ作用させれば、\(x=-1\) を代入しても \(0\) にはなりませんでしたね!
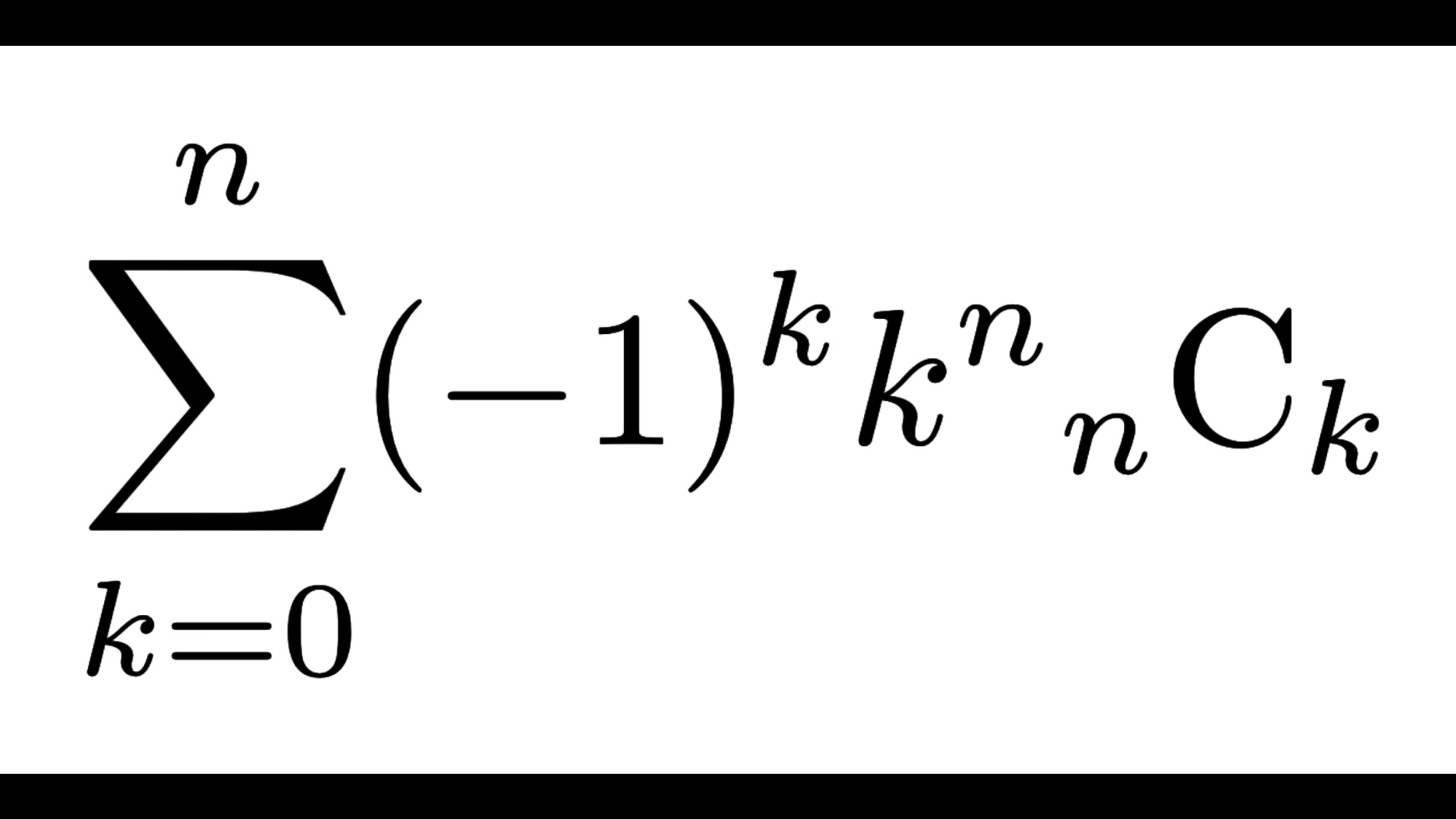
コメント