数学IIで習う 二項係数 \({}_{n}{\rm C}_{k}\) の和を求めます。今回は、指数法則を用いて
\begin{align}
(1+x)^{l+m}=(1+x)^l(1+x)^m
\end{align}
などとして、各辺の特定の次数の係数を比較してみます。これにより、以下の「係数比較の方法」を扱ってゆきたいと思います。
他の公式は以下の リンク を参照してください。
係数比較を用いた和の計算

\(({}_{l}{\rm C}_{k})({}_{m}{\rm C}_{n-k})\)
$$\sum_{k=0}^n \left({}_{l}{\rm C}_{k}\right)\left({}_{m}{\rm C}_{n-k}\right)={}_{l+m}{\rm C}_{n}$$
証明の一例
\(x\) の多項式に関して、指数法則より
\begin{align}
(1+x)^l(1+x)^m=(1+x)^{l+m}
\end{align}が成り立つ。\(l\) 及び \(m\) 以下の非負整数 \(n\) に対して、両辺の \(x^n\) の係数を比較することで
\begin{align}
\sum_{k=0}^n \left({}_{l}{\rm C}_{k}\right)\left({}_{m}{\rm C}_{n-k}\right)={}_{l+m}{\rm C}_{n}
\end{align}を得る。
これを「ヴァンデルモンドの畳み込み」という。
\(\left({}_{n}{\rm C}_{k}\right)^2\)
$$\sum_{k=0}^n \left({}_{n}{\rm C}_{k}\right)^2={}_{2n}{\rm C}_{n}$$
証明の一例
\(x\) の多項式に関して、指数法則より
\begin{align}
(1+x)^n(1+x)^n=(1+x)^{2n}
\end{align}が成り立つ。両辺の \(x^n\) の係数を比較することで
\begin{align}
\sum_{k=0}^n \left({}_{n}{\rm C}_{k}\right)\left({}_{n}{\rm C}_{n-k}\right)={}_{2n}{\rm C}_{n}
\end{align}すなわち、\({}_{n}{\rm C}_{n-k}={}_{n}{\rm C}_{k}\) より
\begin{align}
\sum_{k=0}^n \left({}_{n}{\rm C}_{k}\right)^2={}_{2n}{\rm C}_{n}
\end{align}を得る。
\(k\left({}_{n}{\rm C}_{k}\right)^2\)
$$\sum_{k=0}^n k\left({}_{n}{\rm C}_{k}\right)^2=\frac{n}{2}{}_{2n}{\rm C}_{n}$$
証明の一例
\(x\) の多項式に関して、指数法則、及び、二項定理より
\begin{align}
(1+x)^{2n}
&=(1+x)^n(1+x)^n\\
&=\left(\sum_{k=0}^n{}_{n}{\rm C}_{k}x^k\right)\left(\sum_{k=0}^n{}_{n}{\rm C}_{k}x^k\right)
\end{align}が成り立つ。両辺を \(x\) で微分すると
\begin{align}
2n(1+x)^{2n-1}
=2\left(\sum_{k=0}^n{}_{n}{\rm C}_{k}x^k\right)\left(\sum_{k=0}^nk{}_{n}{\rm C}_{k}x^{k-1}\right)
\end{align}となる。\(n\geq1\) に対して、両辺の \(x^{n-1}\) の係数を比較することで
\begin{align}
2n{}_{2n-1}{\rm C}_{n-1}=2\sum_{k=0}^n \left({}_{n}{\rm C}_{k}\right)\left(k{}_{n}{\rm C}_{n-k}\right)
\end{align}すなわち、\({}_{n}{\rm C}_{n-k}={}_{n}{\rm C}_{k}\) より
\begin{align}
\sum_{k=0}^n k\left({}_{n}{\rm C}_{k}\right)^2
&=n{}_{2n-1}{\rm C}_{n-1}\\
&=\frac{n}{2}{}_{2n}{\rm C}_{n}
\end{align}を得る。これは \(n=0\) のときも成り立つ。
\({}_{m+k}{\rm C}_{m}\)
$$\sum_{k=0}^{n} {}_{m+k}{\rm C}_{k}={}_{m+n+1}{\rm C}_{n}$$
証明の一例
\(x\) の多項式に関して
\begin{align}
1+(1+x)+\cdots+(1+x)^{m+n}
&=\frac{(1+x)^{m+n+1}-1}{(1+x)-1}\\
&=\frac{(1+x)^{m+n+1}-1}{x}
\end{align}が成り立つ。このとき、左辺の \(x^m\) の係数は
\begin{align}
{}_{m}{\rm C}_{m}+{}_{m+1}{\rm C}_{m}+\cdots+{}_{m+n}{\rm C}_{m}
&=\sum_{k=0}^{n} {}_{m+k}{\rm C}_{m}
\end{align}となり、右辺の分子の \(x^{m+1}\) の係数は
\begin{align}
{}_{m+n+1}{\rm C}_{m+1}
&={}_{m+n+1}{\rm C}_{n}
\end{align}となる。よって、
\begin{align}
\sum_{k=0}^{n} {}_{m+k}{\rm C}_{m}
&={}_{m+n+1}{\rm C}_{n}
\end{align}を得る。
\({}_{n+k}{\rm C}_{n}\)
$$\sum_{k=0}^{n} {}_{n+k}{\rm C}_{k}={}_{2n+1}{\rm C}_{n}$$
証明の一例
\(x\) の多項式に関して
\begin{align}
1+(1+x)+\cdots+(1+x)^{2n}
&=\frac{(1+x)^{2n+1}-1}{(1+x)-1}\\
&=\frac{(1+x)^{2n+1}-1}{x}
\end{align}が成り立つ。このとき、左辺の \(x^n\) の係数は
\begin{align}
{}_{n}{\rm C}_{n}+{}_{n+1}{\rm C}_{n}+\cdots+{}_{2n}{\rm C}_{n}
&=\sum_{k=0}^{n} {}_{n+k}{\rm C}_{n}
\end{align}となり、右辺の分子の \(x^{n+1}\) の係数は
\begin{align}
{}_{2n+1}{\rm C}_{n+1}
&={}_{2n+1}{\rm C}_{n}
\end{align}となる。よって、
\begin{align}
\sum_{k=0}^{n} {}_{n+k}{\rm C}_{n}
&={}_{2n+1}{\rm C}_{n}
\end{align}を得る。
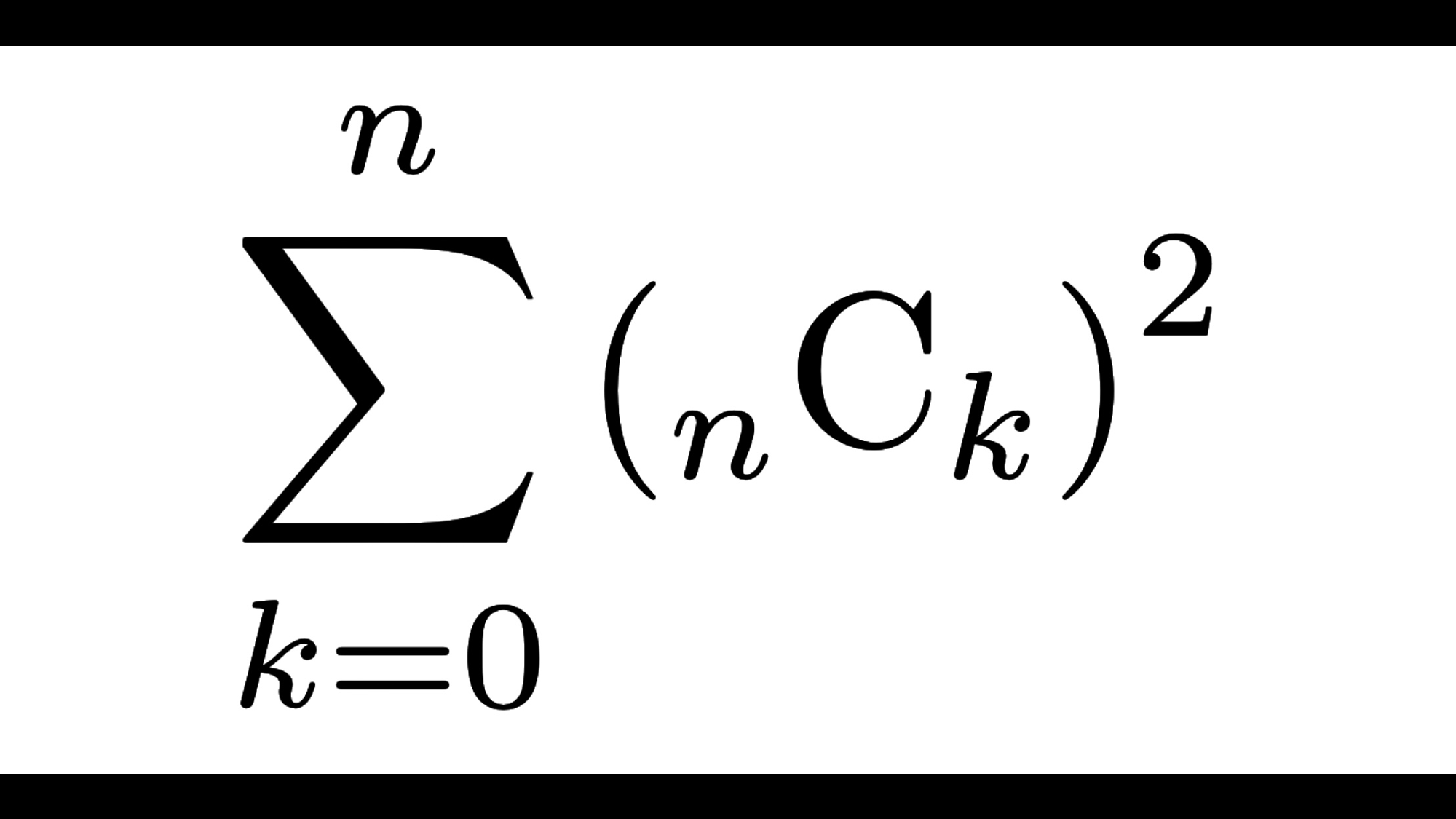
コメント