数学IIで習う 二項係数 \({}_{n}{\rm C}_{k}\) の和を求めます。今回は、少し難しいものも含めて扱います。
他の公式は以下の リンク を参照してください。
その他の難しい和の計算

\({}_{n-k}{\rm C}_{k}\)
$$\sum_{k=0}^{\left[n/2\right]} {}_{n-k}{\rm C}_{k}=F_{n+1}$$
証明の一例
まず、二項係数 \({}_{n}{\rm C}_{k}\) について、整数 \(k\) が \(k<0\) または \(k>n\) となるとき
\begin{align}
{}_{n}{\rm C}_{k}&=0
\end{align}と定義して拡張する。このとき、任意の整数 \(k\) に対して
\begin{align}
{}_{n}{\rm C}_{k}+{}_{n}{\rm C}_{k+1}={}_{n+1}{\rm C}_{k+1}
\end{align}が成り立つ。
次に、数列 \(\{a_n\}\) を $$a_n=\sum_{k=0}^{\left[n/2\right]} {}_{n-k}{\rm C}_{k}$$ と定めると、二項係数の拡張から $$a_n=\sum_{k=0}^{n} {}_{n-k}{\rm C}_{k}$$ と書ける。これより、
\begin{align}
a_n+a_{n+1}
&=\sum_{k=0}^{n} {}_{n-k}{\rm C}_{k}+\sum_{k=0}^{n+1} {}_{n+1-k}{\rm C}_{k}\\
&=\sum_{k=1}^{n+1} {}_{n+1-k}{\rm C}_{k-1}+\sum_{k=0}^{n+1} {}_{n+1-k}{\rm C}_{k}\\
&=\sum_{k=0}^{n+1} {}_{n+1-k}{\rm C}_{k-1}+\sum_{k=0}^{n+1} {}_{n+1-k}{\rm C}_{k}\\
&=\sum_{k=0}^{n+1} \left({}_{n+1-k}{\rm C}_{k-1}+{}_{n+1-k}{\rm C}_{k}\right)\\
&=\sum_{k=0}^{n+1} {}_{n+2-k}{\rm C}_{k}\\
&=\sum_{k=0}^{n+2} {}_{n+2-k}{\rm C}_{k}\\
&=a_{n+2}
\end{align}が成り立つ。
さて、
\begin{align}
a_0&=\sum_{k=0}^{0} {}_{-k}{\rm C}_{k}={}_{0}{\rm C}_{0}=1\\
a_1&=\sum_{k=0}^{0} {}_{1-k}{\rm C}_{k}={}_{1}{\rm C}_{0}=1
\end{align}であるので、フィボナッチ数列の第 \(n\) 項を \(F_n\) とおくと $$\sum_{k=0}^{\left[n/2\right]} {}_{n-k}{\rm C}_{k}=a_n=F_{n+1}$$ が成り立つ。
例えば、数列 \(\{b_n\}\) を $$b_n=\sum_{k=0}^{\left[n/3\right]} {}_{n-2k}{\rm C}_{k}$$ と定義します。このとき、\(b_1=1\),\(b_2=1\),\(b_3=2\) であって、漸化式 $$b_{n+3}=b_{n+2}+b_n$$ を満たします。
\((-1)^k\left({}_{2n}{\rm C}_{k}\right)^3\)
$$\sum_{k=0}^{2n} (-1)^k\left({}_{2n}{\rm C}_{k}\right)^3=(-1)^n\frac{(3n)!}{(n!)^3}$$
証明の一例
(以下の証明は こちらのサイト を参考にしました。標準的な高校数学の内容を超えています。)
二項係数の拡張
二項係数の定義 $${}_{n}{\rm C}_{k}=\frac{n(n-1)\cdots(n-k+1)}{k!}$$ より、\(x\) に関する \(k\) 次多項式 $${}_{x}{\rm C}_{k}=\frac{x(x-1)\cdots(x-k+1)}{k!}$$ を考える。
示したいこと
\(2n\) 次多項式 \(P(x)\) を $$P(x)=(-1)^n({}_{x}{\rm C}_{n})({}_{x+n}{\rm C}_{n})$$ で定義する。また、同じく\(2n\) 次の多項式 \(Q(x)\) を $$Q(x)=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{x}{\rm C}_{k})({}_{x}{\rm C}_{2n-k})$$ で定義する。
各々の \(x=2n\) のときの値を計算すると
\begin{align}
P(2n)
&=(-1)^n({}_{2n}{\rm C}_{n})({}_{3n}{\rm C}_{n})\\
&=(-1)^n\times\frac{(2n)!}{n!n!}\times\frac{(3n)!}{n!(2n)!}\\
&=(-1)^n\frac{(3n)!}{(n!)^3}
\end{align}及び
\begin{align}
Q(2n)
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{2n}{\rm C}_{k})({}_{2n}{\rm C}_{2n-k})\\
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{2n}{\rm C}_{k})({}_{2n}{\rm C}_{k})\\
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})^3
\end{align}となる。これらはそれぞれ示したい式の右辺と左辺である。
よって、多項式 \(P(x)\) と \(Q(x)\) が一致することが示れば十分である。具体的には、等式 $$P(x)=Q(x)$$ を満たす相異なる \(x\) が \(2n\) 個より多く存在することを確認する。
\(P(x)=0\) の \(2n\) 個の解
まず、$$P(x)=(-1)^n({}_{x}{\rm C}_{n})({}_{x+n}{\rm C}_{n})$$ において、多項式 \({}_{x}{\rm C}_{n}\) は $$x=0,1,\cdots,n-1$$ を根に持つ。また、多項式 \({}_{x+n}{\rm C}_{n}\) は $$x=-n,-n+1,\cdots,-1$$ を根に持つ。
以上より、方程式 \(P(x)=0\) は相異なる \(2n\) 個の値 $$-n,-n+1,\cdots,n-2,n-1$$ を解に持つ。
\(Q(x)=0\) の \(2n\) 個の解
\(x=0,1,\cdots,n-1\) について
次に、$$Q(x)=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{x}{\rm C}_{k})({}_{x}{\rm C}_{2n-k})$$ において \(x=0,1,\cdots,n-1\) とする。
\(k\leq x\) なる \(k\) に対して \(x<2n-k\) なので \({}_{x}{\rm C}_{2n-k}=0\) となる。
\(k>x\) なる \(k\) に対して \({}_{x}{\rm C}_{k}=0\) となる。
以上より、方程式 \(Q(x)=0\) は相異なる \(n\) 個の値 $$0,1,\cdots,n-1$$ を解に持つ。
\(x=-n,-n+1,\cdots,-1\) について
また、\(x=-y-1\) とおくと
\begin{align}
Q(x)
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{x}{\rm C}_{k})({}_{x}{\rm C}_{2n-k})\\
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{-y-1}{\rm C}_{k})({}_{-y-1}{\rm C}_{2n-k})\\
&=\sum_{k=0}^{2n}(-1)^k{}_{2n}{\rm C}_{k}\times(-1)^k{}_{y+k}{\rm C}_{k}\times(-1)^{2n-k}{}_{y+2n-k}{\rm C}_{2n-k}\\
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{y+k}{\rm C}_{k})({}_{y+2n-k}{\rm C}_{2n-k})
\end{align}となる。
ここで、\(y=0,1,\cdots,n-1\) とする。このとき
\begin{align}
Q(x)
&=\sum_{k=0}^{2n}(-1)^k({}_{2n}{\rm C}_{k})({}_{y+k}{\rm C}_{y})({}_{y+2n-k}{\rm C}_{y})
\end{align}となる。
今、\(({}_{y+k}{\rm C}_{y})({}_{y+2n-k}{\rm C}_{y})\) は \(k\) の \(2y\) 次多項式であって、\(y\) は \(0\) 以上 \(n\) 未満である。よって、\(k\) には依らない定数 \(a_i\) を用いて
\begin{align}
({}_{y+k}{\rm C}_{y})({}_{y+2n-k}{\rm C}_{y})=\sum_{i=0}^{2n-2}a_ik^i
\end{align}と書ける。これより
\begin{align}
Q(x)
&=\sum_{k=0}^{2n}(-1)^k{}_{2n}{\rm C}_{k}\left(\sum_{i=0}^{2n-2}a_ik^i\right)\\
&=\sum_{i=0}^{2n-2}a_i\left\{\sum_{k=0}^{2n}(-1)^k{}_{2n}{\rm C}_{k}k^i\right\}\\
&=\sum_{i=0}^{2n-2}(a_i\times0)\\
&=0
\end{align}が成り立つ。
以上より、方程式 \(Q(x)=0\) は相異なる \(n\) 個の値 $$-n,-n+1,\cdots,-1$$ を解に持つ。
\(P(x)=Q(x)\) となる \(x\) の存在
ここまで、\(2n\) 個の値 $$x=-n,-n+1,\cdots,n-2,n-1$$ において $$P(x)=Q(x)=0$$ となることを見た。
今、\(x=n\) とする。
\(0\leq k<n\) なる \(k\) に対して \(n<2n-k\) なので \({}_{n}{\rm C}_{2n-k}=0\) となる。
\(n<k\leq 2n\) なる \(k\) に対して \({}_{n}{\rm C}_{k}=0\) となる。
よって、\(Q(x)\) の和は \(k=n\) のときのみ計算すれば良く
\begin{align}
Q(n)
&=(-1)^n({}_{2n}{\rm C}_{n})({}_{n}{\rm C}_{n})({}_{n}{\rm C}_{2n-n})\\
&=(-1)^n({}_{2n}{\rm C}_{n})\\
&=P(n)
\end{align}が成り立つ。
結論
\(P(x)\) と \(Q(x)\) は \(2n\) 次の多項式であって、相異なる \(2n+1\) 個の値 $$x=-n,-n+1,\cdots,n-1,n$$ において \(P(x)=Q(x)\) が成り立つ。よって、等式 \(P(x)=Q(x)\) は恒等式となる。
ここで、\(x=2n\) とすることで $$P(2n)=Q(2n)$$ すなわち $$\sum_{k=0}^{2n} (-1)^k\left({}_{2n}{\rm C}_{k}\right)^3=(-1)^n\frac{(3n)!}{(n!)^3}$$ を得る。
お疲れ様でした。
この等式は、少し変形して $$\sum_{k=-n}^{n} (-1)^k\left({}_{2n}{\rm C}_{n+k}\right)^3=\frac{(3n)!}{(n!)^3}$$ と書かれ、ディクソンの恒等式 と呼ばれます。
これの一般化が以下の公式6.3です。こちらも同様の方法で証明することができますが、超幾何級数と呼ばれるものを用いた証明も知られています。(例えば、こちらのサイト において「超幾何級数I」の系3.5, 系3.6 を参照してください。)
\((-1)^{k}\left({}_{a+b}{\rm C}_{a+k}\right)\left({}_{b+c}{\rm C}_{b+k}\right)\left({}_{c+a}{\rm C}_{c+k}\right)\)
$$\sum_{k=-\infty}^{\infty} (-1)^{k}\left({}_{a+b}{\rm C}_{a+k}\right)\left({}_{b+c}{\rm C}_{b+k}\right)\left({}_{c+a}{\rm C}_{c+k}\right)=\frac{(a+b+c)!}{a!b!c!}$$
上記の通り、この公式は紹介のみに留めます。
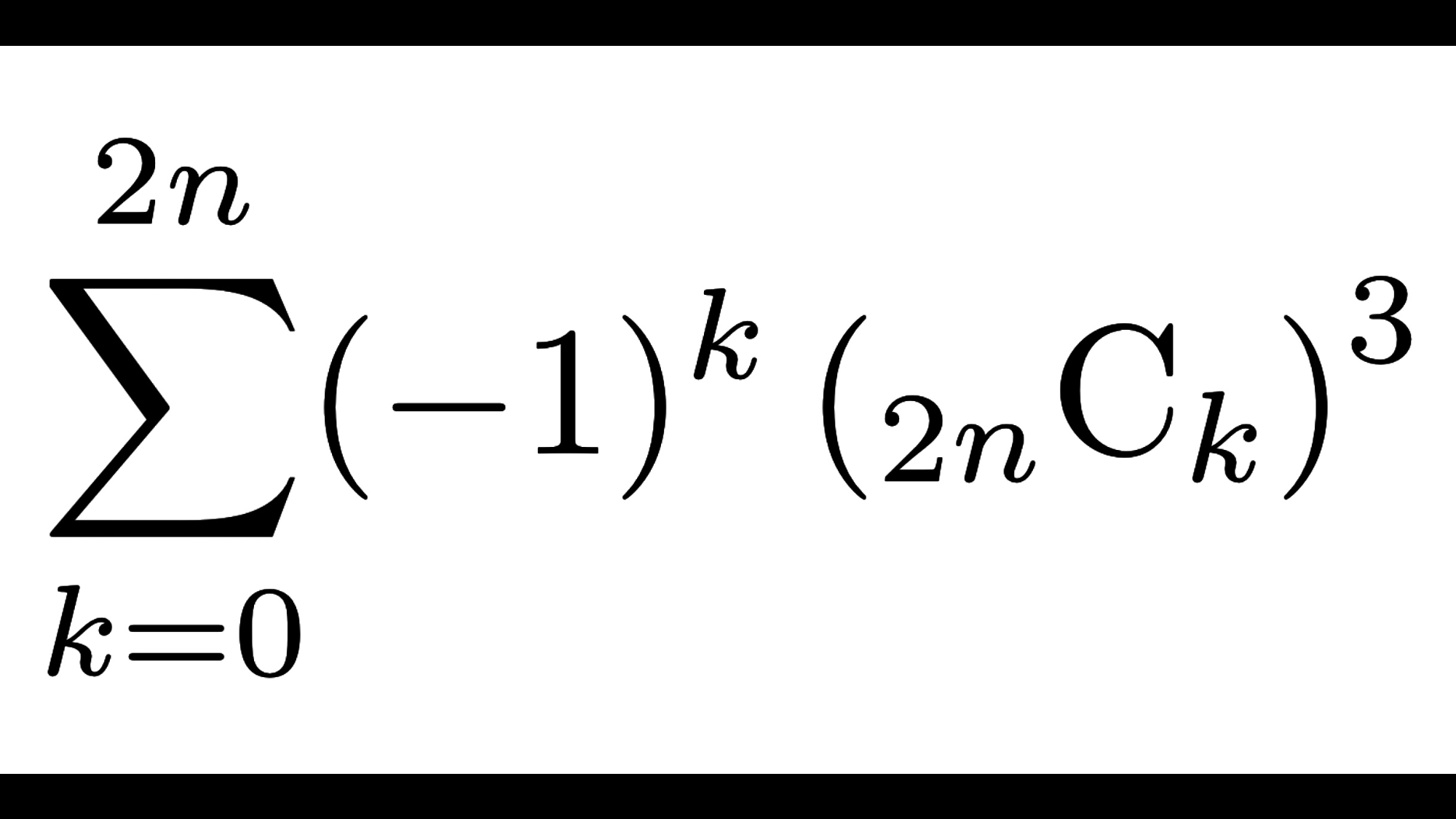
コメント