「円周率 π は 3.05 よりも、3.14 よりも大きい！」ウォリスの公式で東大入試を解く。

本日は3月14日「円周率の日」ということで、今回のテーマは円周率 $\pi$ と $3.14$ の関係です。

円周率は $3.05$ より大きいでしょうか。答えは、大きいです。円周率 $\pi$ は、多くの人が小学生の頃に $3.14$ で代用して計算してきたと思います。そのことからも納得できるでしょう。

関連して、2003年に東京大学の入試で次の問題が出題されました。

東大入試

円周率が $3.05$ より大きいことを証明せよ。

ただ、大学入試ですから「円周率 $\pi$ はだいたい $3.14$ だから…」と解答することはできませんね。

そもそも、過去の記事でも証明したように、$\pi$ を小数で表記すると小数点以下が周期なく無限に続くことがわかっています。とくに、ピッタリ $3.14$ ではないということです。そこで、次の問題を考えます。

問題

円周率 $\pi$ は $3.14$ より大きいか。

答えは「$3.14$ より大きい」です。

これら二つの問題に対して、一般的に知られたものとは少し異なる説明を与えたいと思います。

まずは、東大入試のよく知られた解法に触れたのち、“ウォリスの公式” を用いて解きます。次に、その公式の説明を行います。そして最後に、円周率 $\pi$ が $3.14$ より大きいことの説明を行います。

東大入試の自然な解き方。
実際に東大入試に挑戦しよう！
1. ウォリスの公式を分析する
2. 実際に Excel で確認する
気になる方へ：公式を導出します。
最後に。

東大入試の自然な解き方。

ここでは、円周率の定義に基づいた、自然な方針を紹介します。

そもそも円周率 $\pi$ は次のように定義されます。

円の直径を $R$、円周の長さを $L$ とするとき、比率 $\displaystyle \frac{L}{R}$ を円周率と呼び、$\pi$ と表す。

この定義に基づくと、自然な解法としては次のものが考えられます。

直径 $R$ の円の内部に多角形を描いて $$(多角形の周の長さ)<L=\pi R$$ のように下から評価する。

この入試について少し検索してみると、適当な半径の円を設定し、その内部にうまく多角形を描く方法がいくつかみつかります。確かに、それらは自然な発想による解き方だと思います。

しかし！

私は、このような「円周率が〇〇より大きいことを示せ。」という問題を、多角形を用いた方法以外で解きたいのです。そこで使いたいのが “ウォリスの公式” と呼ばれる公式です。公式の導出は後に回すとして、実際に公式を活用してみましょう！

実際に東大入試に挑戦しよう！

いよいよ、東大入試を解いてゆきます。

ウォリスの公式を分析する

まず、偶数の平方 $(2n)^2$ を用いて分数を作ります。それを $n=1,2,\cdots$ と順にかけ合わせることで、極限値として円周率が出現するというのが ウォリスの公式 です。

ウォリスの公式

\begin{align}
\frac{\pi}{2}
&=\prod_{n=1}^\infty \frac{(2n)^2}{(2n)^2-1}\\
&=\frac{4}{3}\times\frac{16}{15}\times\frac{36}{35}\times\frac{64}{63}\times\frac{100}{99}\times\cdots
\end{align}

さて、ウォリスの公式の途中までの部分積を $a_n$ とおきます。

$$a_n=\prod_{k=1}^n \frac{(2k)^2}{(2k)^2-1}$$

このとき、

$$\frac{a_n}{a_{n-1}}=\frac{(2n)^2}{(2n)^2-1}>1$$

となるので、数列 $\{a_n\}$ は単調に増加することがわかります。

また、この数列を用いると、ウォリスの公式は

\begin{align}
\frac{\pi}{2}
&=\prod_{n=1}^\infty \frac{(2n)^2}{(2n)^2-1}\\
&=\lim_{n\to\infty} \prod_{k=1}^n \frac{(2k)^2}{(2k)^2-1}\\
&=\lim_{n\to\infty} a_n
\end{align}

と書くことができます。

数列 $\{a_n\}$ は単調に増加し、$\dfrac{\pi}{2}$ に収束する。

これによって何がわかるのか。

$a_1=\dfrac{4}{3}=1.333\cdots>1.33$ なので $\dfrac{\pi}{2}>a_1>1.33$ である。よって、両辺を $2$ 倍することで $$\pi>2\times1.33=2.66$$ を得る。
$a_2=\dfrac{4}{3}\times\dfrac{16}{15}=1.422\cdots>1.42$ なので $\dfrac{\pi}{2}>a_2>1.42$ である。よって、両辺を $2$ 倍することで $$\pi>2\times1.42=2.84$$ を得る。
$a_3=\dfrac{4}{3}\times\dfrac{16}{15}\times\dfrac{36}{35}=1.462\cdots>1.46$ なので $\dfrac{\pi}{2}>a_3>1.46$ である。よって、両辺を $2$ 倍することで $$\pi>2\times1.46=2.92$$ を得る。

このように、円周率 $\pi$ の下からの評価が可能になります！

しかも、数列 $\{a_n\}$ が $\dfrac{\pi}{2}$ に収束することから、$n$ を大きくすればいくらでも精度を上げることができます。

実際に Excel で確認する

どのような $n$ を見つけたいか

さて、この東大入試で示したいことは $\pi>3.05$ ですね。

上の議論より、常に $\dfrac{\pi}{2}>a_n$ です。この両辺を $2$ 倍することで $\pi>2a_n$ を得ます。これを用いて $\pi>3.05$ を示ればよいので、

$$2a_n \geq 3.05$$

となるような $n$ を見つけましょう。

実際に見つけるための手順

入試本番では不可能ですが、ここでは Excel を使ってみます。数列 $\{a_n\}$ の漸化式を考えると

$$a_n=a_{n-1}\times\frac{(2n)^2}{(2n)^2-1}$$

です。$a_1=\dfrac{4}{3}$ なので、空白のシートを開いて…

A1セルに $1$ を、B1セルに $=4/3$ を、C1セルに $={\rm B1}*2$ を入力する。
A2セルに $2$ を、B2セルに $={\rm B1}*(2*{\rm A2})^2/((2*{\rm A2})^2-1)$ を、C2セルに $={\rm B2}*2$ を入力する。
3つのセル A2:C2 を選択し、第10行まで連続データを生成する。

このように入力すると以下のようになります。（A列が $n$ の値、B列が $a_n$ の値、C列が $2a_n$ の値を表しています。）

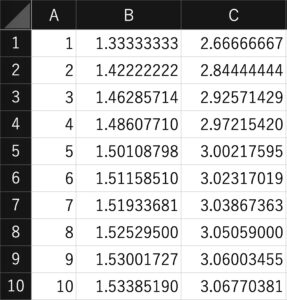
つまり、C8セルより

\begin{align}
2a_8
&=2\times\frac{4}{3}\times\frac{16}{15}\times\frac{36}{35}\times\frac{64}{63}\times\frac{100}{99}\times\frac{144}{143}\times\frac{196}{195}\times\frac{256}{255}\\[3pt]
&=2\times\frac{106542032486400}{69850115960625}\\[3pt]
&=3.0505\cdots\\
&>3.05
\end{align}

を計算できたので、$\pi>2a_8>3.05$ を得ました。これで、東大入試が解けたことになります！

冒頭の問題

問題

円周率 $\pi$ は $3.14$ より大きい。

での結果が知りたい方は、このページを少し飛ばしてスクロールし、本文の最後まで進んでください。

気になる方へ：公式を導出します。

Step.1 ウォリス積分を定義する

$n=0,1,2,\cdots$ に対して定まる次の定積分 $I_n$ をウォリス積分と呼びます。（$\sin^0 \theta=1$ と解釈するものとします。）

$$I_n=\int_0^{\frac{\pi}{2}}\sin^n\theta d\theta$$

数列 $\{I_n\}$ について、次の性質がわかります。

数列 $\{I_n\}$ は単調に減少する。また、$I_0=\dfrac{\pi}{2}$，$I_1=1$ である。

解説

$\displaystyle 0\leq\theta\leq\frac{\pi}{2}$ において $\sin \theta$ が $0$ から $1$ の間の値をとることから、数列 $\{I_n\}$ は単調に減少することがわかります。また、$$I_0=\int_0^{\frac{\pi}{2}} d\theta=\left[\theta\right]_0^{\frac{\pi}{2}}=\frac{\pi}{2}$$ さらに、$$I_1=\int_0^{\frac{\pi}{2}}\sin\theta d\theta=\left[-\cos\theta\right]_0^{\frac{\pi}{2}}=1$$ であることもわかります。

Step.2 漸化式からわかること

数列 $\{I_n\}$ の性質に加えて、その漸化式を考えると次が成り立ちます。これが、上で紹介したウォリスの公式の左辺を与えます。

$$\lim_{n\to\infty}n{I_n}^2=\frac{\pi}{2}\tag{1}$$

解説

まず、$n\geq2$ とします。$I_n$ に対して部分積分を施すことで、次の漸化式を得ます。$$nI_n=(n-1)I_{n-2}$$ 両辺に $I_{n-1}$ をかけると数列 $\{nI_{n-1}I_n\}$ が定数列であることがわかるので、以下の等式を得ます。$$nI_{n-1}I_n=1\times I_0\times I_1=\frac{\pi}{2}$$ 次に、数列 $\{I_n\}$ が単調減少であったことから $$I_{n+1}<I_n<I_{n-1}$$ ですが、各辺に $nI_n$ をかけることで $$nI_nI_{n+1}<n{I_n}^2<nI_{n-1}I_n$$ すなわち、以下の不等式を得ます。$$\frac{n}{n+1}\times\frac{\pi}{2}<n{I_n}^2<\frac{\pi}{2}$$ 最後に、はさみうちの原理より式(1)を得ます。

Step.3 漸化式を具体的に解く

一方、その漸化式を具体的に解いてみることで、次の表示を得ます。

$$I_{2k+1}=\prod_{l=1}^k \frac{2l}{2l+1}=\frac{2}{3}\times\frac{4}{5}\times\cdots\times\frac{2k}{2k+1}\tag{2}$$

解説

先ほどの漸化式 $nI_n=(n-1)I_{n-2}$ より $$I_n=\frac{n-1}{n}I_{n-2}$$ となるので、例えば $n=2k+1$ ($k$ は整数) のとき $$I_{2k+1}=\frac{2k}{2k+1}I_{2k-1}$$ となります。この関係式を繰り返し用いることで式(2)を得ます。

Step.4 結論を導く

この $I_{2k+1}$ の表示を式(1)の左辺に代入することで、上で紹介したウォリスの公式の右辺の形を得ます。

$$\frac{\pi}{2}=\prod_{l=1}^\infty \frac{(2l)^2}{(2l)^2-1}\tag{4}$$

解説

式(1)より $n{I_n}^2$ の極限がわかっていました。式(2)を用いるために $n=2k+1$ として、$(2k+1){I_{2k+1}}^2$ を計算してみましょう。

\begin{align}
(2k+1){I_{2k+1}}^2
&=(2k+1)\left(\prod_{l=1}^k \frac{2l}{2l+1}\right)^2\\
&=(2k+1)\left(\prod_{l=1}^k \frac{2l}{2l+1}\right)\left(\prod_{l=1}^k \frac{2l}{2l+1}\right)\\
&=\left(\prod_{l=1}^k \frac{2l}{2l-1}\right)\left(\prod_{l=1}^k \frac{2l}{2l+1}\right)\\
&=\prod_{l=1}^k \frac{(2l)^2}{(2l-1)(2l+1)}\\
&=\prod_{l=1}^k \frac{(2l)^2}{(2l)^2-1}
\end{align}

よって、次が成り立ちます。

\begin{align}
\lim_{n\to\infty}n{I_n}^2
&=\lim_{k\to\infty}(2k+1){I_{2k+1}}^2\\
&=\prod_{l=1}^\infty \frac{(2l)^2}{(2l)^2-1}\tag{3}
\end{align}

以上、式(1)と式(3)より、ウォリスの公式(4)を得ます！

補足動画

今回は「ウォリスの公式を使うこと」に焦点を当てているので、ピントをぼかさないためにも公式の導出は流れを述べるに留めた部分もあります。その導出過程の行間を埋めて、成り立ちをガッツリと理解したい方はこちらの関連動画をご覧ください。

ウォリス積分について

スターリングの公式について

最後に。

今回は、ウォリスの公式を用いて $\pi$ を下から評価し、東京大学の入試を解いてみました。これは、一般に「円周率が ◯◯ より大きいことを示せ。」というタイプの問題に（理論上は）使えるわけです。

ここまで読んでくださった方に、冒頭に紹介した問題

問題

円周率 $\pi$ は $3.14$ より大きい。

を解決する様子をお見せして終わりにしましょう。

先ほど作成した Excel の表について、第500行あたりまで連続データを生成します。

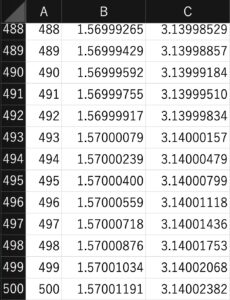
このとき、C493セルより

\begin{align}
2a_{493}
&=2\times\prod_{n=1}^{493} \frac{(2n)^2}{(2n)^2-1}\\[3pt]
&=2\times\frac{17356117569415920976614398052862288106294108918260842489752040900517290597144772146206595724083342717126180129380459133337046428248359112563056799892107531856480998319767058934116579515528456160773805967205802597878089394843631011009061523751690811747884777583418764978300698720557911507964029300045405425040800507944935930490118292290665109019611428929049907228411254309183652523667337664773553334314806994798582607537882209692767993056412731693638420712885215985503448321212404702370178532407768935789600071643043622329873725055541837708880548059350399652974476235686600488890461932222129834308403339080396387266186094470154606180905905301854764507517965424225415330216193964773587313186737823887289216907417766990823299359793285583550485048289102021597528668549623009604279633402294032901434257305650670650270867765929621666857210855462193060093311000373827784839590301896084866581066403341553587160749623272505674368247541820304046705534183474144744038448385260444429455338977756135000403080105027224739273137263976002607200701912027297160165152685011593833442197467182522736401731163445941297167684403957571932707121402788736649702331944248491225946736599418796224728839498138986341162075671337501591245938385153524583096172414270742235687947873187707454800650197075913232703765625470493109394171387302944907053628733564430713439520795198087519810620094830420417940262534860138782374779055457815599815946887416073270747644023961081933361490582725019151365236755565676928526441452118321358840946675257252862196314041407047598683666114611139445915565584964178525992116216762312660628803723972512767709352418622842542406949992436280994973800648787417660549604732947985796421290616738976852624411792699927408908600800388786008469369992233352304352299683483016424780907244410439888684149612527788787884125396193070912954404745579973869271035692072249851559025477880127221829184987333516876417565724109647193474102477898987538460080307201568410669875117192019357606390414040434485308281774038711525867724274178513120382450147664453136706137304189703011305210700743215792520290704818548214457440582723640584282748564415611935014459695240779793592368409422640595376137756762321636831265957838930209885026683656106181720681140722721596721287354197711390656045422393217025636988999182648868864000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000}{11054846423162961493381311310835621927408660553002622868792863729317435377443940430076728146530120536836545836296233866763700447549828093965157293172494782808604845506211312079998596310326656447768541476317532733120960400343605218020002062792436973665740732004917250674892265873472539088192194602648359967922403454721033948512090928858675866135340146094764610317466584351494304046844520725189352482868084290203665769081336807013401994996477935829072717343324638672196504516092330119047626260216360315615331170882049153679139617706575303159193339392597230309009707792890862788214333626778794704156182068123518290981787719077880984324187167774321636160185503517103810979330082706173598131907820018184210215054832608628037824194516051567762228992849905468591984701300609034220227707450211338487554555775859088801942609970365064219379185654959306354648920943676276686015092427007512366385991018446013715355280503411955027566966569962717906994725595028616200956550079601828144451519207036084214839820819834838789658774094306381278491945272799758316369686868751928667978166601341335123412211213226446931519638371576506436353498709369731988465527528130740797992525232453954815293387353324944490749536591757760300464800337792487041974246532670101898444030157022292364425618575814888750471164085067763407485046968314107498567193358056333326518515131196374806665051733676023505420013907123762785746393983551218431078439987480523465478943926647985623208050389294733274934824523371013971695926700958373232566523808022407906950207070849833000702066268733960169292938247209058626809254143735972261863563785642831703400966654543996226484756400967126537493574534893628436982511769738028972015289732732487834038689341835173609329865717073533841713528945075211873901247232386053240360598834835111588605077057713056037305487871855274711492529431256192758242104691292984931802795032642401638698830142505378237783867635437883163065691361630944925203038128559404399736233351601388738313147107407590915822723201218661634823304723980580819860130946822284938673840414750965150359872485080715058365534201104903947025476405826079850378622607934741704039953481891612531382483664686095158432721616125667307850205378119874828286071327903058281406698921116935815374813514515531500081182978624708570652542569224356484063906252605667883413291905027841068820232492057189530317849755260549804083493473404828234502858271779061882093179958821822758321523935242863833337299243509677094686254277082485762561376684037169577999419611824549747325363568961620330810546875}\\[3pt]
&=3.1400015\cdots\\
&>3.14
\end{align}

であるので、$\pi>2a_{493}>3.14$ を得ます。これで、問題が解けたことになります！

お疲れ様でした。