みなさん、“組立除法” は好きですか?
私はそこまで好きではありませんでした。
組立除法は因数分解の問題などで役に立ちますね。通常の多項式の筆算を行わず、計算を行う回数が少ないことがメリットとなるわけです。
「組立除法が好き!」と答えたみなさんの中で、なぜ組立除法で商や余りが求められるのか正しく説明できる方はどれくらいいるでしょうか。原理を理解して使っていますか?
私は高校時代に “なんだか上手く計算できてしまう便利な道具” として組立除法を教わったので、どこか腑に落ちず、納得して使えずにいました。
本記事では、私と同様に「なぜ?」と気になってしまい、その恩恵を受けることができていないみなさんが、私と一緒に少しでも組立除法を受け入れられるようになることを目指します。
※本記事では通常の多項式の筆算による説明は行わず、数式で理解を助けます。
題材となる問題です。

突然ですが、あなたは
多項式 \(x^5+4x^4+4x^3+3x^2+2x+6\) を因数分解せよ。
という問題にはどのようにアプローチしますか?(特に断りがなければ因数分解は係数が有理数の範囲です。)
まず、与式は奇数次の多項式ですから、(与式) \(=0\) とした方程式は少なくともひとつの実数解を持ちます。その実数解の中に有理数解があるであろうという見立てのもと「代入して \(=0\) となる有理数 \(\alpha\) 」を探します。そんな有理数 \(\alpha\) が見つかれば、与式を \((x-\alpha)\) で割ることで次数を着実に減らし、因数分解を進めることができます!
また、この多項式は整数係数ですから、その有理数 \(\alpha\) の候補は定数項 \(6\) の約数である \(\pm 1\),\(\pm 2\),\(\pm 3\),\(\pm 6\) であって、これらを順に代入して値が \(0\) になるか確認してゆくわけですね。ただし、今回は次数の高い \(x^5\) がありますから、代入して計算するのは \(\pm 3\) あたりから嫌な気持ちになりますし、\(\pm 6\) をやる必要性が生じた瞬間に手に持ったペンを机に一度置くことでしょう…。
そこで、組立除法を使える人は与式を \((x+3)\) などで割った商や余りを組立除法によって比較的楽に確認できるわけです。
我々は、それを “与えられたアルゴリズム” としてではなく、“理解し納得したアルゴリズム” として扱えるようになることを目指します。
一旦、組立除法に関する中途半端な知識は捨て去って、まっさらな気持ちで受け入れる体制を整えてから考察を進めましょう!
「余り」に着目し組立除法を構成する!

剰余定理に工夫を施す
まず、与式を
\begin{align}
P(x)=x^5+4x^4+4x^3+3x^2+2x+6
\end{align}とおきます。このとき、\(P(x)\) を \((x-\alpha)\) で割った余りは、剰余定理より
\begin{align}
P(\alpha)=\alpha^5+4\alpha^4+4\alpha^3+3\alpha^2+2\alpha+6\tag{1}
\end{align}となります。
数学的には正しいです。ただ、問題は実際に計算する手間をいかに省くかですよね。
例えば、\(\alpha=6\) を代入する計算をイメージしていただくと、最も重い計算は \(\alpha^5\) です。
- \(\alpha^5\) を計算するときは、\(\alpha\) を \(5\) 個かけ合わせなければなりません。
- 次の項の \(\alpha^4\) を計算するときは \(\alpha\) を \(4\) 個かけ合わせなければなりません。
- さらに次の \(\alpha^3\) を計算するときは…
このように、それなりに重い \(\alpha\) をかけるという計算 \(\times\alpha\) を何度も繰り返すことになってしまいます。式(1)に従って具体的に \(P(\alpha)\) を計算するときには、各係数も考慮すると \(5+4+3+2+1=15\) 回も \(\times\alpha\) をしますね。
そこで、「 \(\times\alpha\) の回数を少なくしたい!」という方針を念頭に置いて \(P(\alpha)\) に式変形を施してみましょう。部分的に \(\alpha\) で括ってゆきます。
\begin{align}
P(\alpha)
&=\alpha^5+4\alpha^4+4\alpha^3+3\alpha^2+2\alpha+6\\
&=(\alpha^4+4\alpha^3+4\alpha^2+3\alpha+2)\alpha+6\\
&=((\alpha^3+4\alpha^2+4\alpha+3)\alpha+2)\alpha+6\\
&=(((\alpha^2+4\alpha+4)\alpha+3)\alpha+2)\alpha+6\\
&=((((\alpha+4)\alpha+4)\alpha+3)\alpha+2)\alpha+6\tag{2}
\end{align}
例えば、式(1)の方が見た目で何をしているかは伝わりやすいかもしれませんが、\(\times\alpha\) は \(15\) 回でした。
一方、次数が大きくなればなるほど式(1)に比べて式(2)の方が計算回数は少なく(今回は \(\times\alpha\) が \(5\) 回で済みましたね!)、計算機などでは処理が少なく済みます。
ホーナー法で余りを計算する
ここでは一般に、多項式
\begin{align}
P(x)=a_0x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5\tag{3}
\end{align}を考えます。
代入したときのかけ算 \(\times x\) の計算回数を少なくするために、式(2)と同様に
\begin{align}
P(x)=((((a_0x+a_1)x+a_2)x+a_3)x+a_4)x+a_5\tag{4}
\end{align}と変形して計算する方法を ホーナー法(Horner’s method)といいます。
今回の場合、かけ算 \(\times x\) の計算回数は
- 式(3)では \(5+4+3+2+1=15\) 回
- 式(4)では \(1+1+1+1+1=5\) 回
のように減っていますね!(一般に次数 \(n\) の多項式の場合は \(n(n+1)/2\) 回から \(n\) 回に減ります。)
具体的に、 \((x+1)\) で割ったときの余り \(P(-1)\) の計算を、式(4)を見つめながら順を追って見てゆきましょう。
Step0.スタートは最高次の係数 \(a_0\) とする。
Step1.それに \(-1\) をかけて \(a_1\) を加える。
Step2.それに \(-1\) をかけて \(a_2\) を加える。
Step3.それに \(-1\) をかけて \(a_3\) を加える。
Step4.それに \(-1\) をかけて \(a_4\) を加える。
Step5.それに \(-1\) をかけて \(a_5\) を加える。
いかがでしょうか。係数の情報さえ記憶しておけば同様の操作を繰り返すだけですよね。ホーナー法は、ただ計算回数を減らすだけでなく、そのアルゴリズムも単純化(反復化)されるのです。
この同様に手順を繰り返すイメージ、すぐに再登場するので覚えておいてください!
このような \(P(\alpha)\) の計算は \(\alpha\) と各係数 \(a_0\),\(a_1\),\(a_2\),\(a_3\),\(a_4\),\(a_5\) のみで構成されていたので、それらを用いた可能な限りシンプルな記述方法を考え、代入計算に活かしたいと思います。
組立除法の記法を考案する
一般的な話から戻ってきて、改めて
多項式 \(P(x)=x^5+4x^4+4x^3+3x^2+2x+6\) を因数分解せよ。
について考えましょう。
\(P(\alpha)=0\) なる有理数 \(\alpha\) の候補は \(\pm 1\),\(\pm 2\),\(\pm 3\),\(\pm 6\) でしたが、与式 \(P(x)\) の係数は全て正なので、正の解 \(1\),\(2\),\(3\),\(6\) はあり得ないですね。
そこで、\(\alpha=-1\) となるかどうかをホーナー法の考えに従って丁寧に見てゆきましょう。
\(\alpha=-1\) となるか?
まず、係数と \(\alpha\) の候補の \(-1\) を並べて書き、係数の下に一行分のスペースを空けて線を引きます。
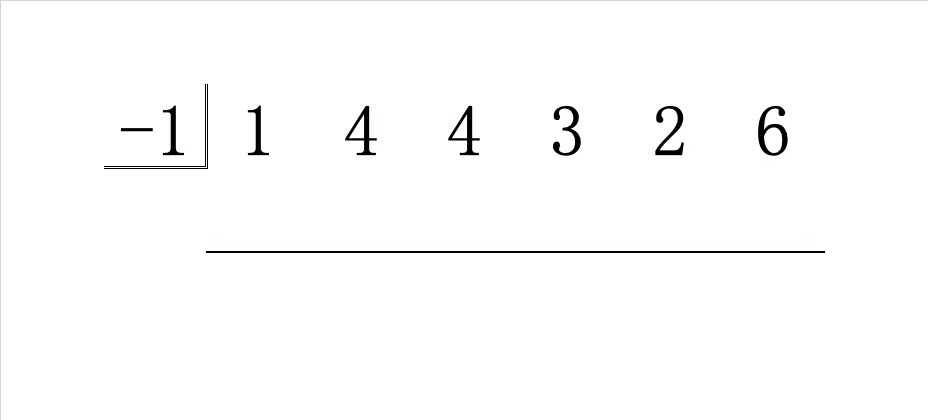
各係数には後に足し算を行うので、足す数 ◯ を書くスペースを空けておくのです。その下に、各々の和を書くことになります。
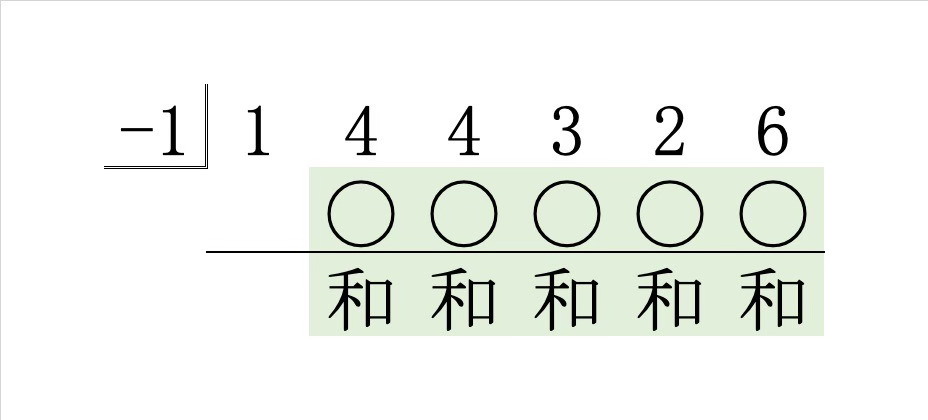
※ 左上にある “\(-1\)” を書く位置は好みで変えて構いません。
Step0.最高次の係数 \(1\) をそのまま下に書き写します。
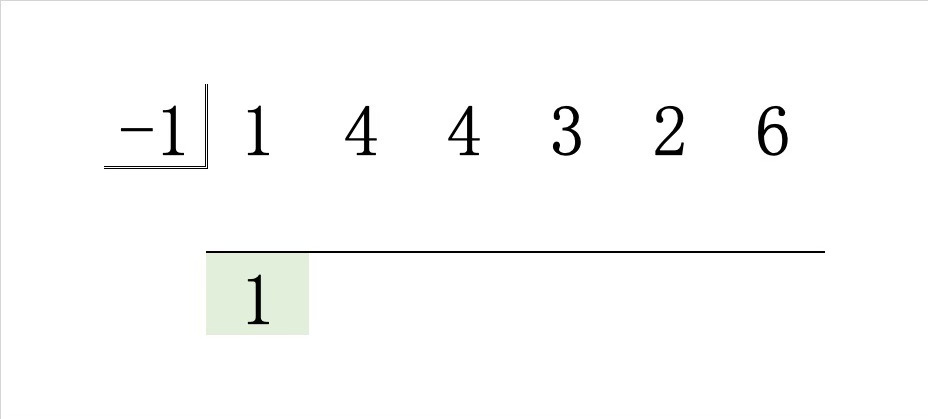
Step1.その係数 \(1\) に \(-1\) をかけた積を右斜め上に書き、縦の和を線の下に書きます。
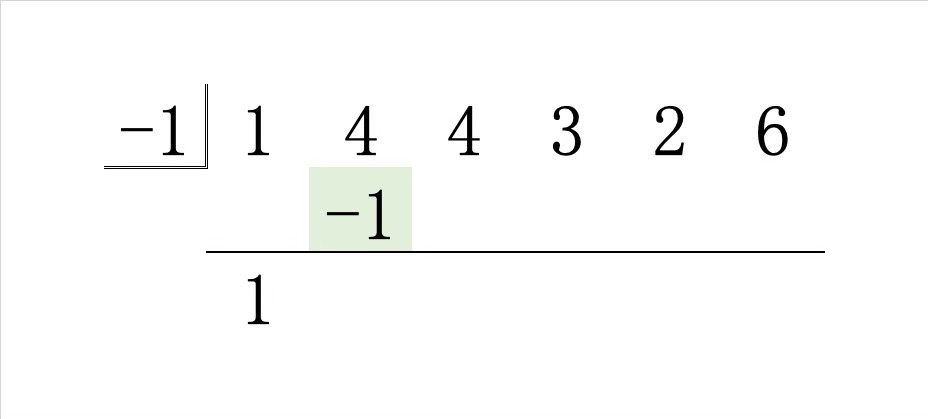
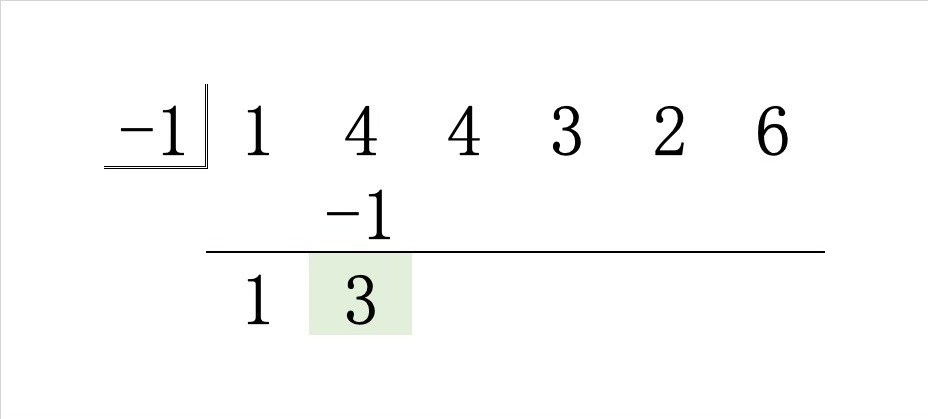
Step2.その和 \(3\) に \(-1\) をかけた積を右斜め上に書き、縦の和を線の下に書きます。
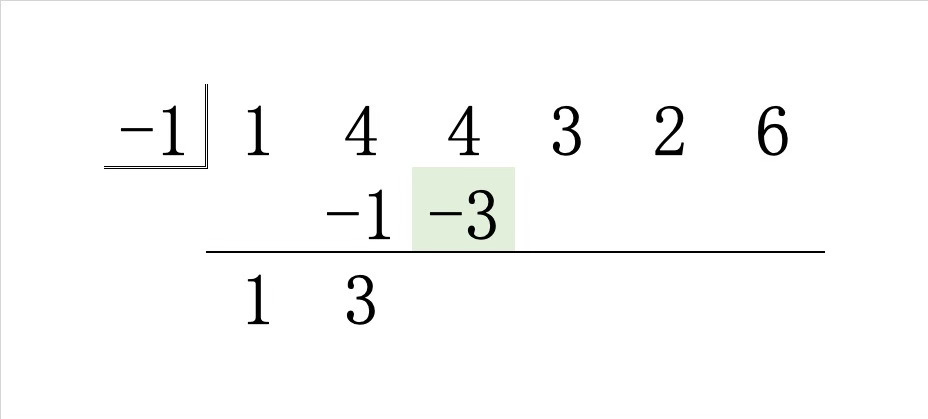
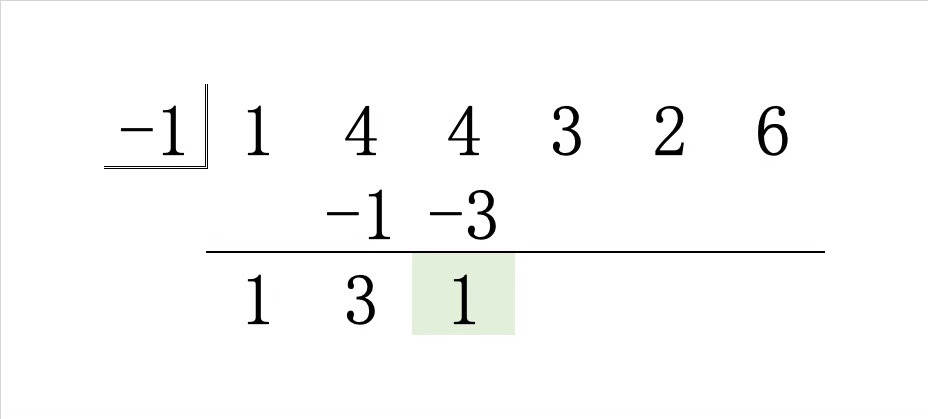
Step3.その和 \(1\) に \(-1\) をかけた積を右斜め上に書き、縦の和を線の下に書きます。
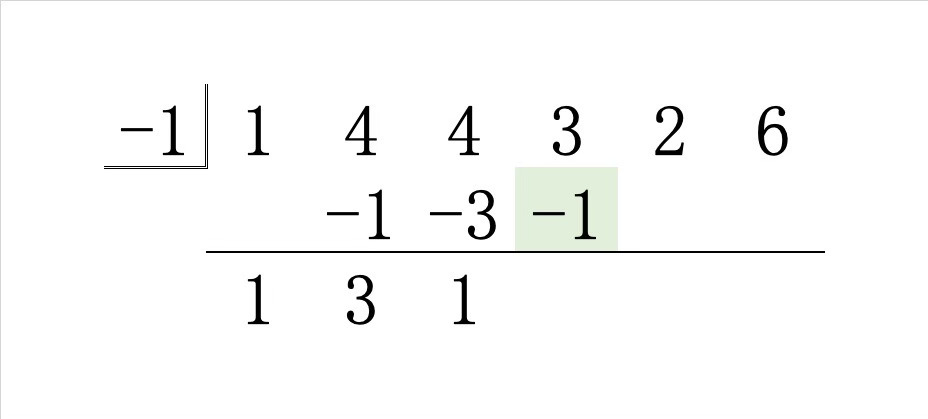
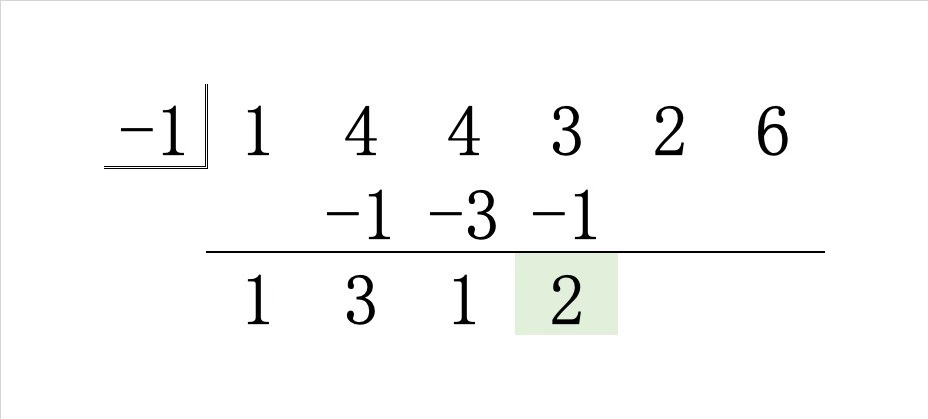
Step4.その和 \(2\) に \(-1\) をかけた積を右斜め上に書き、縦の和を線の下に書きます。
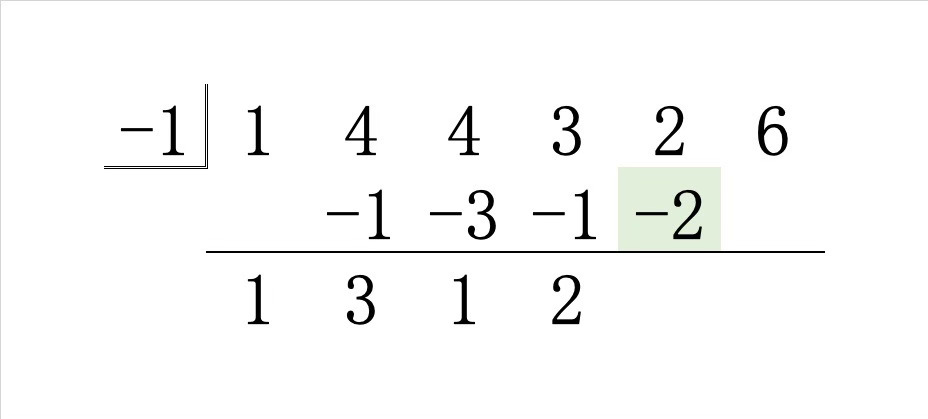
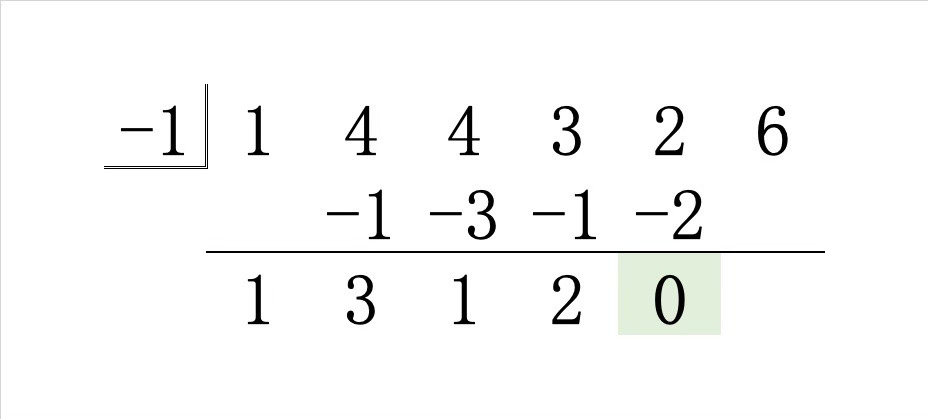
Step5.その和 \(0\) に \(-1\) をかけた積を右斜め上に書き、縦の和を線の下に書きます。
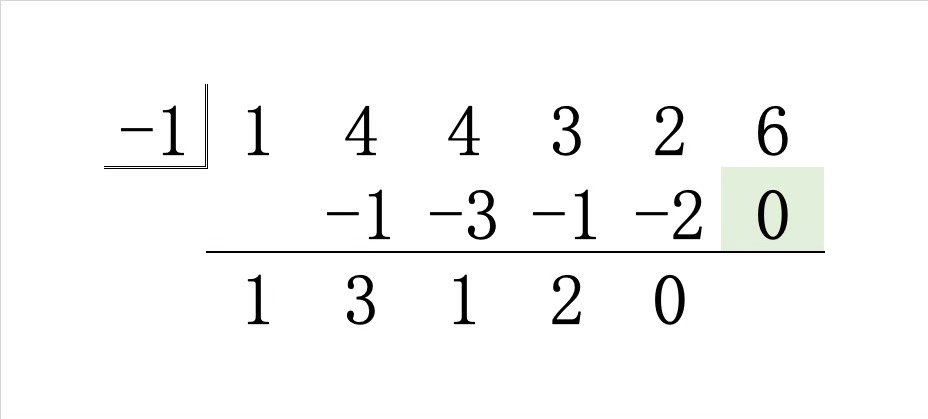
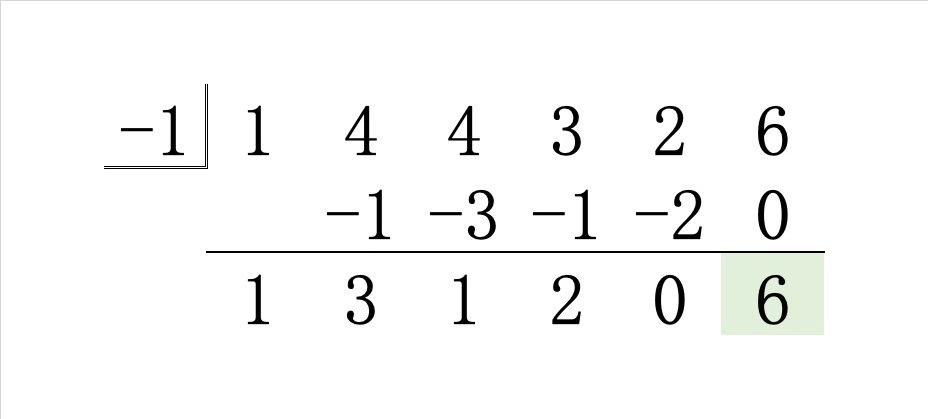
右端まで到達したら、最後に線の下に書いた数が求めたかった代入した値 \(P(-1)\) です。
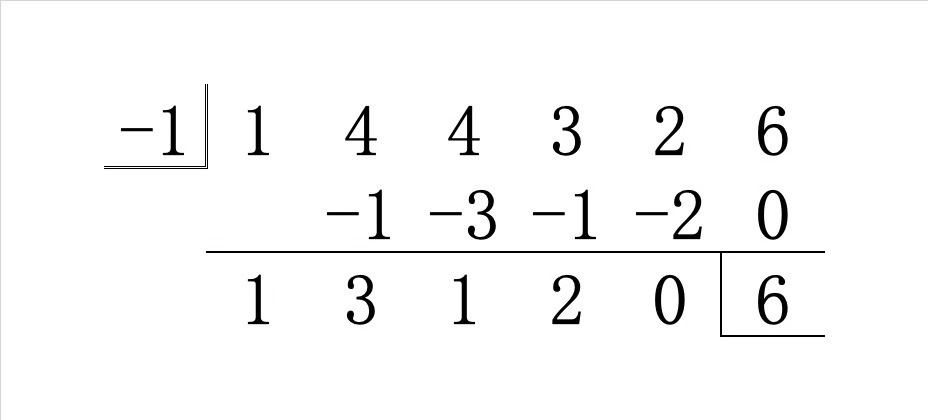
今回は \(P(-1)=6\) であって \(0\) ではないので、因数定理より与式 \(P(x)\) は \((x+1)\) では割り切れないということですね。
以上の計算を、その記述方法から「組立除法」と呼びます。
\(\alpha=-2\) となるか?
次に \(\alpha\) の候補として \(-2\) を採用した場合、同様に組立除法を行うと以下のようになります。
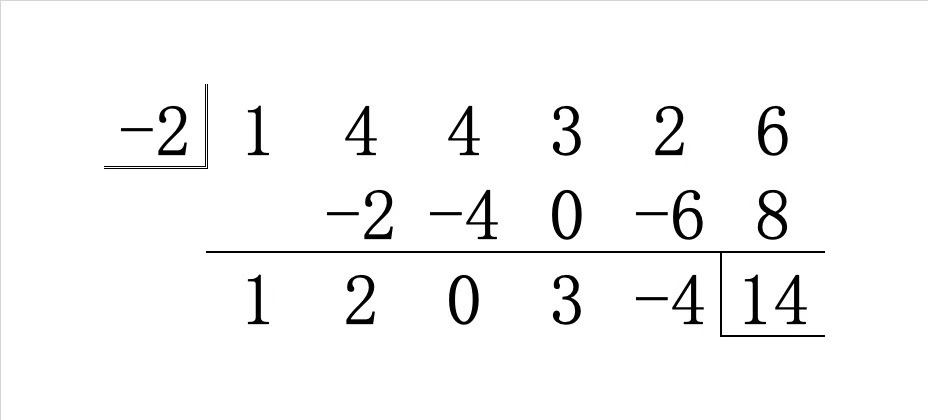
これより \(P(-2)=14\neq0\) であるので、因数定理より与式 \(P(x)\) は \((x+2)\) でも割り切れないということがわかります。
\(\alpha=-3\) となるか?
続いて \(\alpha\) の候補として \(-3\) を採用した場合は以下のようになります。
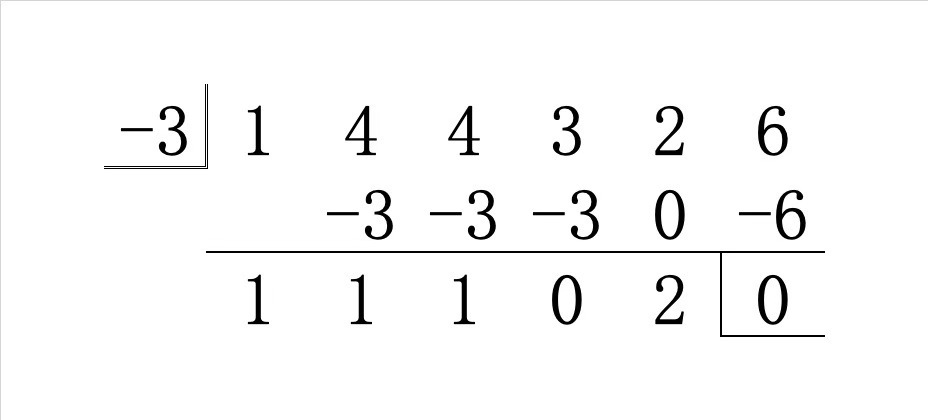
これより \(P(-3)=0\) であるので、因数定理より与式 \(P(x)\) は \((x+3)\) で割り切れる!というわけです。
組立除法では「商」も求められている!

組立除法で得たものの正体
ここまでは、多項式 \(P(x)\) を \((x-\alpha)\) で割ったときの「余り」 \(R=P(\alpha)\) をホーナー法に即した組立除法によって計算してきました。
では、組立除法で「商」を求めることはできないでしょうか?
…できます。できています。
今まで計算してきた \(P(x)=x^5+4x^4+4x^3+3x^2+2x+6\) を用いて説明してゆきます。
\(\alpha=-1\) のとき
組立除法の結果は以下の通りでした。
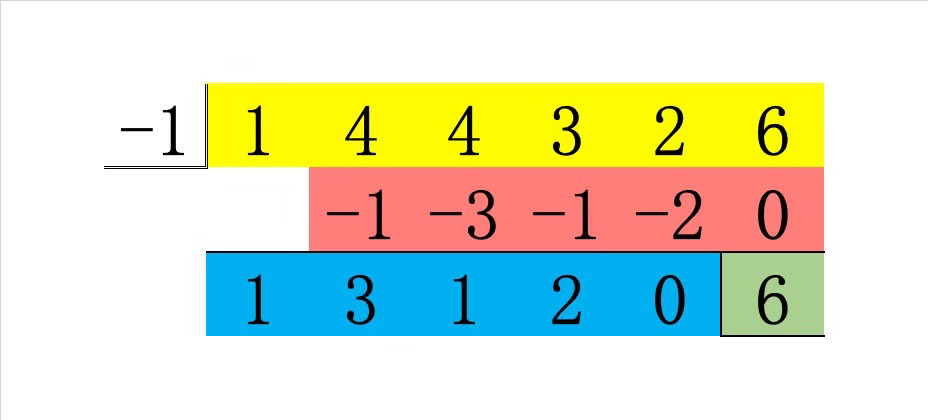
青の部分に相当する多項式 $$1\cdot x^4+3\cdot x^3+1\cdot x^2+2\cdot x+0$$ すなわち $$x^4+3x^3+x^2+2x$$ を \(Q(x)\) とおきます。
このとき、赤の部分に相当する式は \(-Q(x)\) となることがわかります。
黄色の部分が元の多項式 \(P(x)\) ですから、組立除法で行った足し算より
P(x)+(-Q(x))=Q(x)x+6
となります。(余りの 6 を緑マーカーで塗る方法がわかりませんでした…)すなわち、赤の部分を移項することにより
\begin{align}
P(x)=Q(x)(x+1)+6
\end{align}を得ます。
つまり、知りたかった「商」は青の部分の $$Q(x)=x^4+3x^3+x^2+2x$$ だということがわかりました!
\(\alpha=-2\) のとき
組立除法の結果は以下の通りでした。
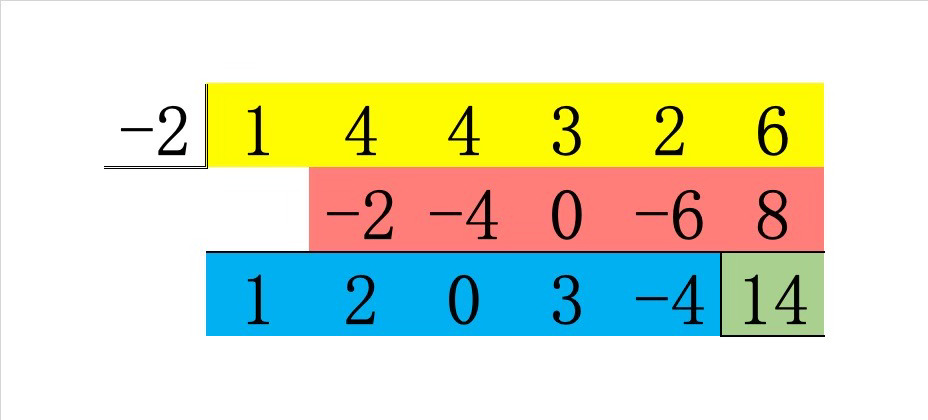
青の部分に相当する多項式 $$x^4+2x^3+3x-4$$ を \(Q(x)\) とおくと、赤の部分は \(-2Q(x)\) となりますね。
黄色の部分が元の多項式 \(P(x)\) ですから、同様に組立除法より
P(x)+(-2Q(x))=Q(x)x+14
となります。(この余りの 14 は緑マーカーで…)すなわち、赤の部分を移項することにより
\begin{align}
P(x)=Q(x)(x+2)+14
\end{align}を得ます。
やはり、知りたかった商は青の部分の $$Q(x)=x^4+2x^3+3x-4$$ でした!
\(\alpha=-3\) のとき
組立除法の結果は以下の通りでした。
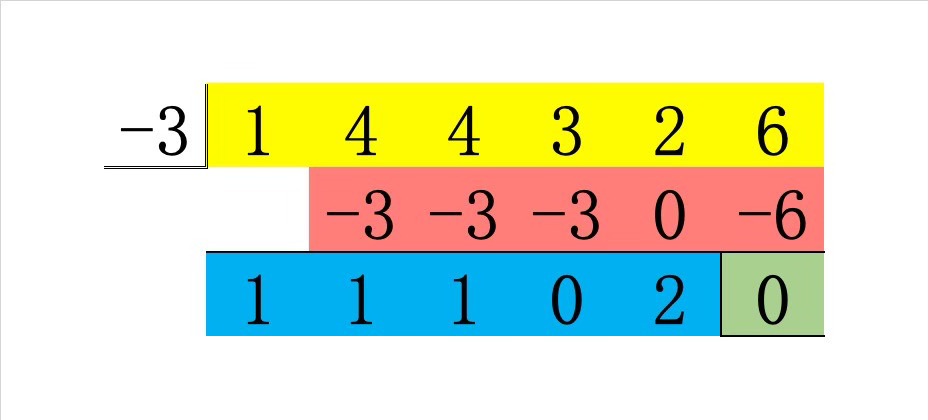
今まで見てきたように、青の部分から $$Q(x)=x^4+x^3+x^2+2$$ とおくと
P(x)+(-3Q(x))=Q(x)x
すなわち
\begin{align}
P(x)=Q(x)(x+3)
\end{align}を得ます。
これは、問にあった因数分解を
\begin{align}
P(x)=(x+3)(x^4+x^3+x^2+2)
\end{align}のように具体的に進められたことに他なりません!
因数分解の例題は こちらの記事 をどうぞ。
組立除法のココを読み取る
以上の例を見ていただければ、組立除法で計算した後の数の並びが
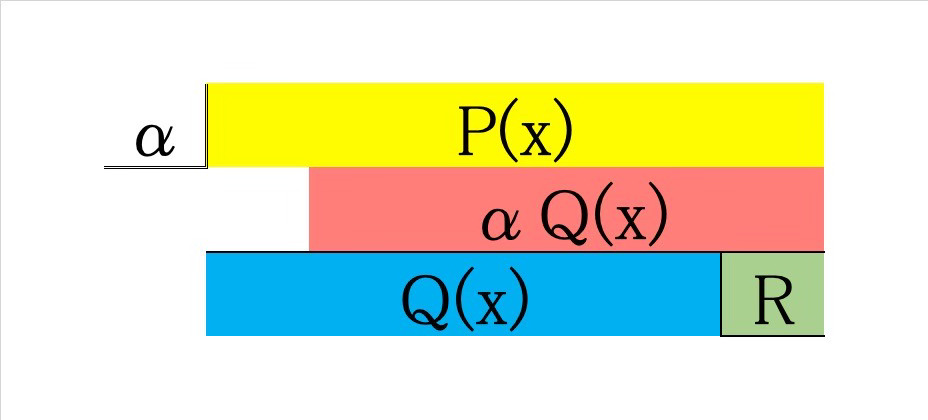
のように見えていることと思います。(私はこうなるまでに時間を要しました…。)
この関係から
P(x)+αQ(x)=Q(x)x+R
( R は緑…)となり、すなわち
\begin{align}
P(x)=Q(x)(x-\alpha)+R
\end{align}を得ます。
これは、除法の原理から \(Q(x)\) が商、\(R\) が余りを意味しますね!
以上のことから、組立除法をした後の青の部分と緑の部分(緑マーカー…)に注目するのでした。
最後に。

今回は、組立除法は筆算を簡単化したものだと知っているが腑に落ちない、納得いかない、という私のような方に向けて、筆算を用いない方法で組立除法を導き出しました。
ホーナー法を経由した方法では多項式に値を代入した結果がわかり、剰余定理から余りが求まることを見ました。
また、商が同時に求まる仕組みついても、組立除法の見え方を4つの色に分けることで補足しつつ、説明しました。
理解することが難しい事柄にぶつかったとき、異なる方向からの説明を素直に受け入れることで、元の解説も合点がいき理解が深まることがありますよね。
みなさんにとっても、この記事がそのような経験になれば嬉しいです。


コメント