 大学入試
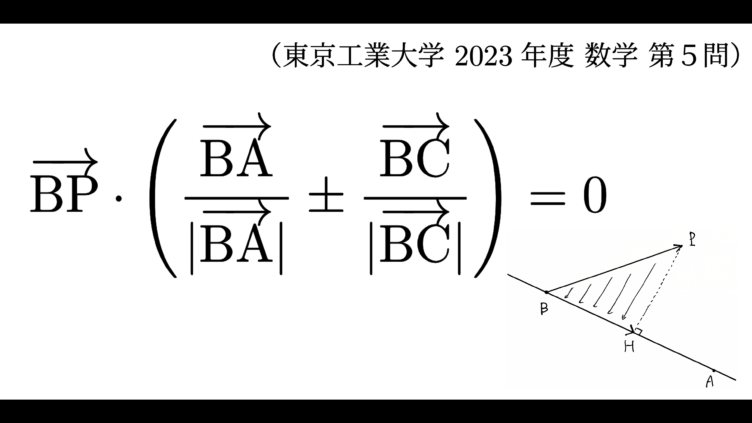
大学入試 【東京工業大学】第5問「正射影ベクトルの計算に親しもう。」解答・解説[過去問 2023年度]
2023年2月25日に実施された「東京工業大学」前期日程数学の第5問です。複数の直線から等距離にある点を決定する問題ですが、平面上であれば中学生の頃に作図した角の二等分線ですね。今回は「空間」ですが、平面の場合をヒントに解いてゆきましょう。
 大学入試
大学入試  大学入試
大学入試  数学基礎論
数学基礎論  大学入試
大学入試  大学入試
大学入試  大学入試
大学入試  高校数学+α
高校数学+α 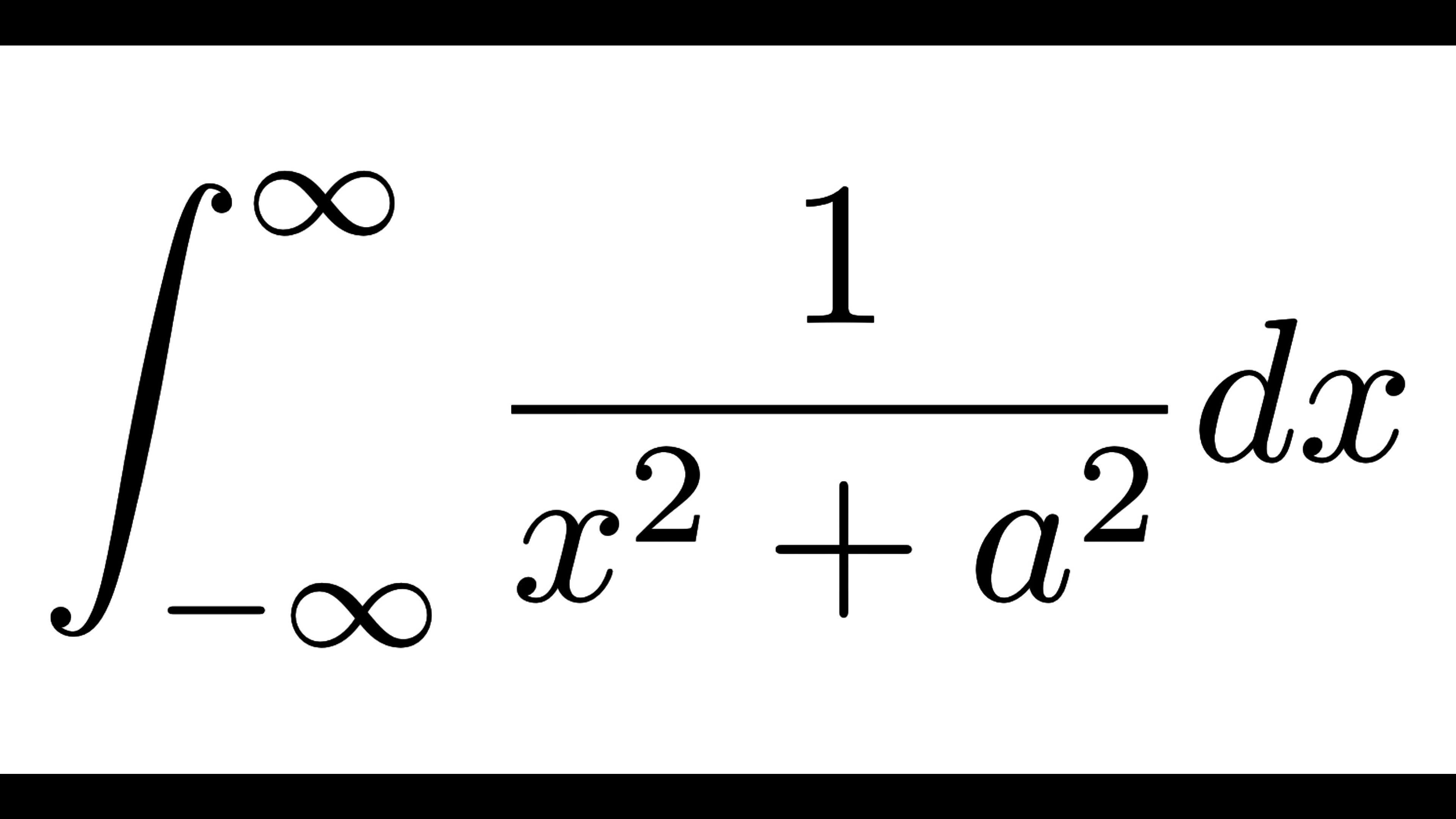 解析学系
解析学系 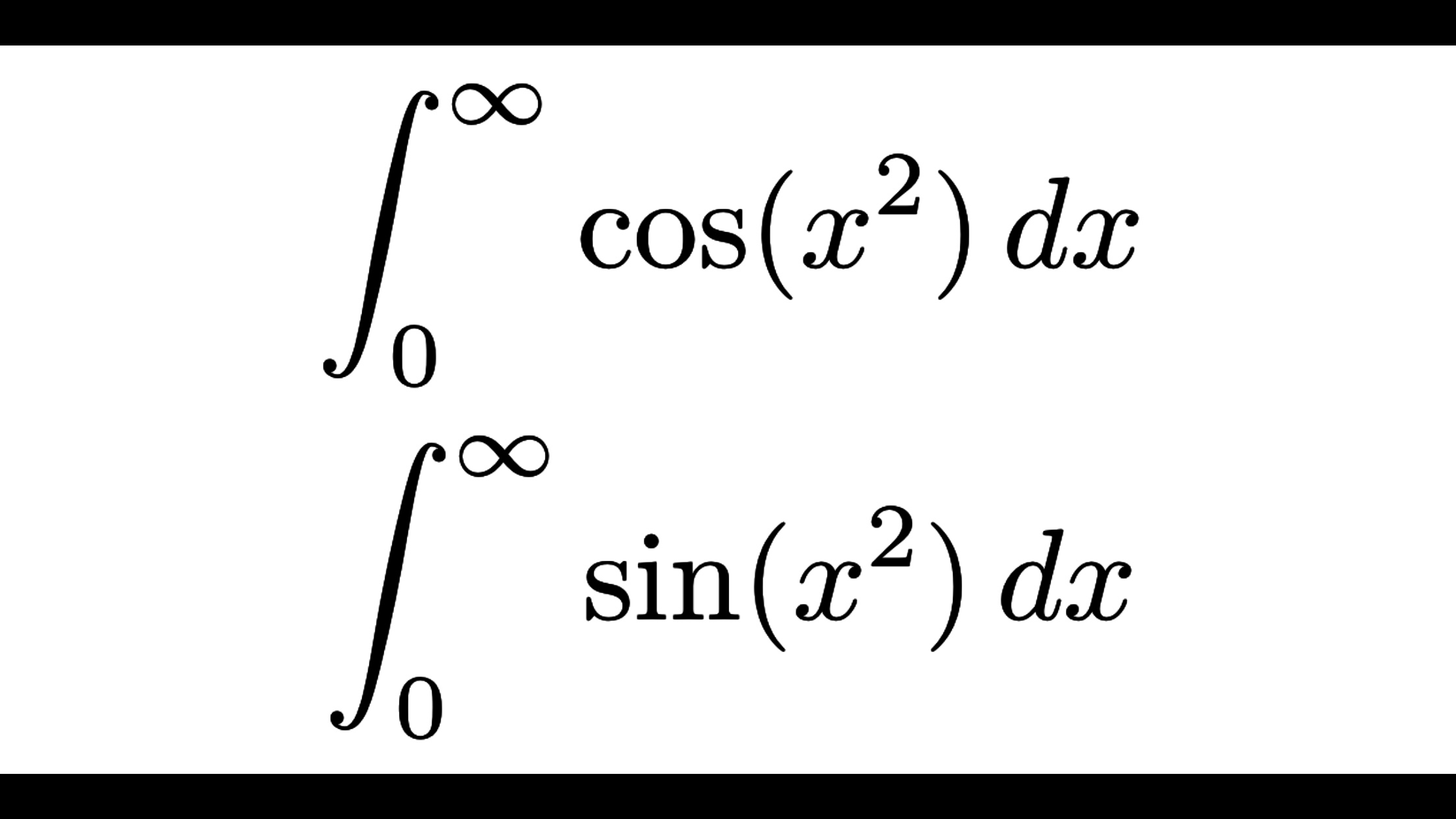 解析学系
解析学系 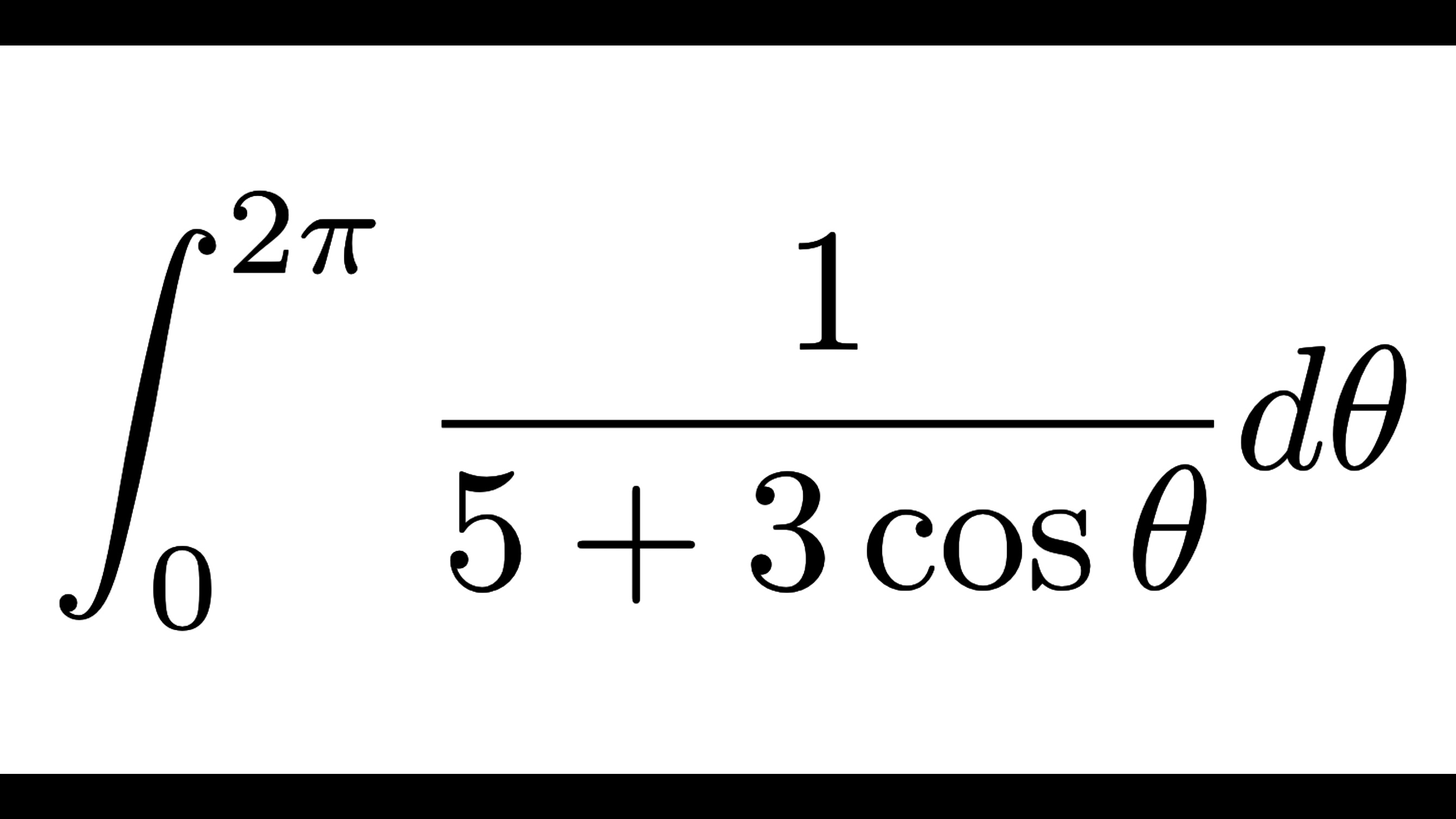 解析学系
解析学系