【数学IA】共通テスト2023 本試験 解答・解説［過去問 令和5年1月15日実施］

まず、不等式 \(|x+6|\leq2\) は $$-2\leq x+6\leq2$$ と変形できる。この各辺から \(6\) を引くことで $$-2-6\leq x\leq2-6$$ すなわち
\begin{align}
\fbox{\(-8\)}\leq x\leq\fbox{\(-4\)}\tag{1}
\end{align}を得る。

次に、不等式 \(|x+6|\leq2\) において $$x=(1-\sqrt{3})(a-b)(c-d)$$ とすると、式 (1) より
\begin{align}
-8\leq (1-\sqrt{3})(a-b)(c-d)\leq-4
\end{align}となる。この各辺に正の数 \((1+\sqrt{3})\) をかけると
\begin{align}
-8(1+\sqrt{3})\leq-2(a-b)(c-d)\leq-4(1+\sqrt{3})
\end{align}となり、各辺を \(-2\) で割ることで
\begin{align}
\fbox{\(2+2\sqrt{3}\)}\leq (a-b)(c-d)\leq \fbox{\(4+4\sqrt{3}\)}
\end{align}を得る。

今、問題文の ①、② より
\begin{align}
\begin{cases}
(a-b)(c-d)=4+4\sqrt{3}\\[5pt]
(a-c)(b-d)=-3+\sqrt{3}
\end{cases}
\end{align}すなわち
\begin{align}
\begin{cases}
ac-ad-bc+bd=4+4\sqrt{3}\\[5pt]
ab-ad-bc+cd=-3+\sqrt{3}
\end{cases}
\end{align}であるので、共通して現れる \(-ad-bc\) を消去するために第一式から第二式を引くことで
\begin{align}
ac-ab-cd+bd=7+3\sqrt{3}
\end{align}すなわち
\begin{align}
(a-d)(c-b)
&=\fbox{\(7+3\sqrt{3}\)}
\end{align}を得る。

(i)

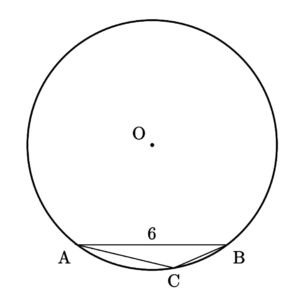
\(\triangle{\rm ABC}\) について、\({\rm AB}=6\) であって、外接円 \({\rm O}\) の半径は \(5\) である。よって、正弦定理より
\begin{align}
\sin\angle{\rm ACB}
=\frac{6}{2\times5}
=\fbox{\(\displaystyle \frac{3}{5}\)}
\end{align}となる。また、\(\angle{\rm ACB}\) が鈍角より \(\cos\angle{\rm ACB}\) は負である。よって、$$1-\left(\frac{3}{5}\right)^2=\frac{5^2-3^2}{5^2}=\frac{4^2}{5^2}$$ より
\begin{align}
\cos\angle{\rm ACB}=\fbox{\(\displaystyle -\frac{4}{5}\)}
\end{align}を得る。

(ii)

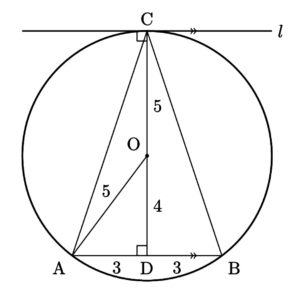
\(\triangle{\rm ABC}\) の面積が最大になるのは、直線 \({\rm AB}\) と点 \({\rm C}\) の距離 \({\rm CD}\) が最大になるときであって、それは点 \({\rm C}\) における円 \({\rm O}\) の接線 \(l\) が直線 \({\rm AB}\) と平行になるときである。このとき、直線 \({\rm CD}\) は接線 \(l\) と直交するので、円 \({\rm O}\) の中心を通り、線分 \({\rm AB}\) を垂直に二等分する。

よって、\(\triangle{\rm OAD}\) は \(\angle{\rm ODA}=90^\circ\) の直角三角形で、\({\rm OA}=5\) かつ \({\rm AD}=3\) なので、三平方の定理より $${\rm OD}=\sqrt{5^2-3^2}=4$$ である。これより、
\begin{align}
\tan\angle{\rm OAD}=\frac{\rm OD}{\rm AD}=\fbox{\(\displaystyle \frac{4}{3}\)}
\end{align}となる。このとき、\(\triangle{\rm ABC}\) の面積は
\begin{align}
{\rm AB}\times{\rm CD}\times\frac{1}{2}
&=6\times(5+4)\times\frac{1}{2}\\
&=\fbox{\(27\)}
\end{align}である。

まず、\(\triangle{\rm PQR}\) において、余弦定理より
\begin{align}
\cos\angle{\rm QPR}=\frac{8^2+9^2-5^2}{2\times8\times9}=\fbox{\(\displaystyle \frac{5}{6}\)}
\end{align}となる。ここで、\(\triangle{\rm PQR}\) の面積を求めるために \(\sin\angle{\rm QPR}\) を計算すると
\begin{align}
1-\left(\frac{5}{6}\right)^2=\frac{6^2-5^2}{6^2}=\frac{11}{6^2}
\end{align}より \(\displaystyle \sin\angle{\rm QPR}=\frac{\sqrt{11}}{6}\) である。これより、\(\triangle{\rm PQR}\) の面積は
\begin{align}
\frac{1}{2}\times{\rm PQ}\times{\rm PR}\times\sin\angle{\rm QPR}
&=\frac{1}{2}\times8\times9\times\frac{\sqrt{11}}{6}\\
&=\fbox{\(6\sqrt{11}\)}
\end{align}である。

次に、三角錐 \({\rm TPQR}\) の体積が最大になるのは、平面 \(\alpha\) と点 \({\rm T}\) の距離 \({\rm TH}\) が最大になるときであって、それは点 \({\rm T}\) において球 \({\rm S}\) に接する平面 \(\beta\) が平面 \(\alpha\) と平行になることを意味する。このとき、直線 \({\rm TH}\) は平面 \(\beta\) と直交するので、球 \({\rm S}\) の中心を通り、点 \({\rm H}\) は \(\triangle{\rm PQR}\) の外心となる。

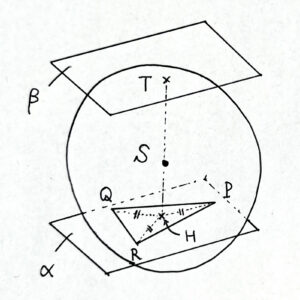
これより、\({\rm PH}\), \({\rm QH}\), \({\rm RH}\) は全て \(\triangle{\rm PQR}\) の外接円の半径であることから互いに等しく
\begin{align}
\fbox{\({\rm PH}={\rm QH}={\rm RH}\)}
\end{align}である。ここで、\(\triangle{\rm PQR}\) において、\({\rm PH}\) が概説園の半径であることに注意すれば、正弦定理より
\begin{align}
{\rm PH}=\frac{\rm QR}{2\sin\angle{\rm QPR}}=\frac{15}{\sqrt{11}}
\end{align}である。球 \(S\) の半径は \(5\) なので、\(\triangle{\rm SPH}\) において三平方の定理より $${\rm SH}=\sqrt{5^2-\frac{15^2}{11}}=\frac{5\sqrt{2}}{\sqrt{11}}$$ である。このとき、三角錐 \(\triangle{\rm TPQR}\) の体積は
\begin{align}
\triangle{\rm PQR}\times{\rm TH}\times\frac{1}{3}
&=6\sqrt{11}\times\left(5+\frac{5\sqrt{2}}{\sqrt{11}}\right)\times\frac{1}{3}\\
&=\fbox{\(10\left(\sqrt{11}+\sqrt{2}\right)\)}
\end{align}となる。

全部で \(52\) 市あるので、第１四分位数は下位から \(13\) 番目の市と \(14\) 番目の市の平均であり、両市共に \(1800\) 以上 \(2200\) 未満の階級に含まれる。よって、第１四分位数は \(\fbox{1800 以上 2200 未満}\) である。

同様に、第３四分位数は上位から \(13\) 番目の市と \(14\) 番目の平均の市であって、両市共に \(3000\) 以上 \(3400\) 未満の階級に含まれる。よって、第３四分位数は \(\fbox{3000 以上 3400 未満}\) である。

四分位範囲は上記のふたつの四分位数の差で求まるので、
\begin{align}
3000-2200&=800,\\
3400-1800&=1600
\end{align}より \(\fbox{800 より大きく 1600 より小さい}\) ことがわかる。

(i)

• 地域Eは \(19\) 市あるので、第１四分位数は下位から \(5\) 番目であるが、箱ひげ図より \(2000\) を超えているので ⓪ は誤り。
• 箱ひげ図のひげの長さが異なるため ① 誤り。
• 箱ひげ図の箱の中央の線を見ると \(\fbox{ ② は正しい}\) 。
• 地域Eは \(19\) 市なので第３四分位数は下位から \(15\) 番目であって、\(2600\) 未満の市は \(14\) 市以下であることはわかる。一方、地域Wは \(33\) 市なので中央値は下位から \(17\) 番目であって、\(2600\) 未満の市は \(16\) 市以下であることはわかる。これだけで ③ が正しいとは言い切れない。

(ii)

データを分析する際の「分散」とは、偏差の \(2\) 乗の平均であるので \(\fbox{ ② が正しい}\) 。

対になっているのデータを分析する際の「相関係数」とは、共分散を各々の標準偏差で割った値である。よって、相関係数は
\begin{align}
\frac{124000}{590\times570}
&=\frac{1240}{59\times57}\\
&=\frac{1240}{3363}\\
&=0.368\cdots
\end{align}であるので \(\fbox{ ⑦ }\) である。

放物線 \(C_1\) は、\(x=0,4\) のとき \(y=3\) となる。よって、\(y=ax(x-4)+3\) すなわち $$y=\fbox{\(ax^2-4ax+3\)}$$ と書ける。放物線 \(C_1\) は上に凸であって左右対称な曲線であるので、\(x=2\) を代入することで、プロ選手のシュートの高さは $$\fbox{\(-4a+3\)}$$ となる。

放物線 \(C_2\) の方程式は

$$y=p\left\{x-\left(2-\frac{1}{8p}\right)\right\}^2-\frac{(16p-1)^2}{64p}+2$$

であって、上に凸であることから \(p<0\) である。よって、放物線 \(C_2\) の頂点の \(x\) 座標はについて $$2-\frac{1}{8p}>2$$ が成り立つ。これより、\(\fbox{ ② }\) である。

点 \({\rm D}\) の座標は \(\displaystyle \left(\frac{19}{5}, 3+\frac{\sqrt{3}}{15}\right)\) であるので、方程式 \(y=ax(x-4)+3\) に代入すると
\begin{align}
3+\frac{\sqrt{3}}{15}&=a\times\frac{19}{5}\times\left(-\frac{1}{5}\right)+3\\
\frac{\sqrt{3}}{15}&=a\times\frac{19}{5}\times\left(-\frac{1}{5}\right)
\end{align}となるので \(\displaystyle a=-\frac{5\sqrt{3}}{57}\) より

$$y=\fbox{\(\displaystyle -\frac{5\sqrt{3}}{57}\)}\ (x^2-4x)+3$$

となる。

プロ選手のシュートの高さ \(-4a+3\) より

\begin{align}
\frac{20\sqrt{3}}{57}+3
&=\frac{20\times1.732\cdots}{57}+3\\
&=\frac{34.64\cdots}{57}+3\\
&=0.6077\cdots+3\\
&=3.6077\cdots
\end{align}

である。花子さんのシュートの高さは約 \(3.4\) で、プロ選手のシュートの高さは約 \(3.6\) である。よって、\(\fbox{プロ選手}\) の高さ方が約 \(0.2\) だけ、すなわち \(\fbox{ボール約 \(1\) 個分}\) 大きい。

• 球1は \(5\) 通り。
• 球2は球1と異なる \(4\) 通り。
• 球3は球2と異なる \(4\) 通り。
• 球4は球3と異なる \(4\) 通り。

よって、\(5\times4^3=\fbox{\(320\)}\) 通りである。

• 球1は \(5\) 通り。
• 球2は球1と異なる \(4\) 通り。
• 球3は球1と球2とも異なる \(3\) 通り。

よって、\(5\times4\times3=\fbox{\(60\)}\) 通りである。

紐で繋がっていない球が赤で塗られるときのみ考えれば良く、球は \({1,3}\), \({2,4}\) の \(2\) 通りの選び方がある。

残りの \(2\) 個の球は赤以外の \(4\) 色で独立に塗るため \(4\times4\) 通り。

よって、\(2\times4\times4=\fbox{\(32\)}\) 通りである。

球1に塗った色は他の球に塗ることができないので、球2から球6の \(5\) 個のうち \(3\) 個を赤に、\(2\) 個を青に塗ることになり、それは \({}_5{\rm C}_2=10\) 通り。

球1は、赤と青以外の \(3\) 色から \(1\) 色だけ選んで塗るので \(3\) 通り。

よって、\(10\times3=\fbox{\(30\)}\) 通りである。

球3と球4が一体化したものと解釈すれば良いので、\(3\) 個の球を輪っか状に繋げた \(\fbox{2}\) に一致する。

よって、(1)の図Bの場合の総数 \(320\) から (2)の図Cの場合の総数 \(60\) を除けば良いので、\(320-60=\fbox{\(260\)}\) 通りである。

(5)と同様に考える。

球4と球5を切り離したものと解釈すると、\(5\) 個の球を一列に繋げた場合の総数 \(5\times4^4=1280\) を得る。

球4と球5が一体化したものと解釈すると、\(4\) 個の球を輪っか状に繋げた (5)の図Dの場合の総数 \(260\) を得る。

よって、切り離した場合の総数 \(1280\) から一体化した場合の総数 \(260\) を除けば良いので、\(1280-260=\fbox{\(1020\)}\) 通りである。

\(110=2\times5\times11\) と素因数分解できて、素数 \(11\) は \(462\) を割り切るので \(\fbox{\(11\)}\) である。

また、\(462=2\times3\times7\times11\) である。\(110\) と \(462\) の最小公倍数を考えれば良いので、一辺の長さは、\(110\) にはあるが \(462\) にはない素因数を補って \(462\times5=\fbox{\(2310\)}\) となる。

縦に \(x\) 枚、横に \(y\) 枚だけ並べたとする。縦と横の長さの差の絶対値は、最大公約数で括ることで $$|110x-462y|=22|5x-21y|$$ と書ける。ここで、例えば \((x,y)=(4,1)\) とすると最小の \(\fbox{\(22\)}\) をとる。

縦の方が横より長いので、不定方程式 $$5x-21y=1$$ の正の整数の解を考えることになる。\(y\) が最小の解を見つければ良いので、例えば $$5x=21y+1=5\times4y+(y+1)$$ と変形することで \((y+1)\) が \(5\) の倍数である必要があることがわかる。実際、最小の正の \(5\) の倍数になる \(y+1=5\) を確認すると、$$(x,y)=(17,4)$$ であって、横の長さは \(462\times4=\fbox{\(1848\)}\) である。

縦の長さを比較すると \(110=2\times5\times11\) と \(154=2\times7\times11\) であるので、最小公倍数を考えることで、最小の縦の長さは \(154\times5=\fbox{\(770\)}\) であることがわかる。

横の長さを比較すると \(462=2\times3\times7\times11\) と \(363=3\times11^2\) であるので、最大公約数は \(3\times11=\fbox{\(33\)}\) である。

さらに、\(33=3\times11\) であって \(770=11\times70\) であるので、これらの最小公倍数は \(3\times11\times70=\fbox{\(2310\)}\) である。

赤と青の長方形を横にそれぞれ \(a\) 枚、\(b\) 枚だけ並べたとすると、一辺の長さは $$462a+363b=33(14a+11b)$$ である。これが \(2310\) の倍数となるので、正の整数 \(n\) を用いて \(2310n\) と書くと $$14a+11b=70n$$ を得る。

縦の長さは、正の \(770\) の倍数は全てとることができるので、横の長さが \(2310=770\times3\) の倍数になれば、新たに条件を課すことなく正方形が作れる。

ここで、\(11b\) は \(14\) の倍数である必要があるので、\(11\) と \(14\) が互いに素であることから最小の \(b=14\) を採用する。このとき、$$a+11=5n$$ であるので \((a+11)\) は \(5\) の倍数であり、最小の正の整数 \(a\) として \(a=4\) を採用する。これより、\(n=3\) であるので、一辺の長さは \(2310\times3=\fbox{\(6930\)}\) である。

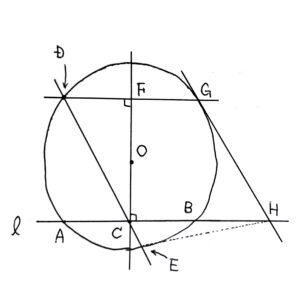
示したいのは $$\angle{\rm OEH}=\fbox{\(90\)}\ {}^\circ$$ である。

ここで、\(\angle{\rm HCO}=\angle{\rm HGO}=90^\circ\) であるので、\(4\) 点 \({\rm C}, {\rm G}, {\rm H}, \fbox{\({\rm O}\)}\) は線分 \({\rm OH}\) を直径とする同一円周上に存在する。

よって、円に内接する四角形の対角を考えることで $$\angle{\rm CHG}+\angle{\rm COG}=180^\circ$$ であるので、\(\angle{\rm COG}\) の外角を考えることによって $$\angle{\rm CHG}=\fbox{\(\angle{\rm FOG}\)}$$ となる。

また、二等辺三角形 \({\rm ODG}\) の頂角に対して円周角の定理を考えることで $$\angle{\rm FOG}=\frac{1}{2}\angle{\rm DOG}=\fbox{\(\angle{\rm DEG}\)}$$ を得る。

よって、\(\angle{\rm CHG}=\angle{\rm CEG}\) であるので、円周角の定理の逆より \(4\) 点 \({\rm C}, {\rm G}, {\rm H}, \fbox{\({\rm E}\)}\) は同一円周上に存在する。この円は線分 \({\rm OH}\) を直径とする円であったので、\(\angle{\rm OEH}=90^\circ\) を得る。

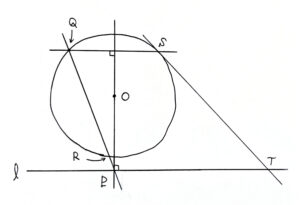
(1)と同様に、\(4\) 点 \({\rm P}, {\rm S}, {\rm T}, {\rm O}\) は線分 \({\rm OT}\) を直径とする同一円周上に存在する。よって、\(\angle{\rm PTS}\) は \(\angle{\rm POS}\) の外角に等しく、二等辺三角形 \({\rm OQS}\) の頂角に対して円周角の定理を考えることで $$\angle{\rm PTS}=\fbox{\(\angle{\rm QRS}\)}$$ を得る。

よって、四角形の向かい合う角 \(\angle{\rm PRS}\) と \(\angle{\rm PTS}\) の和が \(180^\circ\) なので、\(5\) 点 \({\rm P}, {\rm R}, {\rm S}, {\rm T}, {\rm O}\) は同一円周上に存在する。この円は線分 \({\rm OT}\) を直径とする円であったので、与えられた \({\rm OT}=3\sqrt{6}\) より半径は \(\fbox{\(\displaystyle \frac{3\sqrt{6}}{2}\)}\) である。

また、\(\triangle{\rm ORT}\) において三平方の定理を考えることで $${\rm RT}=\sqrt{{\rm OT}^2-{\rm OR}^2}=\fbox{\(7\)}$$ を得る。