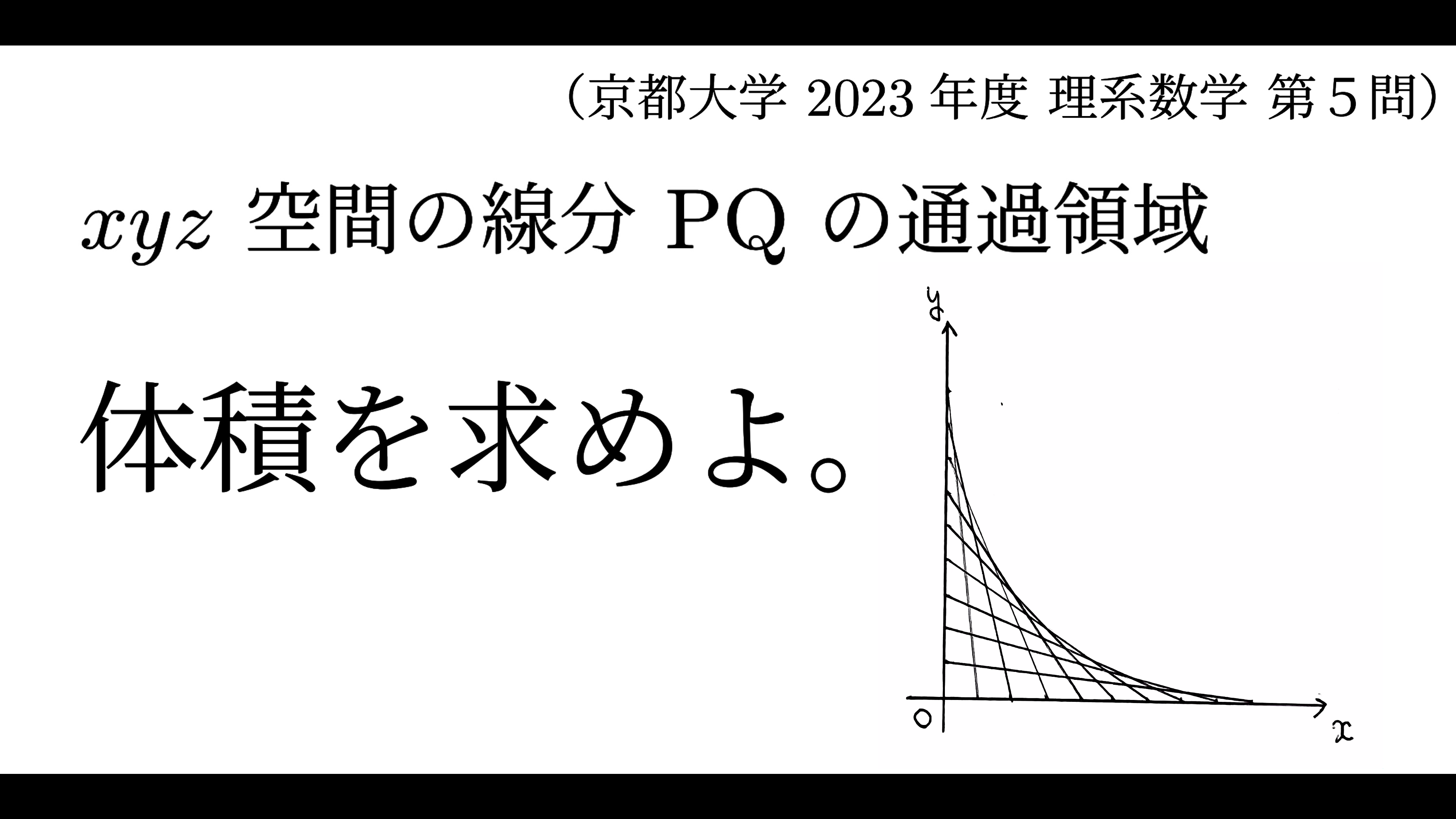
\({\rm O}\) を原点とする \(xyz\) 空間において、点 \({\rm P}\) と点 \({\rm Q}\) は次の \(3\) つの条件 (a),(b),(c) を満たしている。
(a) 点 \({\rm P}\) は \(x\) 軸上にある。
(b) 点 \({\rm Q}\) は \(yz\) 平面上にある。
(c) 線分 \({\rm OP}\) と線分 \({\rm OQ}\) の長さの和は \(1\) である。
点 \({\rm P}\) と点 \({\rm Q}\) が条件 (a),(b),(c) を満たしながらくまなく動くとき、線分 \({\rm PQ}\) が通過してできる立体の体積を求めよ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】

点 \({\rm P}\) は条件(a)と条件(c)によって動く範囲が決まるが、点 \({\rm Q}\) を固定すると \(x\) 軸上の原点 \({\rm O}\) に関して対称な位置に存在し得る。
点 \({\rm Q}\) は条件(b)と条件(c)によって動く範囲が決まるが、点 \({\rm P}\) を固定すると \(yz\) 平面上の原点 \({\rm O}\) を中心とする一つの円周上に存在し得る。
ここで、点 \({\rm P}\) を \(x\) 軸上の \(x\geq0\) の部分、点 \({\rm Q}\) を \(y\) 軸上の \(y\geq0\) の部分に制限して線分 \({\rm PQ}\) の通過領域を考える。その領域を \(x\) 軸を中心に回転させ、回転体を \(yz\) 平面に関して対称移動したものが体積を求める立体となる。
以下、\(xy\) 平面のみを考える。
\({\rm P}(t,0)\) (\(0\leq t\leq 1\)) とおくと \({\rm Q}(0,1-t)\) となるので、直線 \({\rm PQ}\) の方程式は $$(1-t)x+ty=t(1-t)$$ と書ける。

まず、\(0<t\leq 1\) のとき、直線 \({\rm PQ}\) の方程式を \(t\) に関して整理すると $$y=x+1-t-\frac{x}{t}$$ である。点 \({\rm Q}\) を除く線分 \({\rm PQ}\) 上の点 \((x,y)\) について \(0<x\leq t\leq 1\) であるので、相加平均と相乗平均の大小関係より
\begin{align}
y
&\leq x+1-2\sqrt{t\times\frac{x}{t}}\\
&= x+1-2\sqrt{x}\\
&= (1-\sqrt{x})^2\tag{1}
\end{align}となる。但し、\(t=\sqrt{x}\) のとき等号が成り立つ。
次に、\(t=0\) のとき \({\rm P}(0,0)\) かつ \({\rm Q}(0,1)\) であるので、不等式 (1) は点 \({\rm Q}\) を含めた場合、すなわち、\(x=0\) のときも成り立つ。
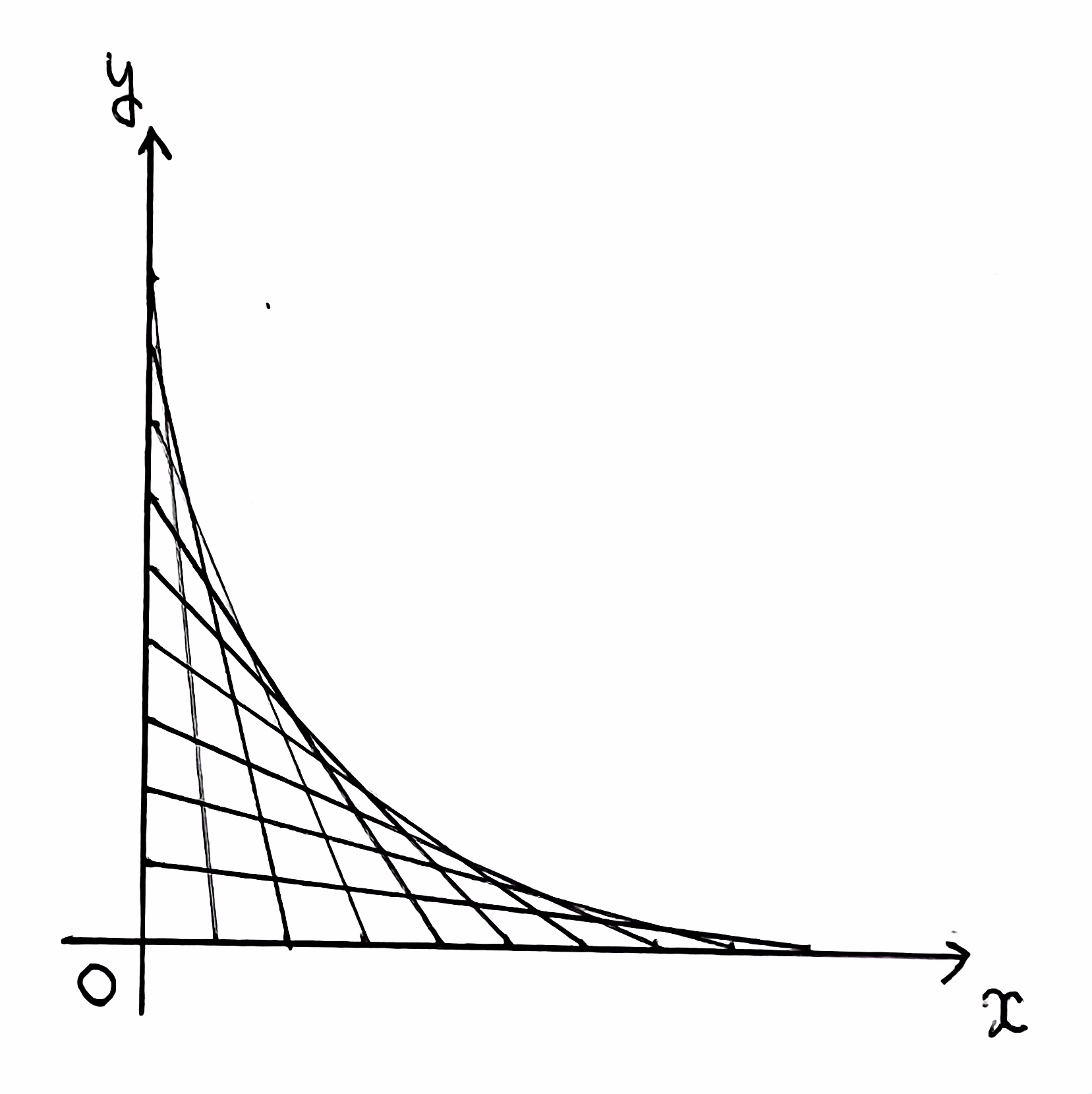
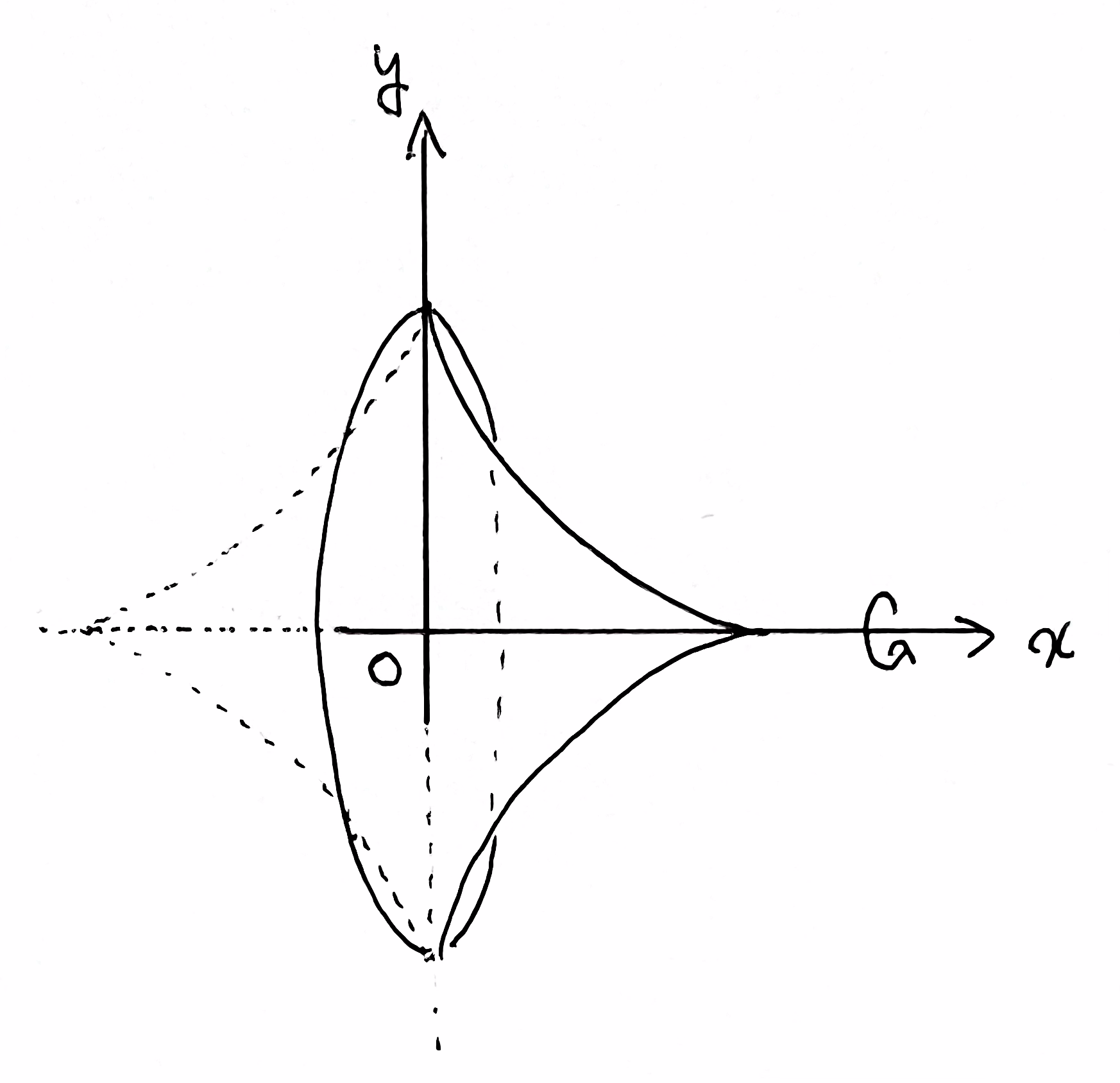
以上より、求める体積は
\begin{align}
&\pi\int_0^1 \left\{(1-\sqrt{x})^2\right\}^2 dx\times2\\
&\quad=2\pi\int_0^1 (1-\sqrt{x})^4 dx\\
&\quad=2\pi\int_0^1 (1-4\sqrt{x}+6x-4x\sqrt{x}+x^2) dx\\
&\quad=2\pi\left(1-\frac{8}{3}+3-\frac{8}{5}+\frac{1}{3}\right)\\
&\quad=\frac{2}{15}\pi
\end{align}
となる。
考察と感想

条件の対称性から、点 \({\rm P}\) を \(x\) 軸上の \(x\geq0\) の部分、点 \({\rm Q}\) を \(y\) 軸上の \(y\geq0\) の部分に制限して線分 \({\rm PQ}\) の通過領域を考えました。
グラフの通過領域に関する問題は、今回のように \(x\) を固定して \(t\) の変化に対する値域を調べたりします。他にも、解の存在条件・配置の問題として解く考え方もあります。
その領域を \(x\) 軸を中心に回転させた 回転体 を考え、体積を \(2\) 倍すれば良いです。あとは、積分の計算をミスなく落ち着いて行います。
コメント