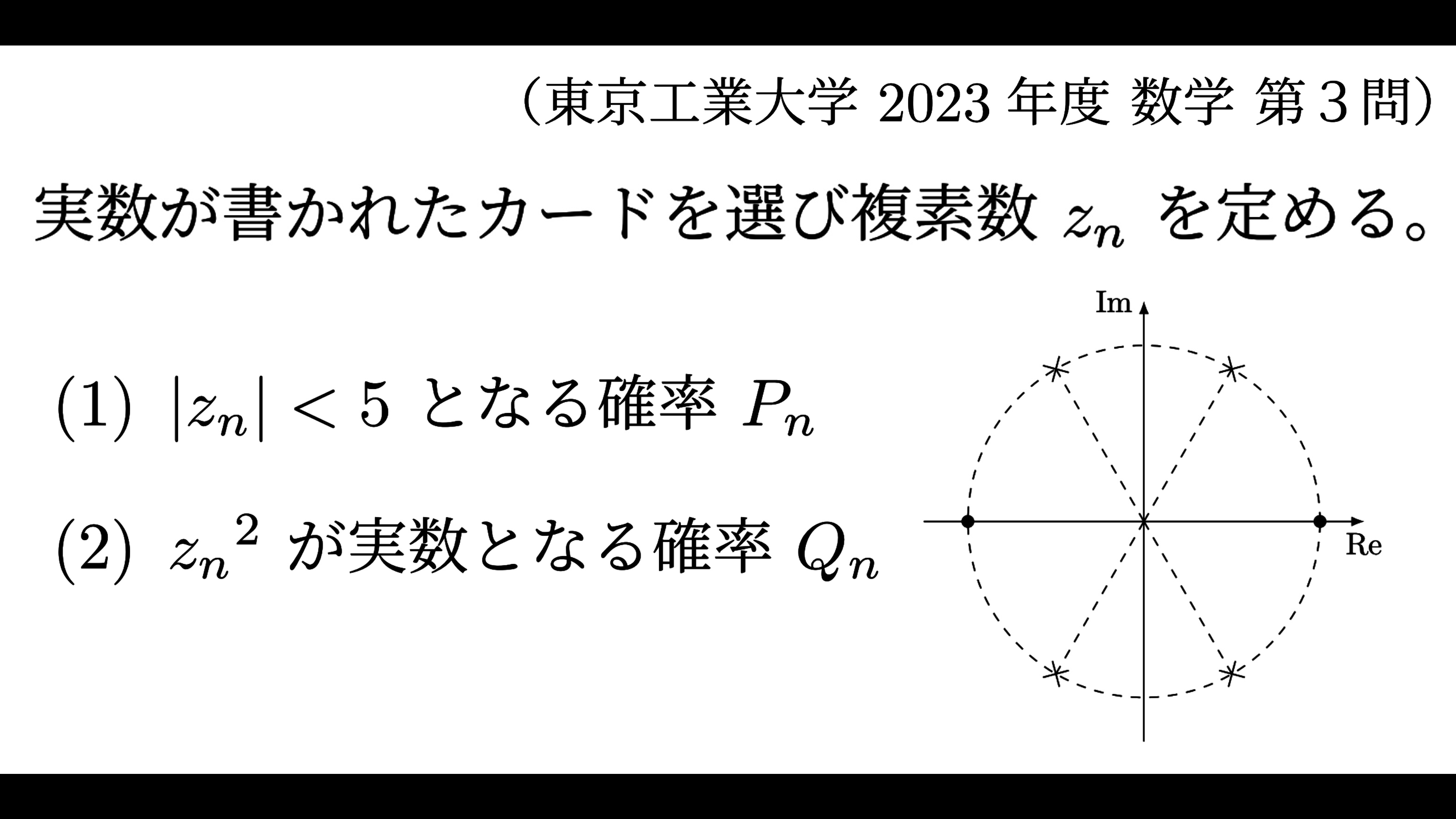
実数が書かれたカード \(\fbox{\(0\)}\) , \(\fbox{\(1\)}\) , \(\fbox{\(\sqrt{3}\)}\) から、無作為に \(2\) 枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数 \(n\) に対して、この操作を \(n\) 回繰り返して得られる \(n\) 個の複素数の積を \(z_n\) で表す。
(1)\(|z_n|<5\) となる確率 \(P_n\) を求めよ。
(2)\({z_n}^2\) が実数となる確率 \(Q_n\) を求めよ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】

(1)
絶対値を考えるので、各操作で実部と虚部に選ばれるカードは入れ替えても良い。
各操作において
| 選ぶカード | 確率 | (絶対値)\({}^2\) |
| \(A=\Bigl\{\fbox{\(0\)},\ \fbox{\(1\)}\Bigr\}\) | \(\displaystyle \frac{1}{3}\) | \(1\) |
| \(B=\Bigl\{\fbox{\(0\)},\ \fbox{\(\sqrt{3}\)}\Bigr\}\) | \(\displaystyle \frac{1}{3}\) | \(3\) |
| \(C=\Bigl\{\fbox{\(1\)},\ \fbox{\(\sqrt{3}\)}\Bigr\}\) | \(\displaystyle \frac{1}{3}\) | \(4\) |
であるので、条件 \(|{z_n}|<5\) すなわち $$|{z_n}|^2<25$$ を満たすのは「\(B\) から選ぶときと \(C\) から選ぶときが合わせて \(2\) 回以下である場合」となる。
よって、\(n\geq2\) として、その回数 \(k\) を小さい順に考えると
\begin{align}
P_n
&=\sum_{k=0}^2{}_n{\rm C}_k\left(\frac{2}{3}\right)^k\left(\frac{1}{3}\right)^{n-k}\\
&=\frac{1+n\times2+\frac{n(n-1)}{2}\times2^2}{3^n}\\
&=\frac{2n^2+1}{3^n}
\end{align}となる。
これは \(n=1\) のときも成り立つので $$P_n=\frac{2n^2+1}{3^n}$$ である。
(2)
複素数が実数であることは偏角の値で判断できる。
各操作において
| 作られる複素数 | 確率 | (偏角)\(\times2\) |
| \(\fbox{\(\ast\)}+\fbox{\(0\)}\ i\) | \(\displaystyle \frac{1}{3}\) | \(0^\circ=60^\circ\times0\) |
| \(\fbox{\(0\)}+\fbox{\(\ast\)}\ i\) | \(\displaystyle \frac{1}{3}\) | \(180^\circ=60^\circ\times3\) |
| \(\fbox{\(\sqrt{3}\)}+\fbox{\(1\)}\ i\) | \(\displaystyle \frac{1}{6}\) | \(60^\circ=60^\circ\times1\) |
| \(\fbox{\(1\)}+\fbox{\(\sqrt{3}\)}\ i\) | \(\displaystyle \frac{1}{6}\) | \(120^\circ=60^\circ\times2\) |
である。
原点を中心とした適当な半径(\(|z_n|^2\) や \(|z_{n+1}|^2\))の円周を、以下のように複素数平面上で考える。このとき、求めたい \(Q_n\) は \({z_n}^2\) が \(\bullet\) にある確率である。
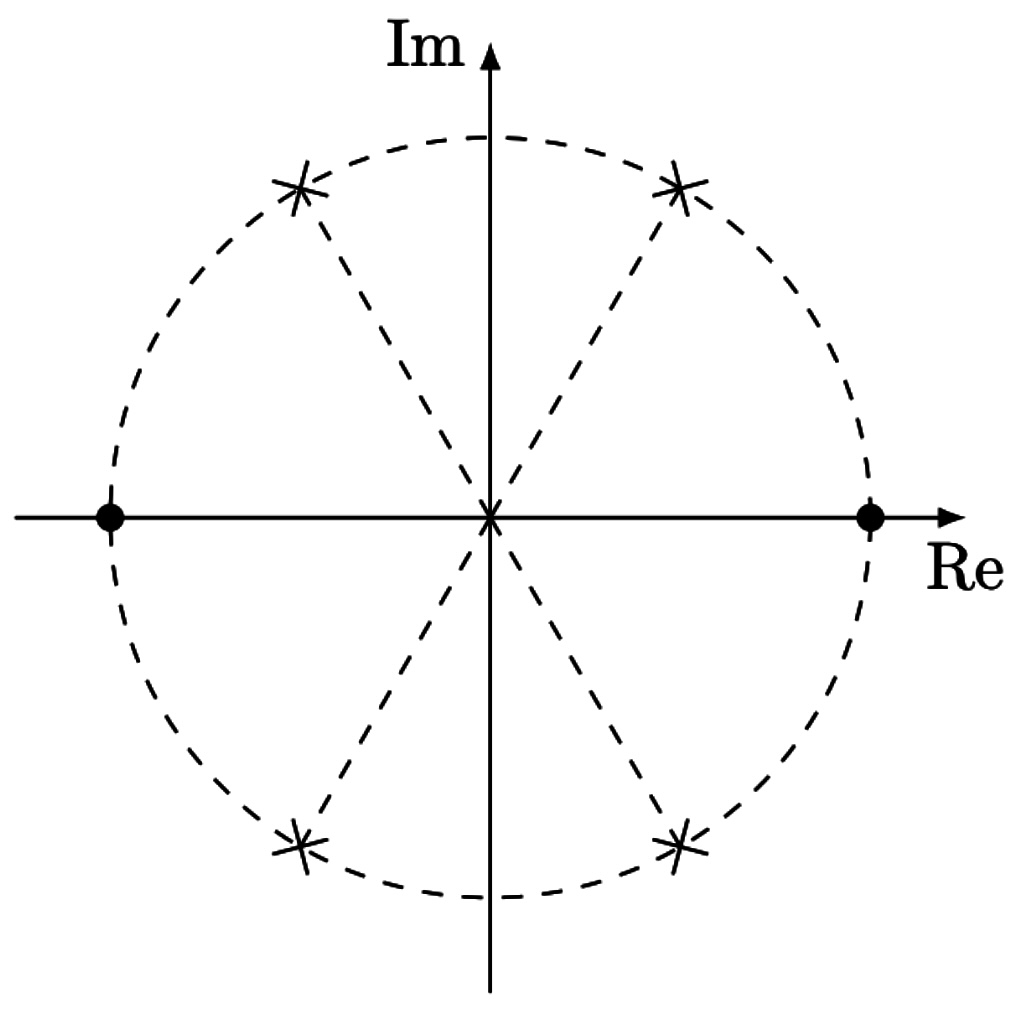
ここで、\({z_n}^2\) からもう一度操作をして \({z_{n+1}}^2\) を作ったとき
- 複素数が \(\times\ \longrightarrow\ \bullet\) と移る確率は \(\displaystyle \frac{1}{6}\)
- 複素数が \(\bullet\ \longrightarrow\ \bullet\) と移る確率は \(\displaystyle \frac{2}{3}\)
である。
今、\({z_n}^2\) が \(\times\) にある確率は \(1-Q_n\) なので
\begin{align}
Q_{n+1}
&=(1-Q_n)\times\frac{1}{6}+Q_n\times\frac{2}{3}\\
&=\frac{1}{2}Q_n+\frac{1}{6}
\end{align}すなわち $$Q_{n+1}-\frac{1}{3}=\frac{1}{2}\left(Q_n-\frac{1}{3}\right)$$ である。
さて、$$Q_1-\frac{1}{3}=\frac{2}{3}-\frac{1}{3}=\frac{1}{3}$$ であるので
\begin{align}
Q_n
&=\frac{1}{3}+\frac{1}{3}\times\left(\frac{1}{2}\right)^{n-1}\\
&=\frac{1}{3}\left\{1+\left(\frac{1}{2}\right)^{n-1}\right\}
\end{align}である。
考察と感想

(1)について
(1)の条件を満たすかは 絶対値 のみ考えれば良く、偏角は関係ないです。特に、今回は条件の判定がしやすいように、絶対値の \(2\) 乗について表にまとめました。表中の \(A\) の場合は絶対値を変えないので \(B\) と \(C\) の場合を考えますが、結局、それらを合わせて \(2\) 回までということがわかります。よって、それらの確率を合わせた \(\displaystyle \frac{2}{3}\) が \(2\) 乗まで現れる二項展開のようなものを考えます。
(2)について
一方、(2)は 偏角 のみで、絶対値は関係ありません。特に、今回は偏角の \(2\) 倍を加えてゆくことになります。表にまとめてみると、偏角は \(60^\circ\) の整数倍であったので、複素数平面に円周を \(6\) 等分したものを書きました。条件を満たす点 \(\bullet\) が \(2\) 箇所で、満たさない点 \(\times\) が \(4\) 箇所なので $$\lim_{n\to\infty}Q_n=\frac{2}{2+4}=\frac{1}{3}$$ であろうと予想されます。実際に、点の移り変わりから漸化式を立て、解いてゆくと…。

コメント