\(a\) を実数とし、座標平面上の点 \((0,a)\) を中心とする半径 \(1\) の円の周を \(C\) とする。
(1)\(C\) が、不等式 \(y>x^2\) の表す領域に含まれるような \(a\) の範囲を求めよ。
(2)\(a\) は(1)で求めた範囲にあるとする。\(C\) のうち、\(x\geq0\) かつ \(y<a\) を満たす部分を \(S\) とする。\(S\) 上の点 \({\rm P}\) に対し、点 \({\rm P}\) での \(C\) の接線が放物線 \(y=x^2\) によって切り取られてできる線分の長さを \(L_{\rm P}\) とする。\(L_{\rm Q}=L_{\rm R}\) となる \(S\) 上の相異なる \(2\) 点 \({\rm Q}\),\({\rm R}\) が存在するような \(a\) の範囲を求めよ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】

(1)
\(C\) 上の点は、\(0\leq\theta<2\pi\) なる実数 \(\theta\) を用いて
\begin{align}
(\cos\theta,a+\sin\theta)
\end{align}と書ける。
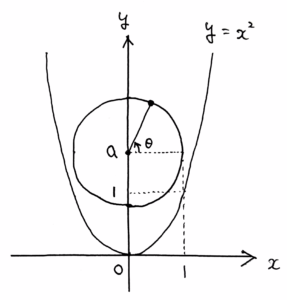
これが領域 \(y>x^2\) に含まれるのは \(a+\sin\theta>\cos^2\theta\) となるとき。よって、
\begin{gather}
a+\sin\theta>\cos^2\theta\\
a+\sin\theta>1-\sin^2\theta\\
\sin^2\theta+\sin\theta+a-1>0\\
(2\sin\theta+1)^2>5-4a
\end{gather}となる。これが \(-1\leq\sin\theta\leq1\) で常に成り立つのは \(5-4a<0\) すなわち \(\displaystyle a>\frac{5}{4}\) のときである。
(2)
\(S\) 上の点 \({\rm P}\) は、\(\displaystyle 0<\theta\leq\frac{\pi}{2}\) なる実数 \(\theta\) を用いて
\begin{align}
{\rm P}(\cos\theta,a-\sin\theta)
\end{align}と書ける。
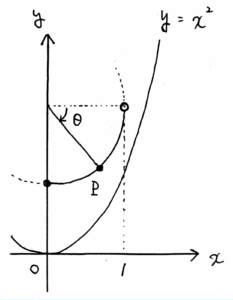
また、この点 \({\rm P}\) における \(C\) の接線 \(l_{\rm P}\) の方程式は
\begin{align}
(\cos\theta)x-(\sin\theta)y=1-a\sin\theta
\end{align}と書ける。ここで、\(y=x^2\) とすると
\begin{align}
(\cos\theta)x-(\sin\theta)x^2&=1-a\sin\theta
\end{align}すなわち
\begin{align}
(\sin\theta)x^2-(\cos\theta)x+(1-a\sin\theta)&=0
\end{align}
となる。今、\(0<\sin\theta\leq1\) である。
(1)より、この \(x\) の \(2\) 次方程式は異なるふたつの実数解 \(\alpha\),\(\beta\) を持つ。但し、\(\alpha<\beta\) とする。
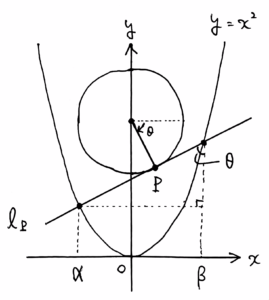
このとき、
\begin{align}
{L_{\rm P}}^2
&=\left\{\frac{1}{\sin\theta}\times(\beta-\alpha)\right\}^2\\
&=\frac{1}{\sin^2\theta}\times(\beta-\alpha)^2\\
&=\frac{1}{\sin^2\theta}\times\left\{(\alpha+\beta)^2-4\alpha\beta\right\}\\
&=\frac{1}{\sin^2\theta}\times\left\{\left(\frac{\cos\theta}{\sin\theta}\right)^2-4\frac{1-a\sin\theta}{\sin\theta}\right\}\\
&=\frac{1}{\sin^2\theta}\times\left(\frac{1}{\sin^2\theta}-\frac{4}{\sin\theta}+4a-1\right)
\end{align}
である。\(\displaystyle t=\frac{1}{\sin\theta}\) とおくと \(t\geq1\) であって
\begin{align}
{L_{\rm P}}^2
&=t^2\times\left(t^2-4t+4a-1\right)
\end{align}となる。よって、両辺を \(t\) で微分すると
\begin{gather}
2L_{\rm P}\frac{dL_{\rm P}}{dt}=2t\times\left(t^2-4t+4a-1\right)+t^2\times\left(2t-4\right)
\end{gather}
すなわち
\begin{gather}
L_{\rm P}\frac{dL_{\rm P}}{dt}=t\left\{2t^2-6t+(4a-1)\right\}
\end{gather}となる。
条件を満たすのは、\(t>1\) の範囲で \(\displaystyle \frac{dL_{\rm P}}{dt}\) の符号が変わるときである。今、\(L_{\rm P}>0\) かつ \(t>0\) なので、\(2t^2-6t+(4a-1)\) の符号が変われば良い。
そこで $$f(t)=2t^2-6t+(4a-1)$$ とおくと
\begin{gather}
f(t)=2\left(t-\frac{3}{2}\right)^2+4a-\frac{11}{2}
\end{gather}であって、\(\displaystyle\frac{3}{2}>1\) である。よって、\(f(t)\) は \(\displaystyle t=\frac{3}{2}\) のときに最小値 \(\displaystyle 4a-\frac{11}{2}\) をとる。これが負であれば良いので \(\displaystyle 4a-\frac{11}{2}<0\) すなわち \(\displaystyle a<\frac{11}{8}\) となる。
以上より、(1)の範囲と合わせて $$\frac{5}{4}<a<\frac{11}{8}$$ を得る。
考察と感想

(1)で円周 \(C\) をパラメータ(媒介変数)で表示したので、(2)でもそれを参考に接点 \({\rm P}\) を決めます。これによって、\(L_{\rm P}\) が \({\rm P}\) の関数であったのが、\(\theta\) の関数とも思えるようになります。これは、\({\rm P}\) と \(\theta\) が一対一に対応しているからできることで、図形的に解釈しやすい変数の取り方だと思います。
計算を進めると、\(L_{\rm P}\) を \(\theta\) によって表したときに \(\displaystyle \frac{1}{\sin\theta}\) が繰り返し現れます。考えている範囲で \(\theta\) と \(\displaystyle \frac{1}{\sin\theta}\) は一対一に対応するので、\(L_{\rm P}\) を \(\displaystyle t=\frac{1}{\sin\theta}\) の関数と見做すことができます。このとき、\({L_{\rm P}}^2\) が \(t\) の \(4\) 次関数であること、\(L_{\rm P}\) と \({L_{\rm P}}^2\) の増減が一致することから解析が進みます。
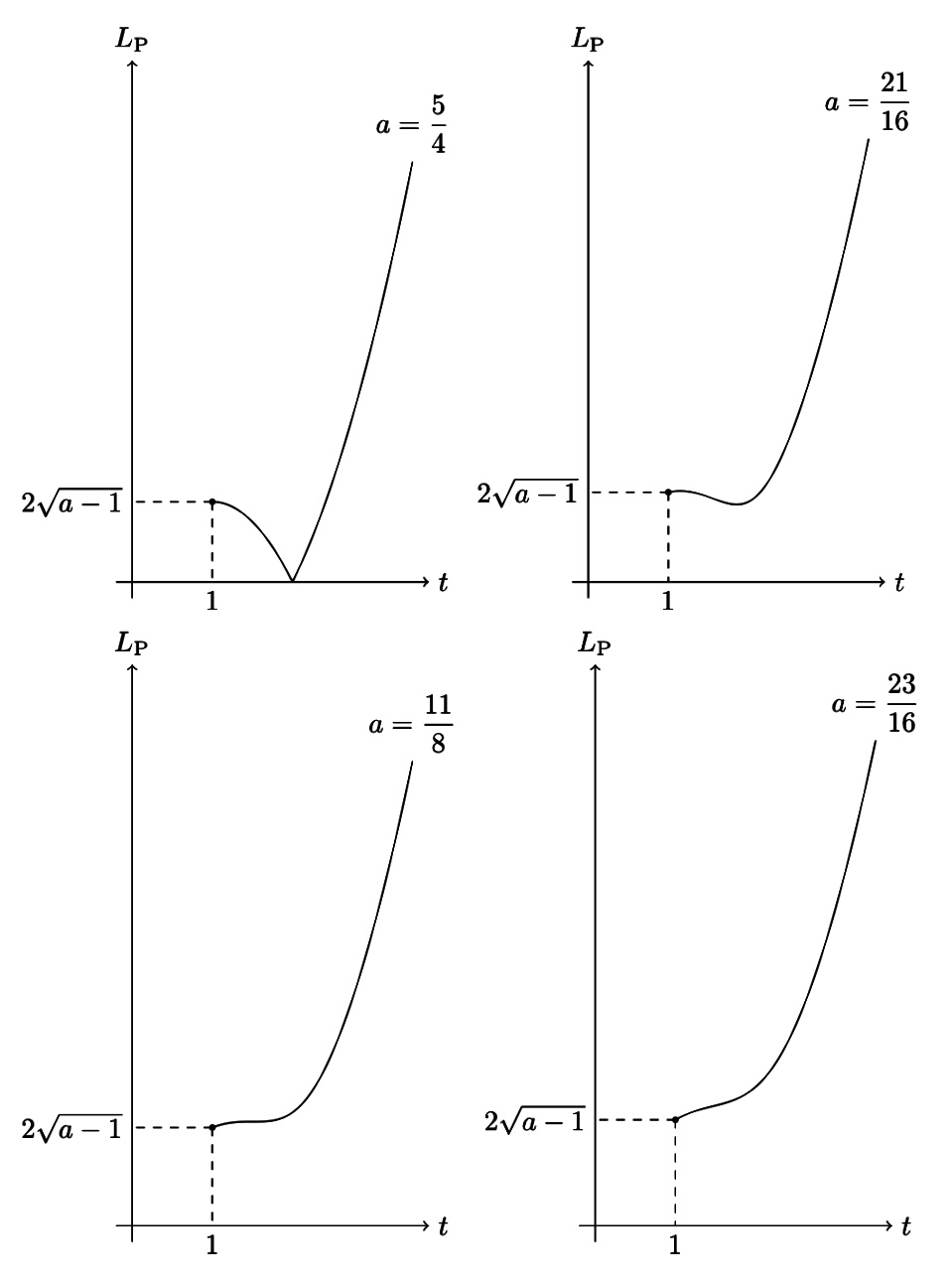
最後に、\(L_{\rm P}\) を \(t\) の関数としたときのグラフを、参考も含めて
- \(\displaystyle a=\frac{20}{16}=\frac{5}{4}\)
- \(\displaystyle a=\frac{21}{16}\)
- \(\displaystyle a=\frac{22}{16}=\frac{11}{8}\)
- \(\displaystyle a=\frac{23}{16}\)
の場合について描いておきます。


コメント