数学Bの「統計的な推測」の第1回として 確率変数と確率分布の基本 を扱います。(全7回)
今回は解説を含め、全5問を解いてゆきます。
確率変数の期待値
目の数字が \(1\),\(2\),\(3\),\(3\),\(5\),\(5\) であるさいころが \(1\) 個ある。このさいころを \(2\) 回投げ、出た目の積を \(4\) で割った余りを \(X\) とする。確率変数 \(X\) の期待値を求めよ。
解答例(その1)
縦軸と横軸にそれぞれ \(1\) 回目と \(2\) 回目に出た目をとり、その積を \(4\) で割った余りを書き込むと以下のようになる。
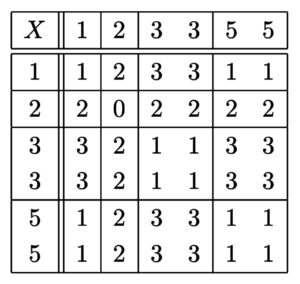
このとき、\(X\) のとり得る値 \(0\),\(1\),\(2\),\(3\) について(以下、その2と共通。)
- \(X=0\) となるの数は \(1\) 通り
- \(X=1\) となるの数は \(13\) 通り
- \(X=2\) となるの数は \(10\) 通り
- \(X=3\) となるの数は \(12\) 通り
よって、\(X\) の確率分布は以下の通り。
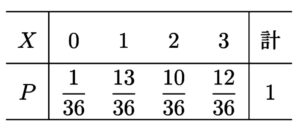
これより、\(X\) の期待値は
\begin{align}
E(X)
&=\frac{1}{36}\left(0\cdot1+1\cdot13+2\cdot10+3\cdot12\right)\\
&=\frac{69}{36}\\
&=\frac{23}{12}\quad(=1.91\dot{6})
\end{align}
解答例(その2)
合同式を知っていれば、目の数字は \(4\) を法として良いことがわかります。\(4\) で割るとき、余りについて \(1\) の目と \(5\) の目は同一視できます。このことから、以下のような解法も考えられます。
縦軸と横軸にそれぞれ \(1\) 回目と \(2\) 回目に出た目を \(4\) を法としてとり、その積を \(4\) で割った余りを書き込むと以下のようになる。
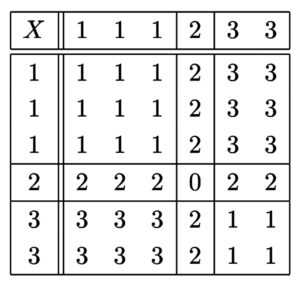
このとき、\(X\) のとり得る値 \(0\),\(1\),\(2\),\(3\) について…(以下、その1と同様。)
分散と標準偏差
白球 \(2\) 個と黒球 \(4\) 個が入った袋から \(1\) 個ずつ球を取り出すことを繰り返す。但し、取り出した球は袋に戻さないものとする。\(2\) 個目の白球が取り出されたとき、その時点で取り出した球の総数を \(X\) とする。確率変数 \(X\) の期待値、分散、標準偏差を求めよ。
解答例(その1)
\(X\) のとり得る値は \(2\),\(3\),\(4\),\(5\),\(6\) である。
- \(X=2\) となるのは「白白」のときで
\begin{align}
P(X=2)
&=\frac{2}{6}\cdot\frac{1}{5}
=\frac{1}{15}
\end{align} - \(X=3\) となるのは「黒白白」または「白黒白」のときで
\begin{align}
P(X=3)
&=\frac{4}{6}\cdot\frac{2}{5}\cdot\frac{1}{4}+\frac{2}{6}\cdot\frac{4}{5}\cdot\frac{1}{4}\\
&=\frac{2}{15}
\end{align} - \(X=4\) となるのは「黒黒白白」,「黒白黒白」,「白黒黒白」のときで
\begin{align}
P(X=4)
&=\frac{4}{6}\cdot\frac{3}{5}\cdot\frac{2}{4}\cdot\frac{1}{3}\\
&\qquad+\frac{4}{6}\cdot\frac{2}{5}\cdot\frac{3}{4}\cdot\frac{1}{3}\\
&\qquad+\frac{2}{6}\cdot\frac{4}{5}\cdot\frac{3}{4}\cdot\frac{1}{3}\\
&=\frac{3}{15}
\end{align} - \(X=5\) となるのは「黒黒黒白白」,「黒黒白黒白」,「黒白黒黒白」,「白黒黒黒白」のときで
\begin{align}
P(X=5)
&=\frac{4}{6}\cdot\frac{3}{5}\cdot\frac{2}{4}\cdot\frac{2}{3}\cdot\frac{1}{2}\\
&\qquad+\frac{4}{6}\cdot\frac{3}{5}\cdot\frac{2}{4}\cdot\frac{2}{3}\cdot\frac{1}{2}\\ &\qquad+\frac{4}{6}\cdot\frac{2}{5}\cdot\frac{3}{4}\cdot\frac{2}{3}\cdot\frac{1}{2}\\ &\qquad+\frac{2}{6}\cdot\frac{4}{5}\cdot\frac{3}{4}\cdot\frac{2}{3}\cdot\frac{1}{2}\\ &=\frac{4}{15}
\end{align} - \(X=6\) となるのは上記の場合以外なので
\begin{align}
P(X=6)
&=1-\left(\frac{1}{15}+\frac{2}{15}+\frac{3}{15}+\frac{4}{15}\right)\\
&=1-\frac{10}{15}\\
&=\frac{5}{15}
\end{align}
よって、期待値は
\begin{align}
E(X)
&=\frac{1}{15}\left(2\cdot1+3\cdot2+4\cdot3+5\cdot4+6\cdot5\right)\\
&=\frac{70}{15}\\
&=\frac{14}{3}\quad(=4.\dot{6})
\end{align}
また、
\begin{align}
E(X^2)
&=\frac{1}{15}\left(2^2\cdot1+3^2\cdot2+4^2\cdot3+5^2\cdot4+6^2\cdot5\right)\\
&=\frac{350}{15}\\
&=\frac{70}{3}
\end{align}
より、分散は(以下、その2と共通。)
\begin{align}
V(X)
&=E(X^2)-E(X)^2\\
&=\frac{70}{3}-\left(\frac{14}{3}\right)^2\\
&=\frac{14}{9}
\end{align}
さらに、標準偏差は
\begin{align}
\sigma(X)
=\sqrt{\frac{14}{9}}
=\frac{\sqrt{14}}{3}\quad(≒1.247)
\end{align}
解答例(その2)
\(6\) 個すべての球を取り出す場合を考えても良いです。一般の確率 \(P(X=k)\) を求めることで、期待値や分散を求めるときに数列の和 \(\sum\) の公式を使うことができます。
\(X\) のとり得る値は \(2\),\(3\),\(4\),\(5\),\(6\) である。球を取り出した順に左から一列に並べ、\(6\) 個すべて並べたとし、\(X=k\)(\(k=2,3,4,5,6\))のときを考える。
- \(k\) 番目は白球が \({}_2{\rm C}_1=2\) 通りで並ぶ。
- 残った白球は \(1,2,\ldots,k-1\) 番目のうちの \(1\) 箇所に並ぶので \(k-1\) 通り。
- 黒球は残る \(4\) 箇所に並ぶので \(4!\) 通り。
これより、
\begin{align}
P(X=k)
=\frac{2\times(k-1)\times4!}{6!}=\frac{k-1}{15}
\end{align}
よって、期待値は
\begin{align}
E(X)
&=\sum_{k=2}^6 \left(k\times\frac{k-1}{15}\right)\\
&=\frac{1}{15}\sum_{k=1}^6 \left(k^2-k\right)\\
&=\frac{1}{15}\left(\frac{6\cdot7\cdot13}{6}-\frac{6\cdot7}{2}\right)\\
&=\frac{70}{15}\\
&=\frac{14}{3}\quad(=4.\dot{6})
\end{align}
また、
\begin{align}
E(X^2)
&=\sum_{k=2}^6 \left(k^2\times\frac{k-1}{15}\right)\\
&=\frac{1}{15}\sum_{k=1}^6 \left(k^3-k^2\right)\\
&=\frac{1}{15}\left(\frac{6^2\cdot7^2}{4}-\frac{6\cdot7\cdot13}{6}\right)\\
&=\frac{70}{3}
\end{align}
より、分散は…(以下、その1と同様。)
数列の和の応用
黒石が \(2\) 個、白石が \(n\) 個ある。これらを無作為に \(1\) 個ずつ一列に並べてゆく。このとき、\(2\) 個の黒石の間にある白石の個数を \(X\) とする。確率変数 \(X\) の期待値と分散を求めよ。
解答例
\(X\) のとり得る値は \(0,1,\ldots,n\) である。\(k=0,1,\ldots,n\) に対して \(X=k\) とすると、黒石の間にない白石は \(n-k\) 個である。黒石とその間にある白石は、間にない \(n-k\) 個の白石の間か両端の \(n-k+1\) 箇所のいずれか \(1\) 箇所にある。各々の黒色と色の配置に対して、石は \(n!\times2!\) 通りの並べ方があるので
\begin{align}
P(X=k)
&=\frac{(n-k+1)\times(n!\times2!)}{(n+2)!}\\
&=\frac{2(n-k+1)}{(n+1)(n+2)}
\end{align}
よって、期待値は
\begin{align}
E(X)
&=\sum_{k=0}^n \left\{k\times\frac{2(n-k+1)}{(n+1)(n+2)}\right\}\\
&=\frac{2}{(n+1)(n+2)}\sum_{k=1}^n \{(n+1)k-k^2\}\\
&=\frac{2}{(n+1)(n+2)}\left\{\frac{1}{2}n(n+1)^2-\frac{1}{6}n(n+1)(2n+1)\right\}\\
&=\frac{n}{3(n+2)}\left\{3(n+1)-(2n+1)\right\}\\
&=\frac{n}{3}
\end{align}
また、
\begin{align}
E(X^2)
&=\sum_{k=0}^n \left\{k^2\times\frac{2(n-k+1)}{(n+1)(n+2)}\right\}\\
&=\frac{2}{(n+1)(n+2)}\sum_{k=1}^n \{(n+1)k^2-k^3\}\\
&=\frac{2}{(n+1)(n+2)}\left\{\frac{1}{6}n(n+1)^2(2n+1)-\frac{1}{4}n^2(n+1)^2\right\}\\
&=\frac{n(n+1)}{6(n+2)}\left\{2(2n+1)-3n\right\}\\
&=\frac{n(n+1)}{6}
\end{align}
であるので、分散は
\begin{align}
V(X)
&=E(X^2)-E(X)^2\\
&=\frac{n(n+1)}{6}-\left(\frac{n}{3}\right)^2\\
&=\frac{n(n+1)}{6}-\frac{n^2}{9}\\
&=\frac{n\{3(n+1)-2n\}}{18}\\
&=\frac{n(n+3)}{18}
\end{align}
確率変数の変換
\(1\) ではない定数 \(a\) に対し、確率変数 \(X\) のとり得る値が \(\{1,a\}\) であるとする。確率変数 \(Y=3X-1\) の期待値と分散がそれぞれ \(5\) と \(9\) であるとき、\(a\) の値を求めよ。
解答例
\(P(X=1)=p\)(\(0\leq p\leq1\))とおくと、\(P(X=a)=1-p\) である。
このとき、
\begin{align}
E(X)
&=1\cdot p+a\cdot(1-p)\\
&=(1-a)p+a
\end{align}
であるので、\(5=E(Y)=3E(X)-1\) すなわち \(E(X)=2\) より
\begin{align}
(1-a)p+a=2\tag{1}
\end{align}
である。
一方、
\begin{align}
V(X)
&=1^2\cdot p+a^2\cdot(1-p)-E(X)^2\\
&=(1-a^2)p+a^2-4
\end{align}
であるので、\(9=V(Y)=9V(X)\) すなわち \(V(X)=1\) より
\begin{align}
(1-a^2)p+a^2=5\tag{2}
\end{align}
である。
よって、式 (1) より \((1-a)p=2-a\) なので、式 (2) より
\begin{align}
(1+a)(1-a)p+a^2&=5\\
(1+a)(2-a)+a^2&=5\\
2+a&=5\\
a&=3
\end{align}
を得る。このとき、式 (1) より \(p=\dfrac{1}{2}\) なので \(0\leq p\leq1\) を満たす。
以上より、\(a=3\) である。
\(2\) 変数の同時分布
\(1\),\(2\),\(3\) の数字を書いたカードが、それぞれ \(2\) 枚,\(3\) 枚,\(5\) 枚の計 \(10\) 枚ある。これらのカードを元に戻さず、無作為に \(1\) 枚ずつ \(2\) 回選び出す。\(1\) 回目に選んだカードの数字を \(X\) とし、\(2\) 回目に選んだカードの数字を \(Y\) とするとき、\(X\) と \(Y\) の同時分布を求めよ。
解答例
\(X\) と \(Y\) のとり得る値は共に \(1,2,3\) であって
\begin{align}
P(X=1, Y=1)&=\frac{2}{10}\cdot\frac{1}{9}=\frac{2}{90}\\
P(X=1, Y=2)&=\frac{2}{10}\cdot\frac{3}{9}=\frac{6}{90}\\
P(X=1, Y=3)&=\frac{2}{10}\cdot\frac{5}{9}=\frac{10}{90}\\ \\
P(X=2, Y=1)&=\frac{3}{10}\cdot\frac{2}{9}=\frac{6}{90}\\
P(X=2, Y=2)&=\frac{3}{10}\cdot\frac{2}{9}=\frac{6}{90}\\
P(X=2, Y=3)&=\frac{3}{10}\cdot\frac{5}{9}=\frac{15}{90}\\ \\
P(X=3, Y=1)&=\frac{5}{10}\cdot\frac{2}{9}=\frac{10}{90}\\
P(X=3, Y=2)&=\frac{5}{10}\cdot\frac{3}{9}=\frac{15}{90}\\
P(X=3, Y=3)&=\frac{5}{10}\cdot\frac{4}{9}=\frac{20}{90}
\end{align}
よって、\(X\) と \(Y\) の同時分布は以下の通り。
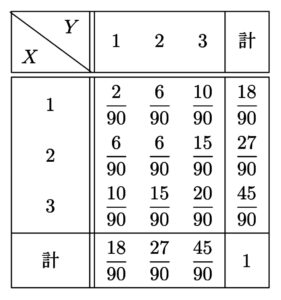
最後に。
分散 \(V(X)\) を求める際、今回は $$V(X)=E(X^2)-E(X)^2$$ という公式を用いました。定義通りにいけば $$V(X)=E((X-m)^2)$$ ですので、もちろんそれでも構いません。ただ、偏差 \(X-m\) が整数でないと計算が複雑になってしまうので、前者の公式を採用しました。偏差が整数の場合は後者の定義の方が楽な場合もあります。
お疲れ様でした。


コメント