座標空間内の \(4\) 点 \({\rm O}(0,0,0)\),\({\rm A}(2,0,0)\),\({\rm B}(1,1,1)\),\({\rm C}(1,2,3)\) を考える。
(1)\(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OA}\),\(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OB}\),\(\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OC}=1\) を満たす点 \({\rm P}\) の座標を求めよ。
(2)点 \({\rm P}\) から直線 \({\rm AB}\) に垂線を下ろし、その垂線と直線 \({\rm AB}\) の交点を \({\rm H}\) とする。\(\overrightarrow{\rm OH}\) を \(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) を用いて表せ。
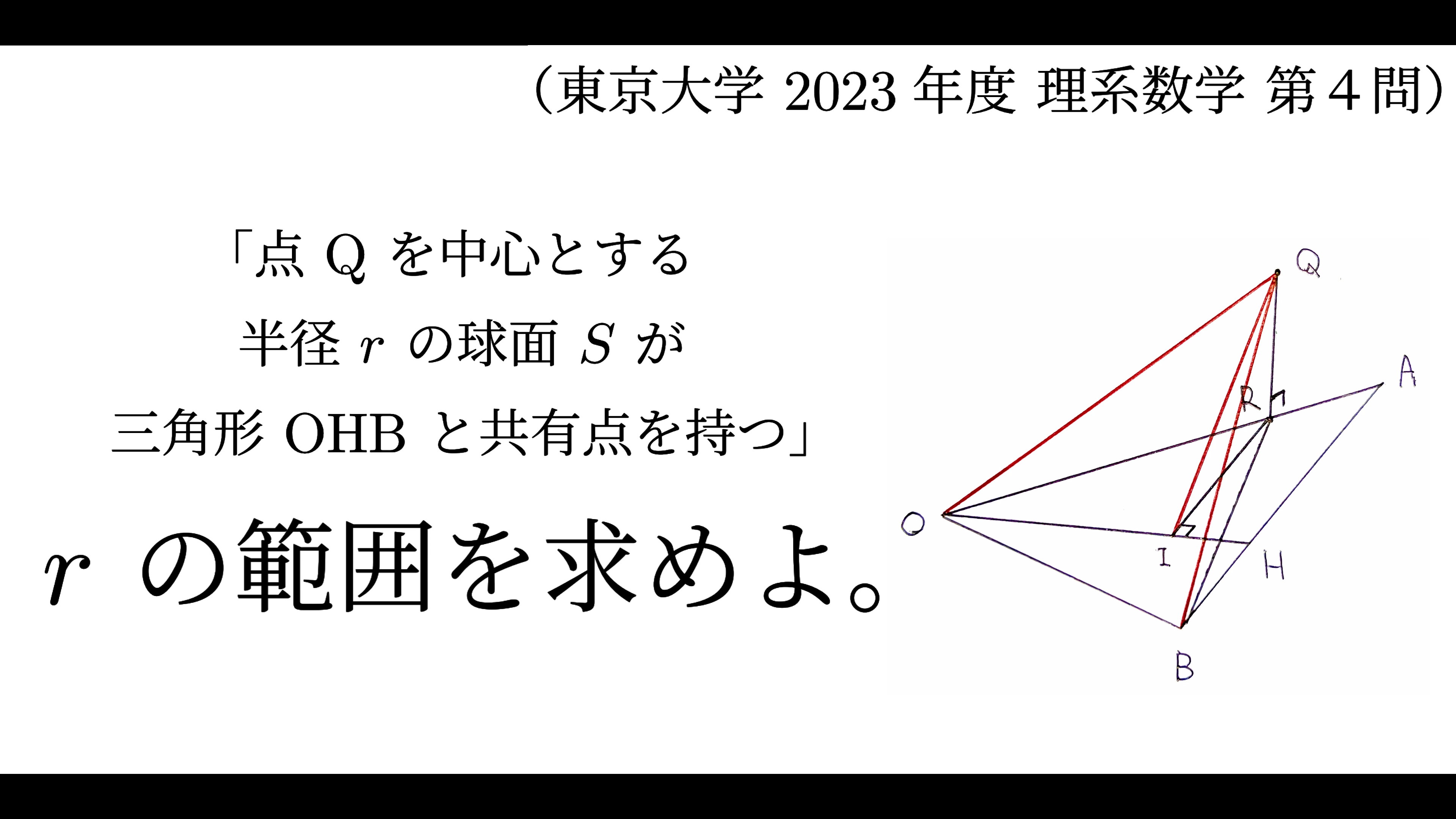
(3)点 \({\rm Q}\) を \(\displaystyle \overrightarrow{\rm OQ}=\frac{3}{4}\overrightarrow{\rm OA}+\overrightarrow{\rm OP}\) により定め、\({\rm Q}\) を中心とする半径 \(r\) の球面 \(S\) を考える。\(S\) が三角形 \({\rm OHB}\) と共有点を持つような \(r\) の範囲を求めよ。ただし、三角形 \({\rm OHB}\) は \(3\) 点 \({\rm O}\),\({\rm H}\),\({\rm B}\) を含む平面内にあり、周とその内部からなるものとする。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
【解答例】

(1)
\({\rm P}(u,v,w)\) とおく。このとき、
- \(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OA}\) より
\begin{align}
\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OA}
=\left(\begin{array}{c}u\\v\\w\end{array}\right)\cdot\left(\begin{array}{c}2\\0\\0\end{array}\right)
=0
\end{align}であるので \(u=0\) を得る。 - \(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OB}\) より
\begin{align}
\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OB}
=\left(\begin{array}{c}0\\v\\w\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\1\end{array}\right)
=0
\end{align}であるので \(v=-w\) を得る。 - \(\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OC}=1\) より
\begin{align}
\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OC}
=\left(\begin{array}{c}0\\-w\\w\end{array}\right)\cdot\left(\begin{array}{c}1\\2\\3\end{array}\right)
=1
\end{align}であるので \(w=1\) を得る。
よって、\({\rm P}(0,-1,1)\) である。
(2)
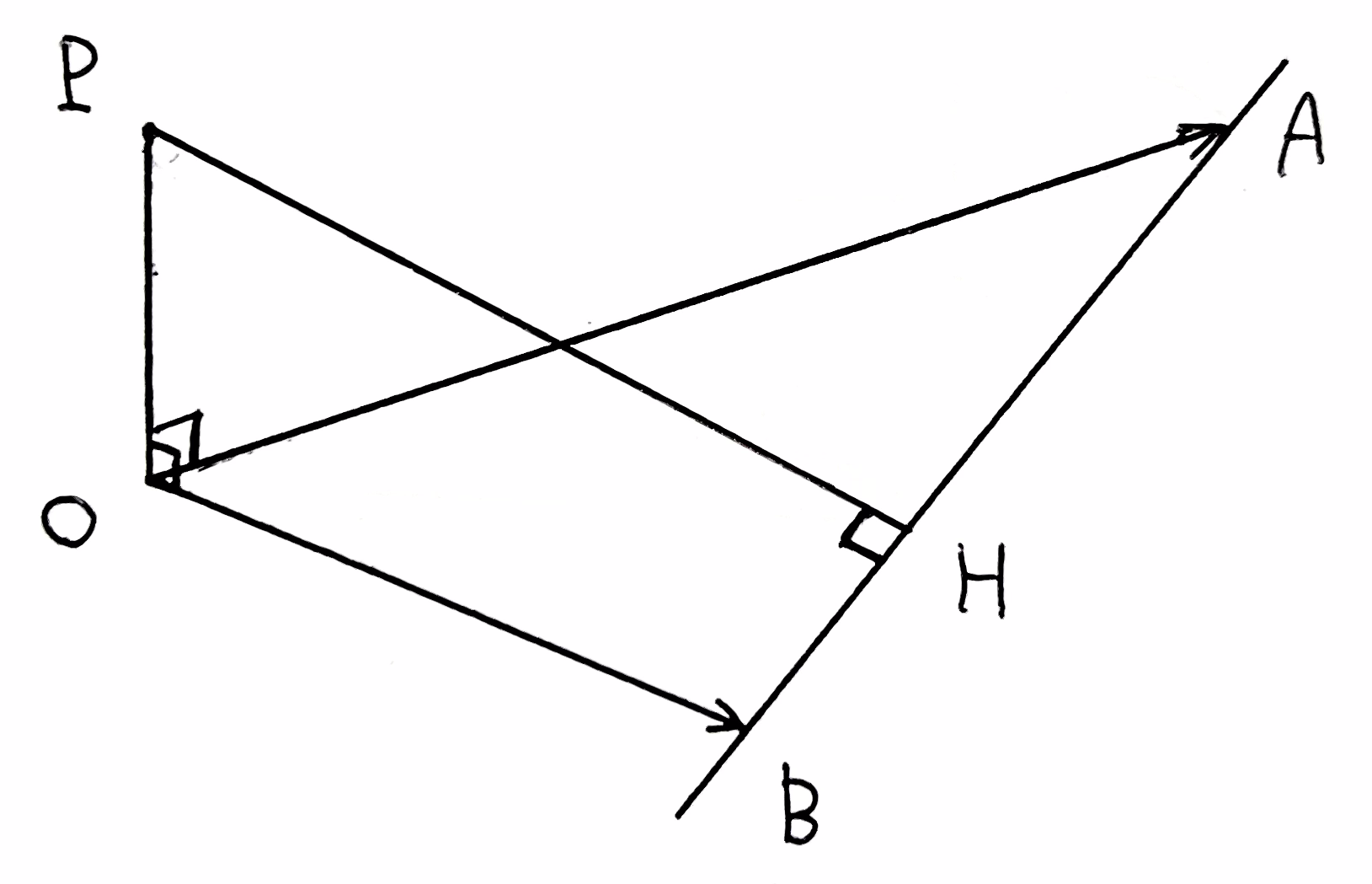
点 \({\rm H}\) は直線 \({\rm AB}\) 上の点であるので、実数 \(t\) を用いて
\begin{align}
\overrightarrow{\rm OH}
&=(1-t)\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}\\
&=(1-t)\left(\begin{array}{c}2\\0\\0\end{array}\right)+t\left(\begin{array}{c}1\\1\\1\end{array}\right)\\
&=\left(\begin{array}{c}2-t\\t\\t\end{array}\right)
\end{align}と書ける。よって、\(\overrightarrow{\rm PH}\perp\overrightarrow{\rm AB}\) より
\begin{align}
\overrightarrow{\rm PH}\cdot\overrightarrow{\rm AB}
=\left(\begin{array}{c}2-t\\t+1\\t-1\end{array}\right)\cdot\left(\begin{array}{c}-1\\1\\1\end{array}\right)
=0
\end{align}すなわち $$(t-2)+(t+1)+(t-1)=0$$ であるので \(\displaystyle t=\frac{2}{3}\) を得る。これより、
\begin{align}
\overrightarrow{\rm OH}
&=\frac{1}{3}\overrightarrow{\rm OA}+\frac{2}{3}\overrightarrow{\rm OB}
\end{align}である。
(3)
まず、
\begin{align}
\overrightarrow{\rm PQ}
=\overrightarrow{\rm OQ}-\overrightarrow{\rm OP}
=\frac{3}{4}\overrightarrow{\rm OA}
\end{align}であるので、線分 \({\rm OA}\) を \(3:1\) に内分する点を \({\rm R}\) とすると \(\displaystyle \frac{3}{4}\overrightarrow{\rm OA}=\overrightarrow{\rm OR}\) なので
\begin{align}
\overrightarrow{\rm OQ}-\overrightarrow{\rm OP}=\overrightarrow{\rm OR}
\end{align}すなわち
\begin{align}
\overrightarrow{\rm RQ}=\overrightarrow{\rm OP}
\end{align}である。よって、直線 \({\rm RQ}\) は \(3\) 点 \({\rm O}\),\({\rm A}\),\({\rm B}\) が定める平面 \(\alpha\) に直交する。また、
\begin{align}
{\rm RQ}={\rm OP}=\sqrt{2}
\end{align}である。
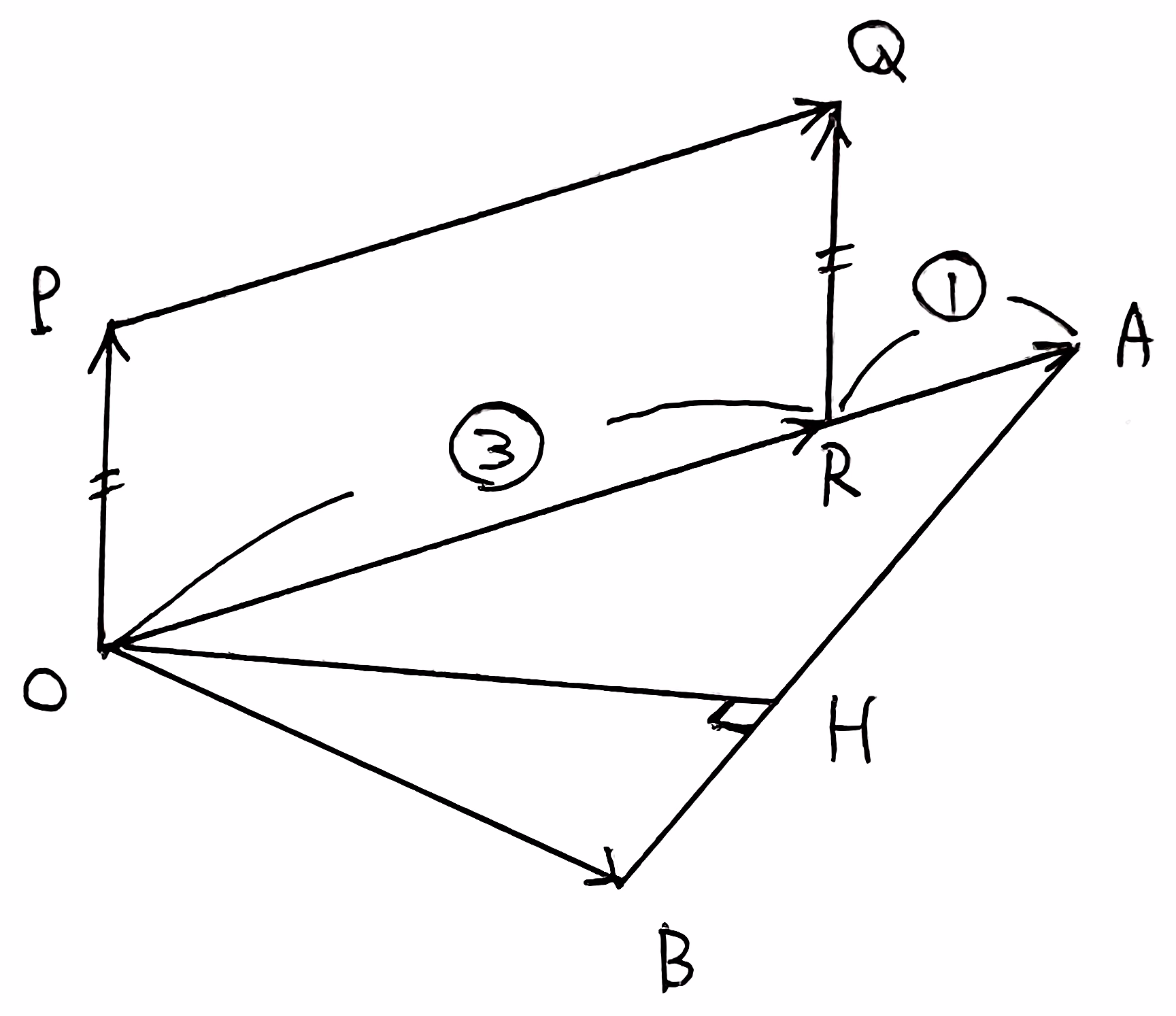
次に、\(\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}=0\) かつ \(\overrightarrow{\rm PH}\cdot\overrightarrow{\rm AB}=0\) であるので、\(\displaystyle \overrightarrow{\rm OH}=\overrightarrow{\rm OP}+\overrightarrow{\rm PH}\) より
\begin{align}
\overrightarrow{\rm OH}\cdot\overrightarrow{\rm AB}=0+0=0
\end{align}すなわち \(\overrightarrow{\rm OH}\perp\overrightarrow{\rm AB}\) である。また、(2)より \(\displaystyle \overrightarrow{\rm OH}=\frac{2}{3}\left(\begin{array}{c}2\\1\\1\end{array}\right)\) である。
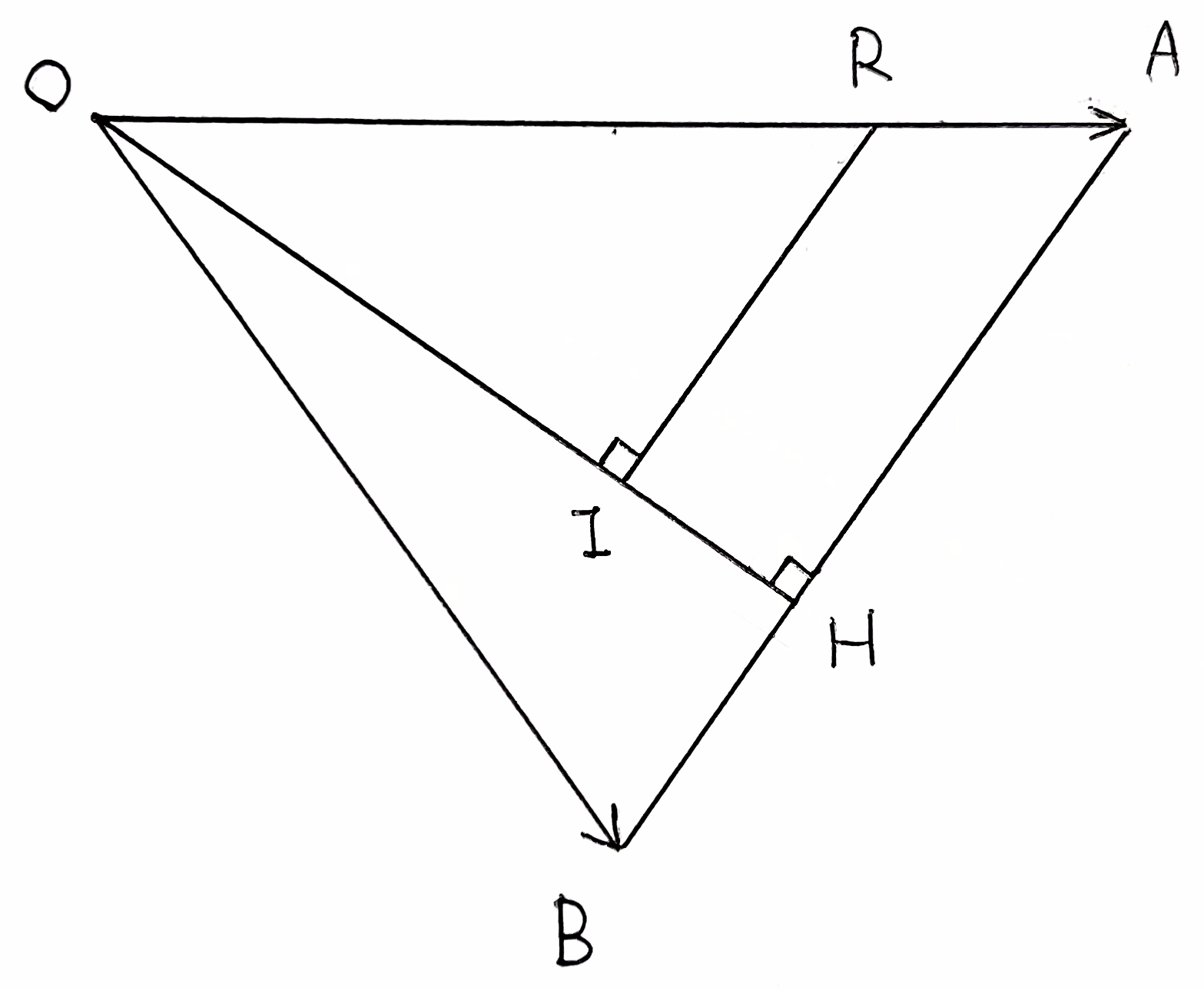
- 点 \({\rm R}\) から直線 \({\rm OH}\) に下ろした垂線の足を \({\rm I}\) とすると \(\triangle{\rm OAH}\sim\triangle{\rm ORI}\) より
\begin{align}
{\rm RI}^2
&=\left(\frac{3}{4}\right)^2\times{\rm AH}^2\\
&=\frac{9}{16}\times\left({\rm OA}^2-{\rm OH}^2\right)\\
&=\frac{9}{16}\times\left(4-\frac{24}{9}\right)\\
&=\frac{3}{4}
\end{align} - 同じく \(\triangle{\rm OAH}\sim\triangle{\rm ORI}\) より
\begin{align}
{\rm RO}^2
&=\left(\frac{3}{4}\right)^2\times{\rm AO}^2\\
&=\frac{3}{16}\times4\\
&=\frac{9}{4}
\end{align} - \(\displaystyle \overrightarrow{\rm RB}=\frac{1}{2}\left(\begin{array}{c}-1\\2\\2\end{array}\right)\) であるので $${\rm RB}^2=\left(\frac{1}{2}\right)^2\times9=\frac{9}{4}$$
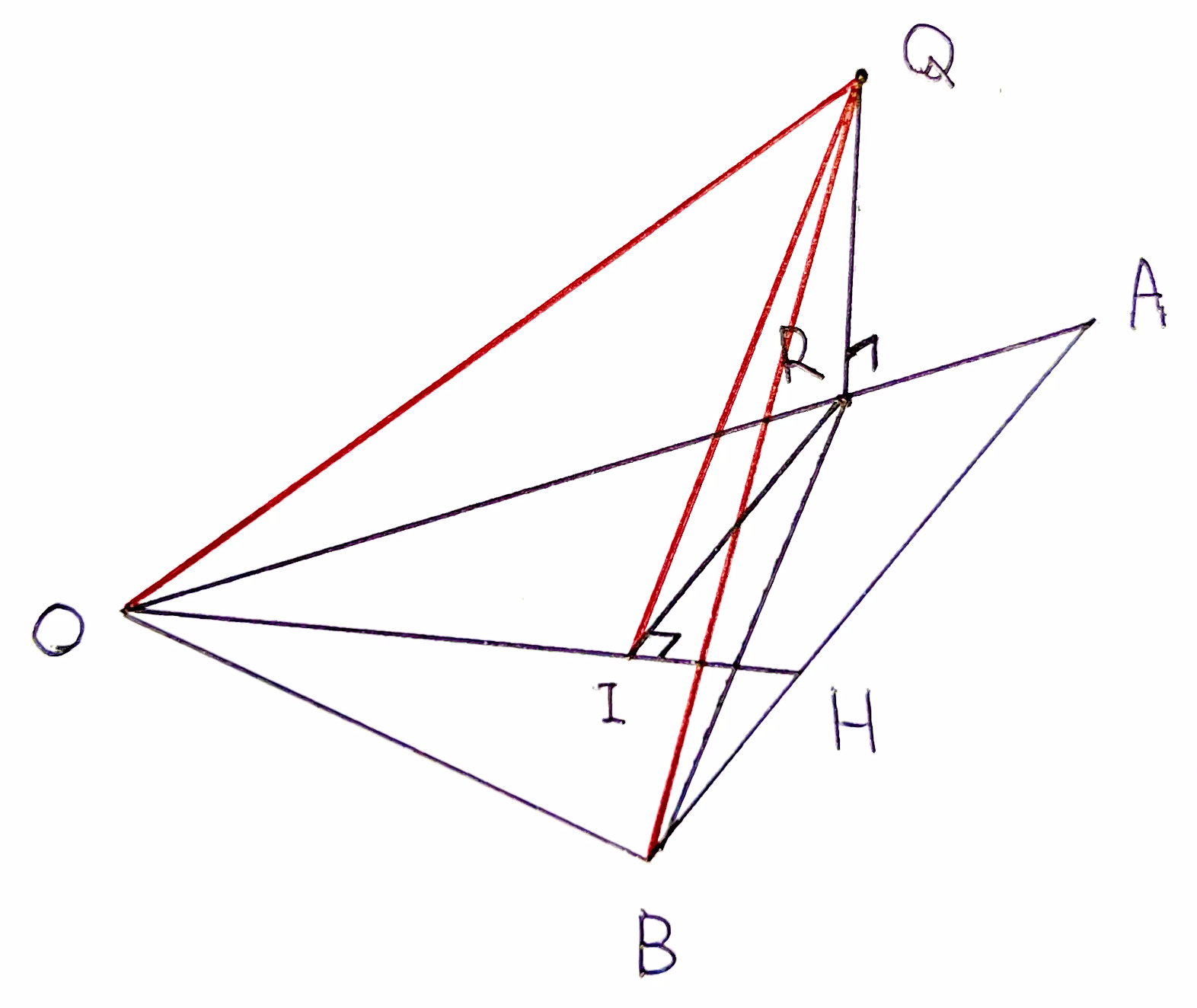
ここで、平面 \(\alpha\) 上にある \(\triangle{\rm OHB}\) 上の点 \({\rm X}\) に対して、常に $$\overrightarrow{\rm QR}\perp\overrightarrow{\rm RX}$$ である。よって、$$r^2={\rm QR}^2+{\rm RX}^2$$ と書ける。
今、\({\rm QR}^2=2\) で一定なので \({\rm RX}^2\) のとり得る値の範囲を考えれば良い。1. 2. 3. より$$\frac{3}{4}\leq{\rm RX}^2\leq\frac{9}{4}$$ すなわち $$\frac{11}{4}\leq r^2\leq\frac{17}{4}$$ である。よって、\(r>0\) より $$\frac{\sqrt{11}}{2}\leq r\leq\frac{\sqrt{17}}{2}$$ を得る。
考察と感想

(1)について
条件 \(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OA}\),\(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OB}\) から、直線 \({\rm OP}\) は \(3\) 点 \({\rm O}\),\({\rm A}\),\({\rm B}\) が定める平面 \(\alpha\) と垂直な関係にあることがわかります。
各点には座標が与えられていますが、それは計算のときに用いるものとして、例えば平面 \(\alpha\) を水平にしたように見える視点だと状況を把握しやすいと思います。
点 \({\rm P}\) が、点 \({\rm O}\) を通り平面 \(\alpha\) に垂直な直線上のどの位置にあるかを、条件 \(\overrightarrow{\rm OP}\cdot\overrightarrow{\rm OC}=1\) によって決定しています。
(2)について
点 \({\rm H}\) は直線 \({\rm AB}\) 上にあるので、ひとつの文字 \(t\) を用いて、\(\overrightarrow{\rm OH}\) を \(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) の 線型結合 として表すことができます。そこで、\(\overrightarrow{\rm PH}\perp\overrightarrow{\rm AB}\) より、内積を考えて具体的な \(t\) の値を決定します。
(3)について
点 \({\rm Q}\) は線分 \({\rm OA}\) 上の点 \({\rm R}\) の真上にあります。半径 \(r\) について、点 \({\rm Q}\) と平面 \(\alpha\) との距離は \({\rm QR}=\sqrt{2}\) で一定です。よって、平面 \(\alpha\) において、\(\triangle{\rm OHB}\) 上の点 \({\rm X}\) と点 \({\rm R}\) との距離を考えれば良いことになります。


コメント