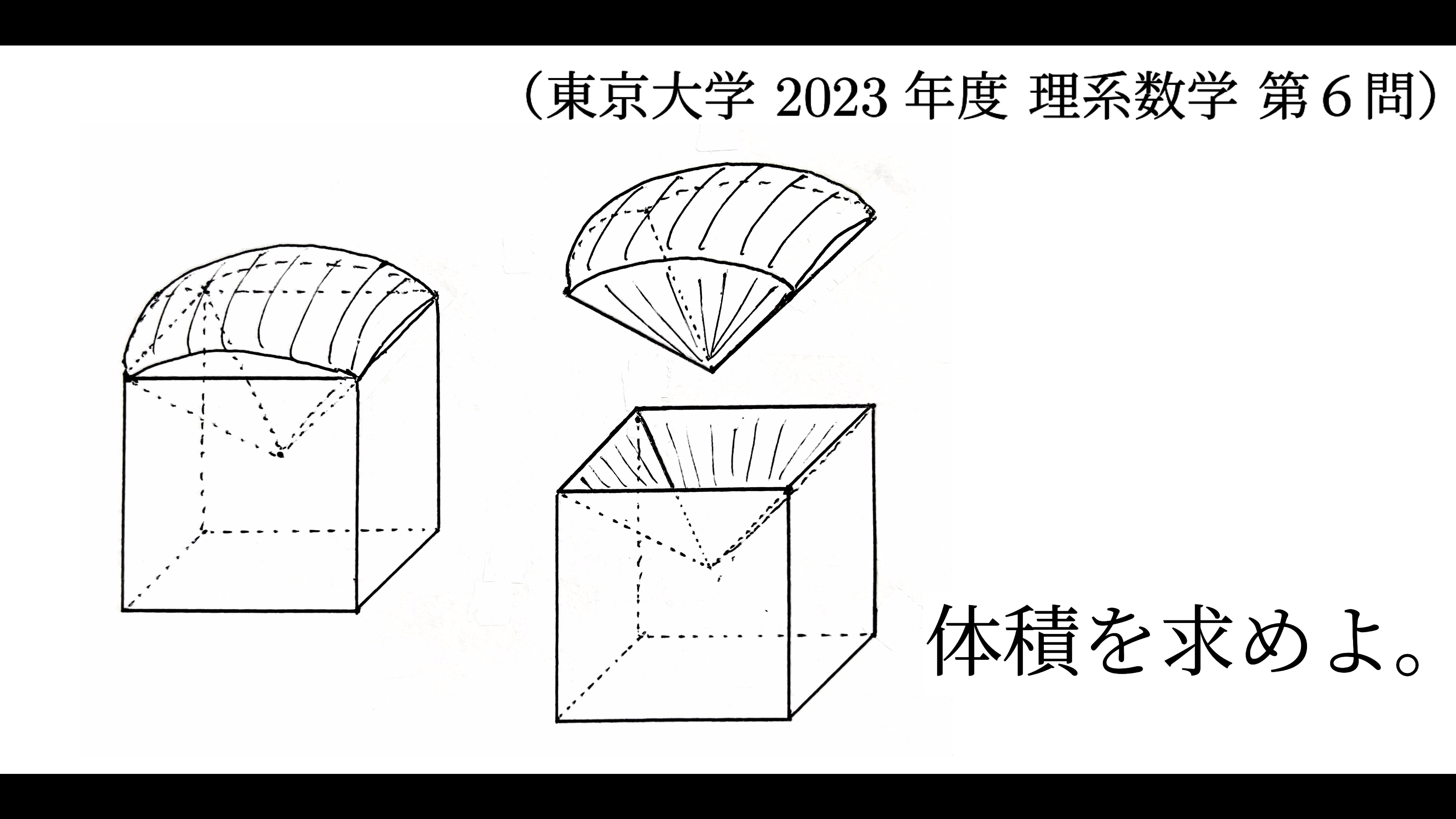
\({\rm O}\) を原点とする座標空間において、不等式 \(|x|\leq1\),\(|y|\leq1\),\(|z|\leq1\) の表す立方体を考える。その立方体の表面のうち、\(z<1\) を満たす部分を \(S\) とする
以下、座標空間内の \(2\) 点 \({\rm A}\),\({\rm B}\) が一致するとき、線分 \({\rm AB}\) は点 \({\rm A}\) を表すものとし、その長さを \(0\) と定める。
(1)座標空間内の点 \({\rm P}\) が次の条件(i),(ii)をともに満たすとき,点 \({\rm P}\) が動きうる範囲 \(V\) の体積を求めよ.
(i)\({\rm OP}\leq\sqrt{3}\)
(ii)線分 \({\rm OP}\) と \(S\) は、共有点を持たないか、点 \({\rm P}\) のみを共有点に持つ。
(2)座標空間内の点 \({\rm N}\) と点 \({\rm P}\) が次の条件(iii),(iv),(v)をすべて満たすとき、点 \({\rm P}\) が動きうる範囲 \(W\) の体積を求めよ。必要ならば、$$\sin\alpha=\frac{1}{\sqrt{3}}$$ を満たす実数 \(\alpha\) \(\displaystyle \left(0<\alpha<\frac{\pi}{2}\right)\) を用いてよい。
(iii)\({\rm ON}+{\rm NP}\leq\sqrt{3}\)
(iv)線分 \({\rm ON}\) と \(S\) は共有点を持たない。
(v)線分 \({\rm NP}\) と \(S\) は、共有点を持たないか、点 \({\rm P}\) のみを共有点に持つ。
本記事を含む 大学入試カテゴリー もあります。何か参考になれば幸いです。
解答例

(1)
条件(i)より、点 \({\rm P}\) は立方体の全ての頂点を通り原点を中心とする球面、及び、その内部に存在する。
条件(ii)より、点 \({\rm P}\) が立方体の外部に出るのは線分 \({\rm OP}\) が立方体の表面のうち \(z=1\) なる面と点 \({\rm P}\) 以外で共有点を持つときのみである。
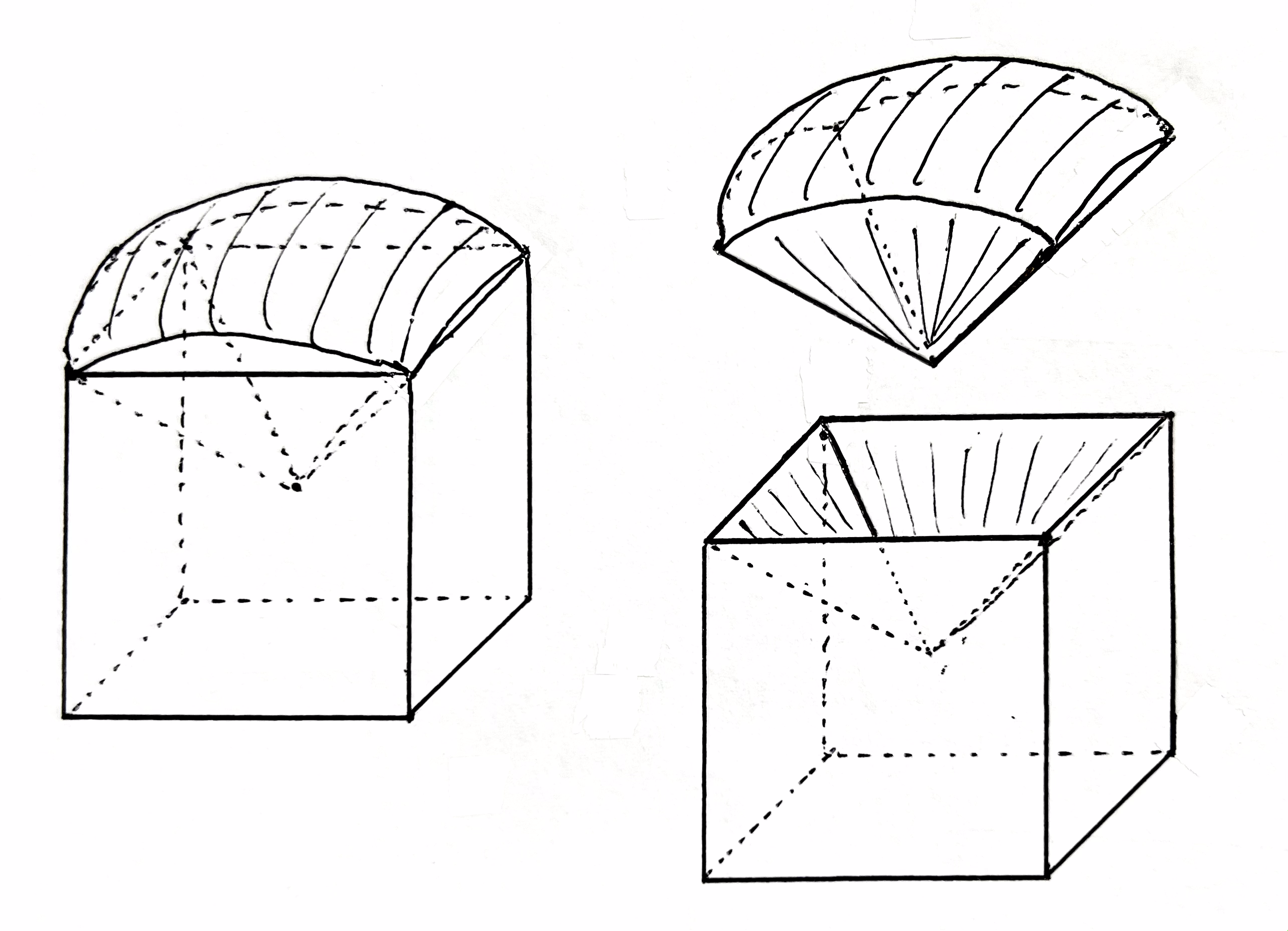
立方体の \(6\) 面についての対称性より、\(V\) の体積は
\begin{align}
&\frac{4\pi}{3}\times\left(\sqrt{3}\right)^3\times\frac{1}{6}+2^3\times\frac{5}{6}\\
&\quad=\frac{2\sqrt{3}}{3}\pi+\frac{20}{3}
\end{align}である。
(2)
(1)に対して、線分 \({\rm OP}\) が途中の点 \({\rm N}\) で折れ曲がることを許すので、点 \({\rm P}\) の存在し得る範囲は広がる。
立方体の \(2\) 頂点 \({\rm X}(1,1,1)\),\({\rm Y}(1,-1,1)\) と原点 \({\rm O}\) を通る平面を \(\beta\) とおく。このとき、\(V\) と \(\beta\) の共有部分で、立方体の外部にある部分 \(U\) を考え、その回転体の体積を求める。
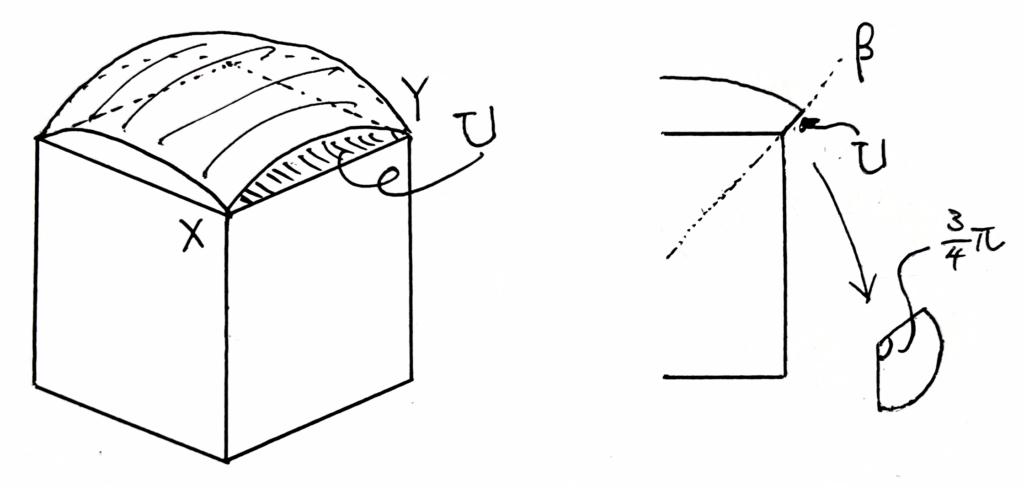
平面 \(\beta\) 上で原点を中心とする半径 \(\sqrt{3}\) の円を考え、点 \({\rm P}\) がその円周上にあるときを考える。
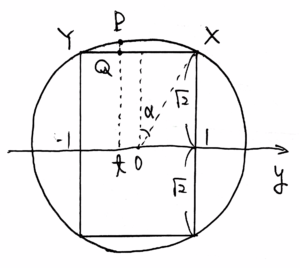
点 \({\rm P}\) の \(y\) 座標を \(t\) とすると \(-1\leq t\leq1\) である。また、点 \({\rm P}\) から辺 \({\rm XY}\) に下ろした垂線の足を \({\rm Q}\) とおく。このとき、
\begin{align}
{\rm PQ}=\sqrt{3-t^2}-\sqrt{2}
\end{align}であるので
\begin{align}
{\rm PQ}^2
&=(3-t^2)-2\sqrt{2}\sqrt{3-t^2}+2\\
&=5-2\sqrt{2}\sqrt{3-t^2}-t^2
\end{align}である。
ここで、平面 \(\beta\) と立方体の表面のうち \(x=1\) なる面①のなす角は \(2\pi\) の \(\displaystyle \frac{3}{8}\) である。
よって、\(U\) の回転体と同じ立体を \(4\) 箇所で考えるので、\(W\) から \(V\) を除いた部分の体積は
\begin{align}
&\pi\int_{-1}^1\left(5-2\sqrt{2}\sqrt{3-t^2}-t^2\right)dt\times\frac{3}{8}\times4\\
&\quad=3\pi\int_0^1\left(5-2\sqrt{2}\sqrt{3-t^2}-t^2\right)dt\\
&\quad=3\pi\left(5-2\sqrt{2}\int_0^1\sqrt{3-t^2}dt-\frac{1}{3}\right)\\
&\quad=\left(14-6\sqrt{2}\int_0^1\sqrt{3-t^2}dt\right)\pi
\end{align}
となる。
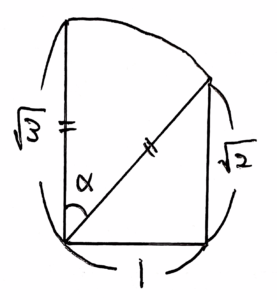
今、
\begin{align}
\int_0^1\sqrt{3-t^2}dt
&=\frac{\alpha}{2}\times\left(\sqrt{3}\right)^2+1\times\sqrt{2}\times\frac{1}{2}\\
&=\frac{3}{2}\alpha+\frac{1}{\sqrt{2}}
\end{align}
である。
よって、\(W\) の体積は
\begin{align}
&\left(\frac{2\pi\sqrt{3}}{3}+\frac{20}{3}\right)+\left\{14-6\sqrt{2}\left(\frac{3}{2}\alpha+\frac{1}{\sqrt{2}}\right)\right\}\pi\\
&\quad=\left(\frac{2\pi\sqrt{3}}{3}+\frac{20}{3}\right)+\left(8-9\sqrt{2}\alpha\right)\pi\\
&\quad=\frac{20}{3}+\left(\frac{2\sqrt{3}}{3}+8\right)\pi-9\sqrt{2}\pi\alpha
\end{align}
である。
考察と感想

(1)について
距離 \(\sqrt{3}\) までしか届かないい直進するレーザーを、原点からあらゆる方向に照射するイメージですね。\(S\) によって遮られる部分もありますが、立方体の表面のうち \(z=1\) なる面が除かれています。よって、立方体に対して、球から立方体を除いた部分の \(\displaystyle \frac{1}{6}\) を含めたものが \(V\) となります。
そのまま、
- 立方体の体積
- 球から立方体を除いた部分の \(\displaystyle \frac{1}{6}\) の体積
を合わせても良いですが、今回は立方体の \(\displaystyle \frac{1}{6}\) を2.の部分と合わせて計算しました。
(2)について
条件が複雑ですが、(1)の条件を満たす点 \({\rm P}\) は(2)の条件も満たすことがわかります。よって、\(V\) は \(W\) に含まれますから、\(W\) のうち \(V\) に含まれない部分の体積を求める方針で解きました。
回転体 の体積と、その回転する角の大きさや対称性を用いて計算できると良いと思います。

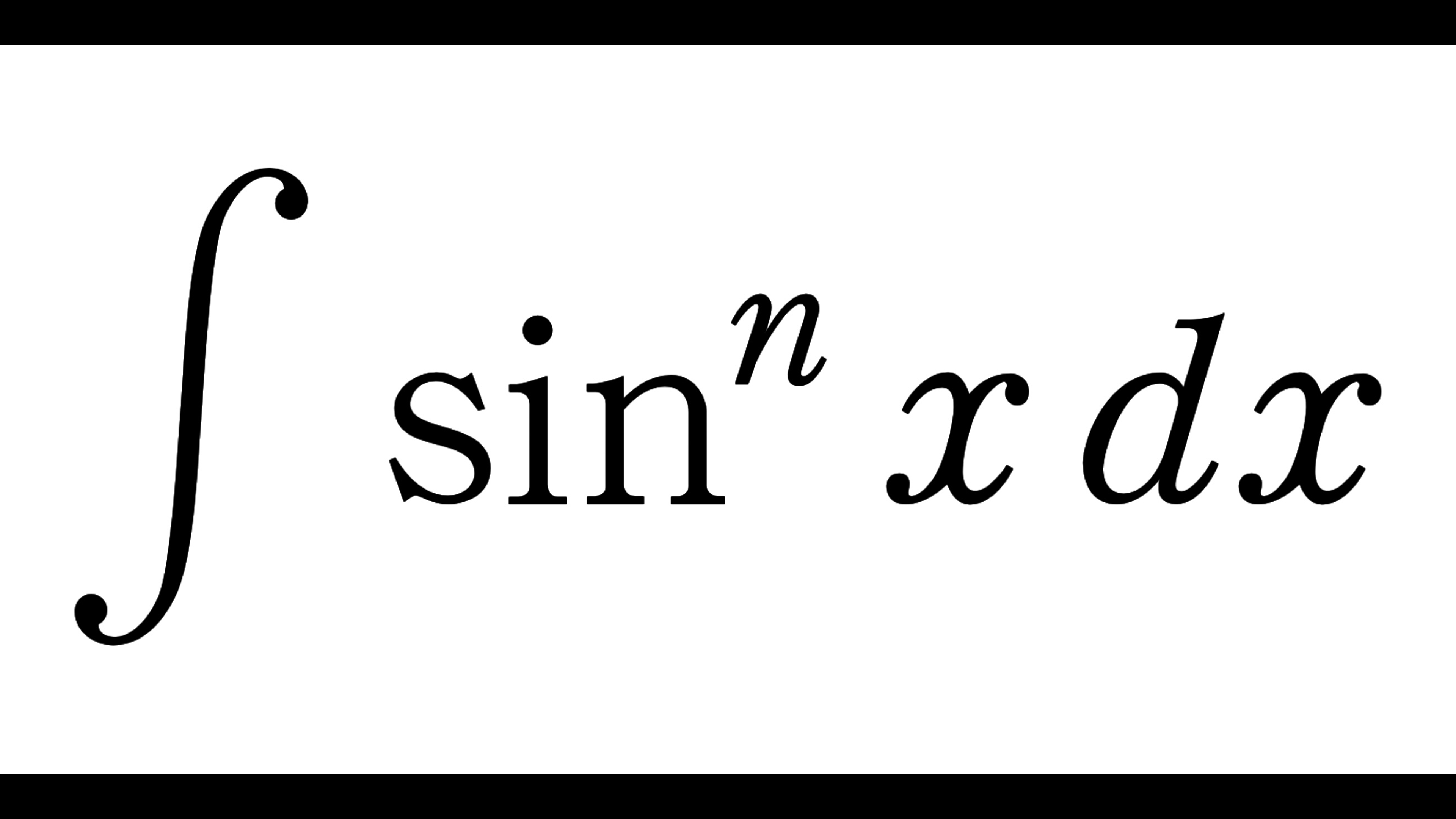
コメント