二項係数 \({}_{n}{\rm C}_{k}\) に関する公式をまとめました。
他にも紹介できる公式がありましたらコメント等で教えてください。
公式一覧

基本的な性質
公式 1
- \(\displaystyle {}_{n}{\rm C}_{k}={}_{n-1}{\rm C}_{k-1}+{}_{n-1}{\rm C}_{k}\)
- \(\displaystyle {}_{n}{\rm C}_{k}={}_{n}{\rm C}_{n-k}\)
- \(\displaystyle {}_{n}{\rm C}_{k}=\frac{n}{k}{}_{n-1}{\rm C}_{k-1}\)
二項定理の利用
公式 2
- \(\displaystyle \sum_{k=0}^n {}_{n}{\rm C}_{k}=2^n\)
- \(\displaystyle \sum_{k=0}^n (-1)^k{}_{n}{\rm C}_{k}=0\)
- \(\displaystyle \sum_{k=0}^{\left[n/2\right]} {}_{n}{\rm C}_{2k}=2^{n-1}\)
- \(\displaystyle \sum_{k=0}^{\left[(n-1)/2\right]} {}_{n}{\rm C}_{2k+1}=2^{n-1}\)
- \(\displaystyle \sum_{k=0}^{\left[n/2\right]} (-1)^k{}_{n}{\rm C}_{2k}=2^{\frac{n}{2}}\cos\frac{n\pi}{4}\)
- \(\displaystyle \sum_{k=0}^{\left[(n-1)/2\right]} (-1)^k{}_{n}{\rm C}_{2k+1}=2^{\frac{n}{2}}\sin\frac{n\pi}{4}\)
- \(\displaystyle \sum_{k=0}^{\left[n/3\right]} {}_{n}{\rm C}_{3k}=\frac{1}{3}\left(2^n+2\cos\frac{n\pi}{3}\right)\)
- \(\displaystyle \sum_{k=0}^{\left[n/4\right]} {}_{n}{\rm C}_{4k}=\frac{1}{2}\left(2^{n-1}+2^{\frac{n}{2}}\cos\frac{n\pi}{4}\right)\)
多項式の微分
公式 3
- \(\displaystyle \sum_{k=0}^n k{}_{n}{\rm C}_{k}=n2^{n-1}\)
- \(\displaystyle \sum_{k=0}^n k(k-1){}_{n}{\rm C}_{k}=n(n-1)2^{n-2}\)
- \(\displaystyle \sum_{k=0}^n k^2{}_{n}{\rm C}_{k}=n(n+1)2^{n-2}\)
- \(\displaystyle \sum_{k=0}^n k(k-1)(k-2){}_{n}{\rm C}_{k}\)\(\displaystyle \ =n(n-1)(n-2)2^{n-3}\)
- \(\displaystyle \sum_{k=0}^n k^3{}_{n}{\rm C}_{k}=n^2(n+3)2^{n-3}\)
- \(\displaystyle \sum_{k=0}^n (-1)^kk^n{}_{n}{\rm C}_{k}=(-1)^nn!\)
多項式の積分
公式 4
- \(\displaystyle \sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{k+1}=\frac{2^{n+1}-1}{n+1}\)
- \(\displaystyle \sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)}=\frac{2^{n+2}-n-3}{(n+1)(n+2)}\)
- \(\displaystyle \sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}\)\(\displaystyle \ =\frac{2^{n+4}-n^2-7n-14}{2(n+1)(n+2)(n+3)}\)
- \(\displaystyle \sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{k+1}=\frac{1}{n+1}\)
- \(\displaystyle \sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)}=\frac{1}{n+2}\)
- \(\displaystyle \sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}=\frac{1}{2(n+3)}\)
係数の比較
公式 5
- \(\displaystyle \sum_{k=0}^n ({}_{l}{\rm C}_{k})({}_{m}{\rm C}_{n-k})={}_{l+m}{\rm C}_{n}\)
- \(\displaystyle \sum_{k=0}^n \left({}_{n}{\rm C}_{k}\right)^2={}_{2n}{\rm C}_{n}\)
- \(\displaystyle \sum_{k=0}^n k\left({}_{n}{\rm C}_{k}\right)^2=\frac{n}{2}{}_{2n}{\rm C}_{n}\)
- \(\displaystyle \sum_{k=0}^{n} {}_{m+k}{\rm C}_{m}={}_{m+n+1}{\rm C}_{n}\)
- \(\displaystyle \sum_{k=0}^{n} {}_{n+k}{\rm C}_{n}={}_{2n+1}{\rm C}_{n}\)
その他(やや難〜難)
公式 6
- \(\displaystyle \sum_{k=0}^{\left[n/2\right]} {}_{n-k}{\rm C}_{n-2k}=F_{n+1}\)
- \(\displaystyle \sum_{k=0}^{2n} (-1)^k\left({}_{2n}{\rm C}_{k}\right)^3=(-1)^n\frac{(3n)!}{(n!)^3}\)
- \(\displaystyle \sum_{k=-\infty}^{\infty} (-1)^{k}\left({}_{a+b}{\rm C}_{a+k}\right)\left({}_{b+c}{\rm C}_{b+k}\right)\left({}_{c+a}{\rm C}_{c+k}\right)\)\(\displaystyle \ =\frac{(a+b+c)!}{a!b!c!}\)
→ 解説はこちら(標準的な高校数学の範囲を超えるものを含みます。)
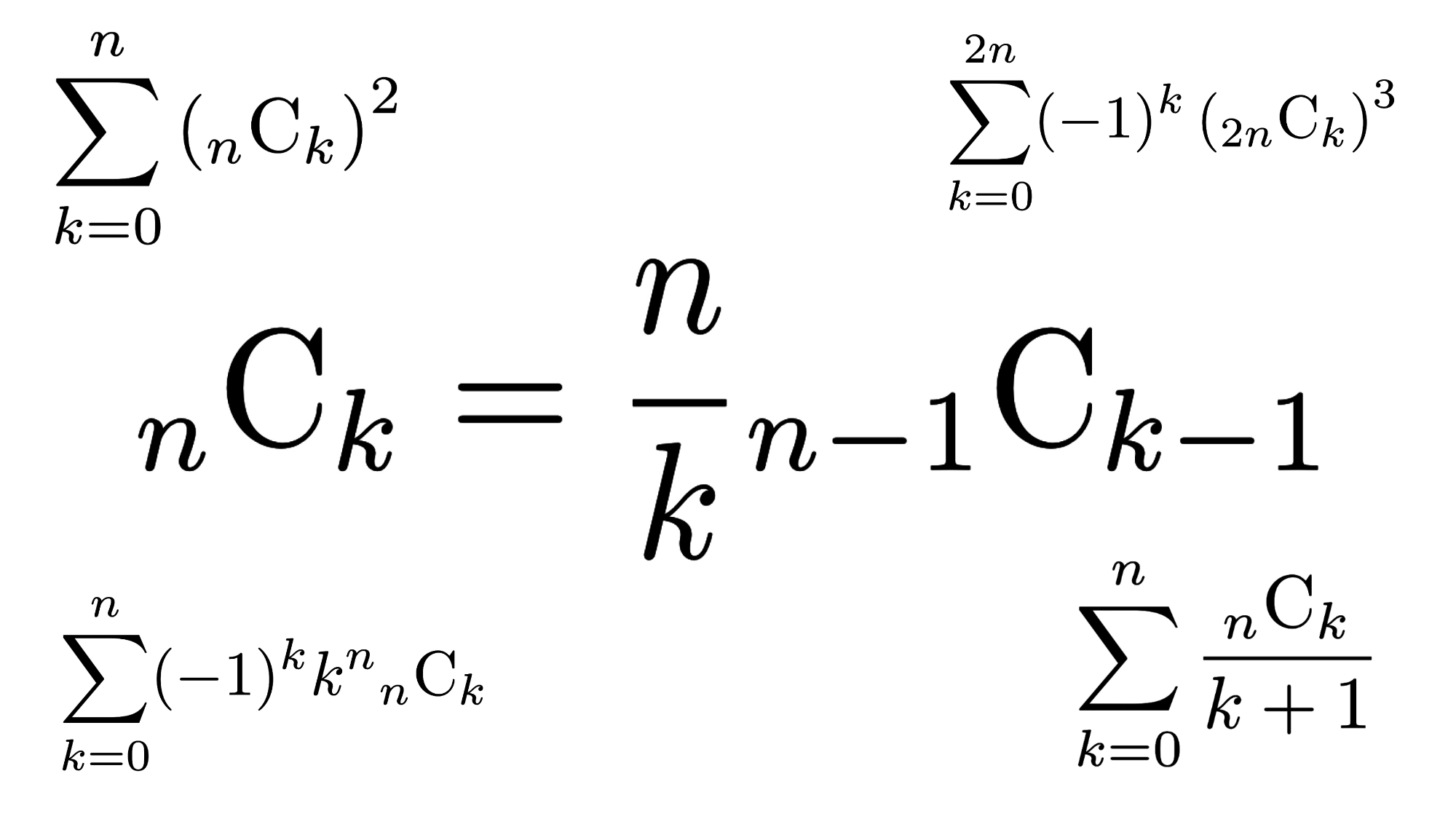
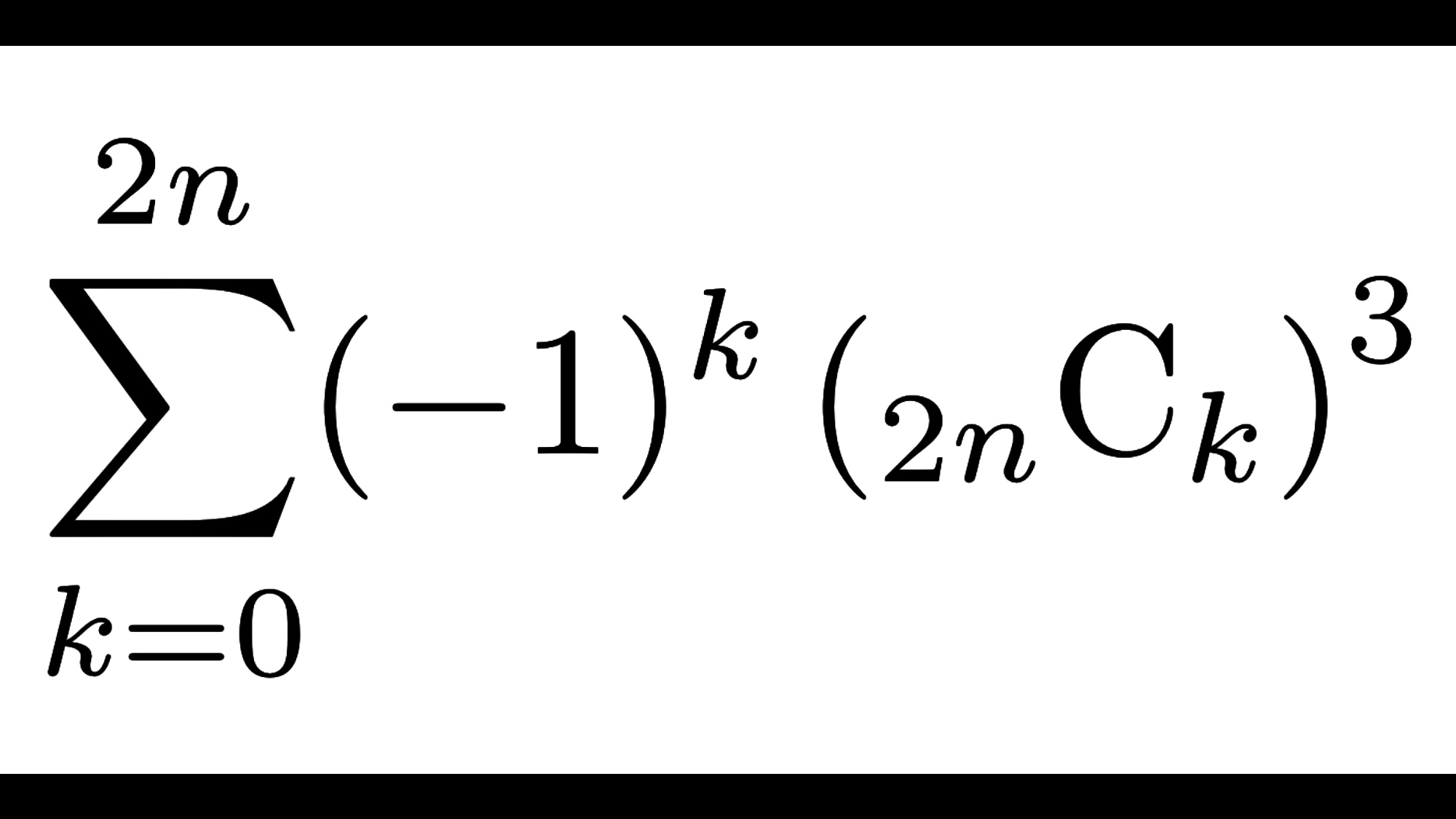

コメント