数学IIで習う 二項係数 \({}_{n}{\rm C}_{k}\) の和を求めます。今回は、数学IIIで学ぶ高次の項の定積分
\begin{align}
\int_0^t x^k dx&=\frac{t^{k+1}}{k+1}&&(k=0,1,2,\cdots)
\end{align}
を用います。今回、上記の \(t\) を改めて \(x\) とおく計算として
\begin{align}
\int_0^x x^k dx&=\frac{x^{k+1}}{k+1}&&(k=0,1,2,\cdots)
\end{align}
と書くことにします。これにより、以下の「多項式の積分」を扱ってゆきたいと思います。
他の公式は以下の リンク を参照してください。
積分法を用いた和の計算

\({}_{n}{\rm C}_{k}/(k+1)\)
$$\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{k+1}=\frac{2^{n+1}-1}{n+1}$$
証明の一例(その1)
\begin{align}
\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{k+1}
&=\sum_{k=0}^n \frac{{}_{n+1}{\rm C}_{k+1}}{n+1}\\
&=\sum_{k=-1}^n \frac{{}_{n+1}{\rm C}_{k+1}}{n+1}-\frac{{}_{n+1}{\rm C}_{0}}{n+1}\\
&=\frac{2^{n+1}}{n+1}-\frac{1}{n+1}\\
&=\frac{2^{n+1}-1}{n+1}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で積分すると
\begin{align}
\sum_{k=0}^n \frac{1}{k+1}\binom{n}{k}x^{k+1}
&=\int_0^x (1+x)^n dx\\
&=\frac{(1+x)^{n+1}-1}{n+1}
\end{align}
となる。これに \(x=1\) を代入することで
\begin{align}
\sum_{k=0}^n \frac{1}{k+1}\binom{n}{k}
=\frac{2^{n+1}-1}{n+1}
\end{align}
を得る。
\({}_{n}{\rm C}_{k}/(k+1)(k+2)\)
$$\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)}=\frac{2^{n+2}-n-3}{(n+1)(n+2)}$$
証明の一例(その1)
\begin{align}
&\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)}\\
&\qquad=\sum_{k=0}^n \frac{{}_{n+2}{\rm C}_{k+2}}{(n+1)(n+2)}\\
&\qquad=\sum_{k=-2}^n \frac{{}_{n+2}{\rm C}_{k+2}}{(n+1)(n+2)}-\frac{{}_{n+2}{\rm C}_{0}+{}_{n+2}{\rm C}_{1}}{(n+1)(n+2)}\\
&\qquad=\frac{2^{n+2}}{(n+1)(n+2)}-\frac{n+3}{(n+1)(n+2)}\\
&\qquad=\frac{2^{n+2}-n-3}{(n+1)(n+2)}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で \(2\) 回だけ積分すると
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)}\binom{n}{k}x^{k+2}\\
&\qquad=\int_0^x \frac{(1+x)^{n+1}-1}{n+1} dx\\
&\qquad=\frac{1}{n+1}\left\{\frac{(1+x)^{n+2}-1}{n+2}-x\right\}
\end{align}
となる。これに \(x=1\) を代入することで
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)}\binom{n}{k}\\
&\qquad=\frac{1}{n+1}\left(\frac{2^{n+2}-1}{n+2}-1\right)\\
&\qquad=\frac{2^{n+2}-n-3}{(n+1)(n+2)}
\end{align}
を得る。
\({}_{n}{\rm C}_{k}/(k+1)(k+2)(k+3)\)
$$\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}=\frac{2^{n+4}-n^2-7n-14}{2(n+1)(n+2)(n+3)}$$
証明の一例(その1)
\begin{align}
&\sum_{k=0}^n \frac{{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}\\
&\qquad=\sum_{k=0}^n \frac{{}_{n+3}{\rm C}_{k+3}}{(n+1)(n+2)(n+3)}\\
&\qquad=\sum_{k=-3}^n \frac{{}_{n+3}{\rm C}_{k+3}}{(n+1)(n+2)(n+3)}-\frac{{}_{n+3}{\rm C}_{0}+{}_{n+3}{\rm C}_{1}+{}_{n+3}{\rm C}_{2}}{(n+1)(n+2)(n+3)}\\
&\qquad=\frac{2^{n+3}}{(n+1)(n+2)(n+3)}-\frac{n^2+7n+14}{2(n+1)(n+2)(n+3)}\\
&\qquad=\frac{2^{n+4}-n^2-7n-14}{2(n+1)(n+2)(n+3)}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で \(3\) 回だけ積分すると
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)(k+3)}\binom{n}{k}x^{k+3}\\
&\qquad=\int_0^x \frac{1}{n+1}\left\{\frac{(1+x)^{n+2}-1}{n+2}-x\right\} dx\\
&\qquad=\frac{1}{n+1}\left[\frac{1}{n+2}\left\{\frac{(1+x)^{n+3}-1}{n+3}-x\right\}-\frac{x^2}{2}\right]
\end{align}
となる。これに \(x=1\) を代入することで
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)(k+3)}\binom{n}{k}\\
&\qquad=\frac{1}{n+1}\left\{\frac{1}{n+2}\left(\frac{2^{n+3}-1}{n+3}-1\right)-\frac{1}{2}\right\}\\
&\qquad=\frac{2^{n+4}-n^2-7n-14}{2(n+1)(n+2)(n+3)}
\end{align}
を得る。
\((-1)^k{}_{n}{\rm C}_{k}/(k+1)\)
$$\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{k+1}=\frac{1}{n+1}$$
証明の一例(その1)
\begin{align}
\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{k+1}
&=\sum_{k=0}^n \frac{(-1)^k{}_{n+1}{\rm C}_{k+1}}{n+1}\\
&=\sum_{k=-1}^n \frac{(-1)^k{}_{n+1}{\rm C}_{k+1}}{n+1}-\frac{-{}_{n+1}{\rm C}_{0}}{n+1}\\
&=0-\frac{-1}{n+1}\\
&=\frac{1}{n+1}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で積分すると
\begin{align}
\sum_{k=0}^n \frac{1}{k+1}\binom{n}{k}x^{k+1}
&=\int_0^x (1+x)^n dx\\
&=\frac{(1+x)^{n+1}-1}{n+1}
\end{align}
となる。これに \(x=-1\) を代入することで
\begin{align}
\sum_{k=0}^n \frac{(-1)^k}{k+1}\binom{n}{k}
=\frac{1}{n+1}
\end{align}
を得る。
\((-1)^k{}_{n}{\rm C}_{k}/(k+1)(k+2)\)
$$\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)}=\frac{1}{n+2}$$
証明の一例(その1)
\begin{align}
&\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)}\\
&\qquad=\sum_{k=0}^n \frac{(-1)^k{}_{n+2}{\rm C}_{k+2}}{(n+1)(n+2)}\\
&\qquad=\sum_{k=-2}^n \frac{(-1)^k{}_{n+2}{\rm C}_{k+2}}{(n+1)(n+2)}-\frac{{}_{n+2}{\rm C}_{0}-{}_{n+2}{\rm C}_{1}}{(n+1)(n+2)}\\
&\qquad=0-\frac{-n-1}{(n+1)(n+2)}\\
&\qquad=\frac{1}{n+2}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で \(2\) 回だけ積分すると
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)}\binom{n}{k}x^{k+2}\\
&\qquad=\int_0^x \frac{(1+x)^{n+1}-1}{n+1} dx\\
&\qquad=\frac{1}{n+1}\left\{\frac{(1+x)^{n+2}-1}{n+2}-x\right\}
\end{align}
となる。これに \(x=-1\) を代入することで
\begin{align}
&\sum_{k=0}^n \frac{(-1)^k}{(k+1)(k+2)}\binom{n}{k}\\
&\qquad=\frac{1}{n+1}\left(\frac{-1}{n+2}+1\right)\\
&\qquad=\frac{1}{n+2}
\end{align}
を得る。
\((-1)^k{}_{n}{\rm C}_{k}/(k+1)(k+2)(k+3)\)
$$\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}=\frac{1}{2(n+3)}$$
証明の一例(その1)
\begin{align}
&\sum_{k=0}^n \frac{(-1)^k{}_{n}{\rm C}_{k}}{(k+1)(k+2)(k+3)}\\
&\qquad=\sum_{k=0}^n \frac{(-1)^k{}_{n+3}{\rm C}_{k+3}}{(n+1)(n+2)(n+3)}\\
&\qquad=\sum_{k=-3}^n \frac{(-1)^k{}_{n+3}{\rm C}_{k+3}}{(n+1)(n+2)(n+3)}-\frac{-{}_{n+3}{\rm C}_{0}+{}_{n+3}{\rm C}_{1}-{}_{n+3}{\rm C}_{2}}{(n+1)(n+2)(n+3)}\\
&\qquad=0-\frac{-n^2-3n-2}{2(n+1)(n+2)(n+3)}\\
&\qquad=\frac{1}{2(n+3)}
\end{align}
証明の一例(その2)
二項定理より
\begin{align}
\sum_{k=0}^n \binom{n}{k}x^k=(1+x)^n
\end{align}
が成り立つ。両辺を区間 \([0,x]\) で \(3\) 回だけ積分すると
\begin{align}
&\sum_{k=0}^n \frac{1}{(k+1)(k+2)(k+3)}\binom{n}{k}x^{k+3}\\
&\qquad=\int_0^x \frac{1}{n+1}\left\{\frac{(1+x)^{n+2}-1}{n+2}-x\right\} dx\\
&\qquad=\frac{1}{n+1}\left[\frac{1}{n+2}\left\{\frac{(1+x)^{n+3}-1}{n+3}-x\right\}-\frac{x^2}{2}\right]
\end{align}
となる。これに \(x=-1\) を代入することで
\begin{align}
&\sum_{k=0}^n \frac{(-1)^k}{(k+1)(k+2)(k+3)}\binom{n}{k}\\
&\qquad=-\frac{1}{n+1}\left\{\frac{1}{n+2}\left(\frac{-1}{n+3}+1\right)-\frac{1}{2}\right\}\\
&\qquad=\frac{1}{2(n+3)}
\end{align}
を得る。
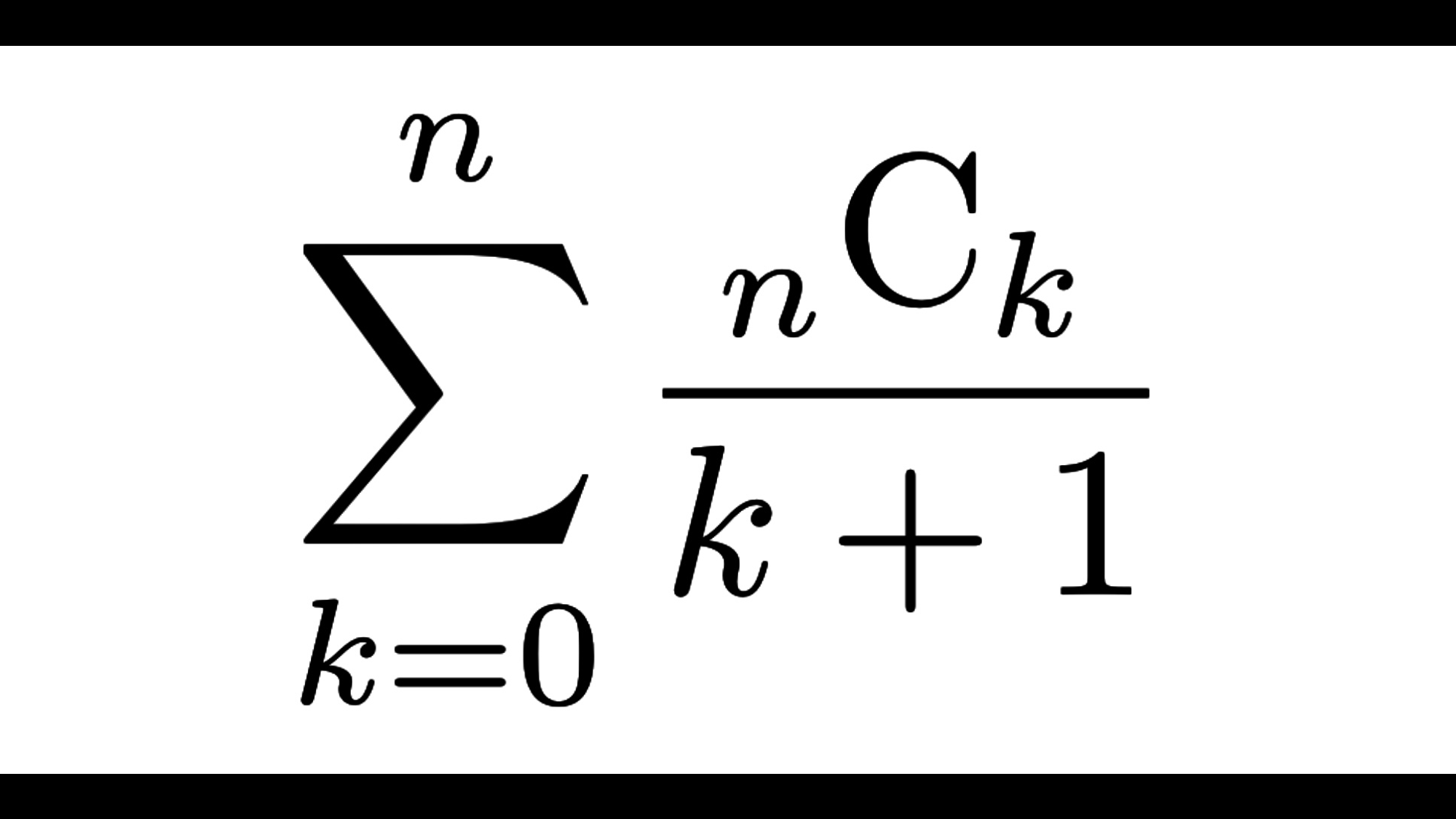
コメント