数学Bの「統計的な推測」の第4回として 母集団と標本 を扱います。(全7回)
今回は解説を含め、全4問を解いてゆきます。
復元抽出について
有限の母集団の変量 \(x\) が以下の分布をなしているとする。
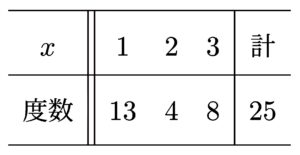
この母集団から復元抽出によって得られた大きさ \(20\) の無作為標本を $$X_1, X_2, \cdots, X_{20}$$ とし、その標本平均を \(\overline{X}\) とする。\(\overline{X}\) の期待値と標準偏差を求めよ。
解答例
母平均 \(m\) は
\begin{align}
m
&=\frac{1}{25}\left(1\cdot13+2\cdot4+3\cdot8\right)\\
&=\frac{45}{25}\\
&=\frac{9}{5}
\end{align}
また、母標準偏差 \(\sigma\) は
\begin{align}
\sigma
&=\sqrt{\frac{1}{25}\left(1^2\cdot13+2^2\cdot4+3^2\cdot8\right)-\left(\frac{9}{5}\right)^2}\\
&=\sqrt{\frac{20}{25}}\\
&=\frac{2\sqrt{5}}{5}
\end{align}
よって、標本平均を \(\overline{X}\) の期待値と標準偏差は
\begin{gather}
E(\overline{X})=m=\frac{9}{5}\\
\sigma(\overline{X})=\frac{\sigma}{\sqrt{20}}=\frac{1}{5}
\end{gather}
非復元抽出について
有限の母集団 \(\{1,1,2,3\}\) から非復元抽出によって得られた大きさ \(2\) の標本 \((X_1,X_2)\) を考える。このとき、標本平均 \(\displaystyle \overline{X}=\frac{X_1+X_2}{2}\) の確率分布を求めよ。
解答例
標本平均 \(\displaystyle \overline{X}=\frac{X_1+X_2}{2}\) を計算すると、下の表のようになる。
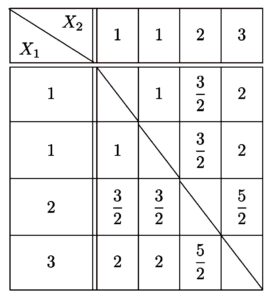
よって、各マスは等確率で起こるので、\(\overline{X}\) の確率分布は以下のようになる。
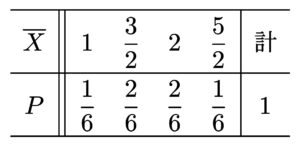
標本平均の期待値と標準偏差
\(1\) 個のさいころを \(1000\) 回投げる。このとき、出る目の平均 \(\overline{X}\) の期待値と標準偏差を求めよ。
解答例
さいころを \(1\) 回投げるときに出る目を \(X\) とする。このとき、
\begin{align}
P(X=k)&=\frac{1}{6}&&(k=1,2,\cdots,6)
\end{align}
である。よって、
\begin{align}
E(X)
&=\sum_{k=1}^6 k\frac{1}{6}\\
&=\frac{1}{6}\times\frac{1}{2}\cdot6\cdot7\\
&=\frac{7}{2}
\end{align}
また、
\begin{align}
E(X^2)
&=\sum_{k=1}^6 k^2\frac{1}{6}\\
&=\frac{1}{6}\times\frac{1}{6}\cdot6\cdot7\cdot13\\
&=\frac{91}{6}
\end{align}
より
\begin{align}
V(X)
&=E(X^2)-E(X)^2\\
&=\frac{91}{6}-\left(\frac{7}{2}\right)^2\\
&=\frac{91}{6}-\frac{49}{4}\\
&=\frac{35}{12}
\end{align}
この \(X\) の分布は母集団分布に一致する。
さて、さいころは \(1000\) 回投げていて、その標本平均が \(\overline{X}\) なので
\begin{align}
E(\overline{X})=\frac{7}{2}
\end{align}
また、\(\displaystyle V(\overline{X})=\frac{1}{1000}\cdot\frac{35}{12}\) より
\begin{align}
\sigma(\overline{X})=\sqrt{\frac{1}{1000}\cdot\frac{35}{12}}=\frac{\sqrt{42}}{120}
\end{align}
標本標準偏差の評価
ある県において、新生児の男子と女子の割合は等しいことが知られている。ある年の新生児の中から無作為に \(n\) 人抽出するとき、\(k\) 番目の新生児が男なら \(1\)、女なら \(0\) を対応させる確率変数を \(X_k\) とする。
(1)標本平均 \(\overline{X}\) の期待値 \(E(\overline{X})\) を求めよ。
(2)標本平均 \(\overline{X}\) の標準偏差 \(\sigma(\overline{X})\) を \(0.04\) 以下にするためには、標本の大きさ \(n\) はいくつ以上にする必要があるか。
解答例
(1)母平均 \(m\) は
\begin{align}
m
&=0\cdot0.5+1\cdot0.5\\
&=0.5
\end{align}
である。よって、求める期待値は
\begin{align}
E(\overline{X})=m=0.5
\end{align}
(2)母分散 \(\sigma^2\) は
\begin{align}
\sigma^2
&=(0^2\cdot0.5+1^2\cdot0.5)-0.5^2\\
&=0.5-0.25\\
&=0.25
\end{align}
よって、標本分散は
\begin{align}
\sigma^2(\overline{X})=\frac{0.25}{n}
\end{align}
これが \(0.04^2\) 以下になれば良いので
\begin{align}
\frac{0.25}{n}&\leq0.04^2\\
\frac{1}{4n}&\leq\frac{1}{625}\\
n&\geq\frac{625}{4}=156.25
\end{align}
これより、\(n\) は \(157\) 以上である必要がある。
最後に。
母集団分布に関わらず、母平均が \(m\)、母標準偏差が \(\sigma\) ならば標本平均 \(\overline{X}\) について
\begin{align}
E(\overline{X})&=m,&\sigma(\overline{X})&=\frac{\sigma}{\sqrt{n}}
\end{align}
が成り立ちます。つまり、標本の大きさ \(n\) を大きくするほど、標本平均の分布は母集団分布の平均を維持したまま標準偏差が小さくなってゆくのです。標本平均を考えることで、元の分布が平均 \(m\) の周りに集まってゆくのです。
お疲れ様でした。



コメント