今回は、虚数単位 \(i\) の \(i\) 乗である “ \(i^i\) ” の値に着目したいと思います。
- 例えば、\(3^4=81\) などの \({自然数}^{自然数}\) は必ず自然数になります。
- しかし、\(\displaystyle 2^{-3}=\frac{1}{8}\) となるので、\({整数}^{整数}\) は整数の範囲から飛び出すことがあります。
- また、\(5^{\frac{1}{2}}=\sqrt{5}\) となるので、\({有理数}^{有理数}\) は有理数の範囲から飛び出すことがあります。
このように、冪乗の計算をすると「構成する底と指数を含む数の範囲から値が飛び出る」が少なくありません。(ここで、“範囲” とは自然数、整数、有理数、実数、複素数などを表すものとします。)
さて、高校数学では扱わない冪乗の計算ですが、\(i^i\) の計算結果は次の選択肢のうちどれになると思いますか?
- 複素数の範囲から飛び出る。
- 複素数の範囲に留まるが、虚数となる。
- 複素数の範囲に留まり、特に実数となる。
さあ、この問の答えを確かめてみましょう!
冪乗を複素数へ拡張しよう。

高校数学までの知識の下、冪乗を複素数の範囲まで拡張しようと思います。順番としては
- 実関数に対するマクローリン展開について形式的に導入する。
- オイラーの公式を紹介して、指数関数 \(e^z\) を定義する。
- 対数関数 \(\log z\) を定義した後、一般の冪乗 \(a^b\) を定義する。
実数に対しては冪乗 \(a^b\) から対数関数 \(\log_a x\) を定義したので、その違いも感じられると良いと思います。
1. 実関数のマクローリン展開
何回でも微分できる関数 \(f(t)\) を考えます。
この関数 \(f(t)\) のことを “次数を無限大まで認めた多項式” によって表そうと試みます。つまり、
\begin{align}
f(t)
&=a_0+a_1t+a_2t^2+\cdots+a_nt^n+\cdots\\
&=\sum_{n=0}^{\infty}a_n t^n\tag{1}
\end{align}
と、無理矢理に書いてやろうとするのです。この形を認めるなら、例えば
- \(f(t)\) において \(t=0\) とすると \(f(0)=a_0\)
- \(f^\prime(t)\) において \(t=0\) とすると \(f^\prime(0)=a_1\)
- \(f^{\prime\prime}(t)\) において \(t=0\) とすると \(f^{\prime\prime}(0)=2a_2\)
などとなります。一般には
- \(f^{(n)}(t)\) において \(t=0\) とすると \(f^{(n)}(0)=n!a_n\)
となります。
よって、関数 \(f(t)\) が上の式 (1) の形の表示を認めるならば
\begin{align}
f(t)
&=f(0)+f^\prime(0)t+\frac{f^{\prime\prime}(0)}{2}t^2+\cdots+\frac{f^{(n)}(0)}{n!}t^n+\cdots\\
&=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}t^n\tag{2}
\end{align}
と書くことができます。これを、関数 \(f(t)\) の「マクローリン展開」と呼びます。
例えば、具体的に指数関数 \(e^t\) や三角関数 \(\sin t\) と \(\cos t\) のマクローリン展開を計算してみると、式 (2) より
\begin{align}
e^t&=1+t+\frac{1}{2}t^2+\cdots+\frac{1}{n!}t^n+\cdots\tag{3}\\
\sin t&=t-\frac{1}{3!}t^3+\frac{1}{5!}t^5+\cdots+\frac{(-1)^n}{(2n+1)!}t^{2n+1}+\cdots\tag{4}\\
\cos t&=1-\frac{1}{2!}t^2+\frac{1}{4!}t^4+\cdots+\frac{(-1)^n}{(2n)!}t^{2n}+\cdots\tag{5}
\end{align}
となります。
大学入試でもこれらを題材にした問題が存在するので、形に見覚えのある方もいるかもしれませんね。
2. オイラーの公式と指数関数
オイラーの公式の紹介
指数関数 \(e^t\) のマクローリン展開である式 (3) に、形式的に \(t=iy\) を代入してみます。ここで、\(i\) は虚数単位で、\(y\) は実数とします。
まず、\(e^{iy}\) を実部と虚部に分けると
\begin{align}
e^{iy}
&=1+iy+\frac{1}{2!}(iy)^2+\frac{1}{3!}(iy)^3+\frac{1}{4!}(iy)^4+\cdots\\
&=1+iy-\frac{1}{2!}y^2-\frac{1}{3!}iy^3+\frac{1}{4!}y^4+\cdots\\
&=\left(1-\frac{1}{2!}y^2+\frac{1}{4!}y^4+\cdots\right)+i\left(y-\frac{1}{3!}y^3+\frac{1}{5!}y^5+\cdots\right)
\end{align}
となります。この実部と虚部に着目すると、式 (4) 及び式 (5) より
\begin{align}
e^{iy}=\cos y+i\sin y\tag{6}
\end{align}
が成り立ちます。この公式 (6) を「オイラーの公式」と呼びます。
オイラーの公式によって、複素数 \(z\) の極形式は
\begin{align}
z=r(\cos\theta+i\sin\theta)=re^{i\theta}
\end{align}
と書くことができます。
指数関数の定義
このオイラーの公式を用いることで、複素数 \(z=x+iy\) に対して、指数関数
\begin{align}
e^z
&=e^xe^{iy}\\
&=e^x(\cos y+i\sin y)
\end{align}
が定義されます。
ここで、オイラーの公式より \(e^{iy}\) は \(y\) に関して周期 \(2\pi\) を持ちます。つまり、任意の複素数 \(z\) と整数 \(n\) について
\begin{align}
e^{z+2n\pi i}=e^z\tag{7}
\end{align}
が成り立ちます。
3. 対数関数による冪乗の定義
対数関数の定義
今、\(e\) を底とする(複素数に関する)指数関数は定義できています。対数関数は、複素数に対しても指数関数の逆関数のように定義したいですね。
複素数の変数 \(z\neq0\), \(w\) に対して
\begin{align}
w=\log z\ \Longleftrightarrow\ z=e^w\tag{8}
\end{align}
によって対数関数を定義します。
この対数関数を計算するために少し考察しましょう。式 (8) において
\begin{align}
z&=re^{i\theta},&w&=u+iv
\end{align}
とおいてみると $$re^{i\theta}=e^{u+iv}=e^u e^{iv}$$ となります。
- この両辺の絶対値を比較すると、\(r=e^u>0\) より \(u=\log r\) となります。
- また、偏角を比較すると式 (7) より \(v=\theta+2m\pi\) (\(m\in\mathbb{Z}\)) と書けます。( \(\mathbb{Z}\) は整数全体の集合を表します。)
以上より、\(0\) ではない複素数 \(z=re^{i\theta}\) に対して、具体的に
\begin{align}
\log z&=\log r +i(\theta+2m\pi)&&(m\in\mathbb{Z})
\end{align}
と計算できるのです。
例えば、\(z=1+i=\sqrt{2}e^{\frac{\pi}{4}i}\) に対して
\begin{align}
\log z
&=\log \sqrt{2} +i\left(\frac{\pi}{4}+2m\pi\right)&&(m\in\mathbb{Z})\\
&=\frac{1}{2}\log 2 +\frac{8m+1}{4}\pi i&&(m\in\mathbb{Z})
\end{align}
と計算できます。
これを見て、違和感がある方もいらっしゃるかもしれません。
そうです。関数値に整数 \(m\) が含まれており、値が唯一つには定まらないのです。このように、複数の値をとる関数のことを多価関数といいます。(これに対して、普通の関数を一価関数といいます。)
正の実数に対する対数関数は一価ですが、\(0\) でない複素数に拡張すると多価になってしまうのです。
冪乗の定義
今までに定義した指数関数と対数関数を用いて、複素数の冪乗を定義します。
まず、正の実数に対して、冪乗の底を変換する公式を思い出しましょう。対数の定義から直ちに従うこととして、\(a>0\) ならば \(a^b=e^{b\log a}\) が成り立ちますね。まさにこれを利用して、複素数に対する冪乗を定義するのです。
\(a\neq0\), \(b\) を複素数とします。このとき、
\begin{align}
a^b=e^{b\log a}
\end{align}
によって冪乗 \(a^b\) を定義します。
例えば、先程の結果を使うと
\begin{align}
i\log(1+i)
&=i\left(\frac{1}{2}\log 2 +\frac{8m+1}{4}\pi i\right)&&(m\in\mathbb{Z})\\
&=-\frac{8m+1}{4}\pi+\frac{i}{2}\log 2&&(m\in\mathbb{Z})
\end{align}
であるので、冪乗の定義より
\begin{align}
(1+i)^i
&=e^{i\log(1+i)}&&\\
&=e^{-\frac{8m+1}{4}\pi+\frac{i}{2}\log 2}&&(m\in\mathbb{Z})
\end{align}
と計算できるのです。
冪乗は対数関数を用いて定義されています。対数関数は多価でしたので、一見、定数に見える \((1+i)^i\) ですが、複数の値をとるということに注意しなければなりません。
さあ、準備は完了しました。冒頭の問に答えましょう!
冒頭の問の答えです!

まず、\(i\neq0\) ですので、冪乗 \(i^i\) は我々の見てきた意味で定義されます。そして、その値は複数とる(多価)でしょうが複素数です。これより、選択肢1は誤りです。
では、実際に計算してみましょう。
\(i=e^{\frac{\pi}{2}i}\) ですから
\begin{align}
\log i
&=\log 1 +i\left(\frac{\pi}{2}+2m\pi\right)&&(m\in\mathbb{Z})\\
&=\frac{4m+1}{2}\pi i&&(m\in\mathbb{Z})
\end{align}
と計算できます。よって、
\begin{align}
i\log i&=-\frac{4m+1}{2}\pi&&(m\in\mathbb{Z})
\end{align}
であるので、累乗の定義より
\begin{align}
i^i
=e^{i\log i}
=e^{-\frac{4m+1}{2}\pi}\quad(m\in\mathbb{Z})
\end{align}
と計算できるのです。
なんと、\(i^i\) は実数となりました。これにより選択肢2も誤りであって、選択肢3が正しいことがわかりましたね!
例えば、\(m=0\) の場合だけを考えると数値を計算できて
\begin{align}
i^i
=e^{-\frac{\pi}{2}}
=0.20787957635\cdots
\end{align}
となります。これを \(i^i\) の主値といいます。計算機に \(i^i\) を計算させると主値のみ返ってくるかもしれませんが、定義通りに計算すると無数の値をとります。
最後に。

いかがでしたでしょうか。今回は冪乗 \(i^i\) について、その値がどの数の範囲にあるかを考えてきました。答えは実数の範囲であることがわかりましたね。
最後に少し余談を。今回、簡単に導入した オイラーの公式 (6) ですが、\(y=\pi\) とすると $$e^{\pi i}+1=0$$ という「オイラーの等式」が得られます。これは、円周率 \(\pi\) とネイピア数 \(e\) と虚数単位 \(i\) (及び、\(0\) と \(1\) )が非常に簡潔な式で結びついており、「数学における最も美しい定理」とされています。
今回の定義で、さまざまな冪乗の計算をしてみると面白いと思います!(例えば、冒頭の \(5^{\frac{1}{2}}=\sqrt{5}\) の左辺を複素数の冪乗として考えると…?)
関連記事:【1+1=2】証明は難しい?「ペアノの公理を “ドミノ” で理解する。」
関連記事:【 (-1)×(-1)=1 の証明】なぜ「マイナス×マイナス=プラス」か説明せよ。
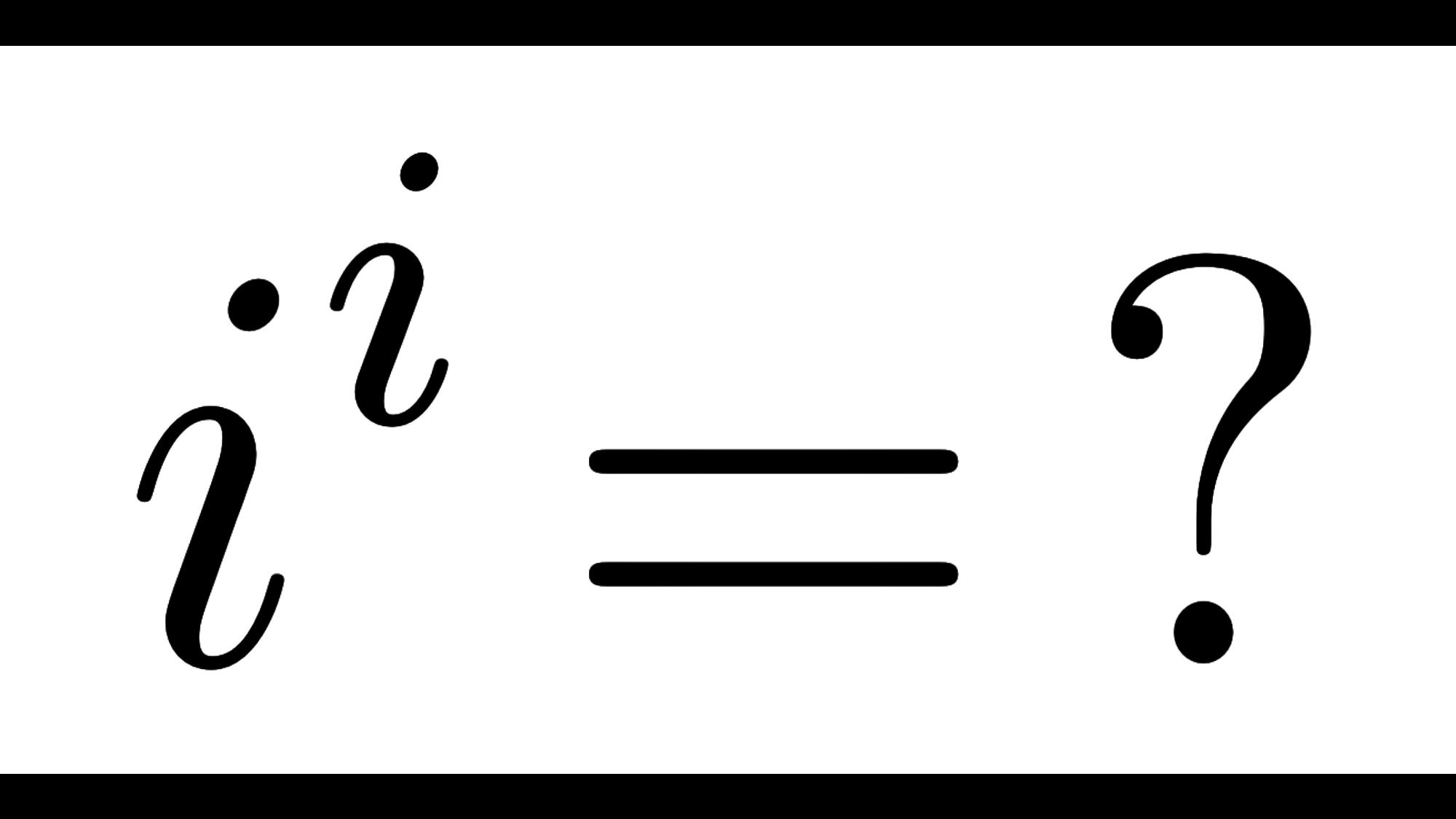


コメント