 数学IIIC
数学IIIC 「円周率 π は 3.05 よりも、3.14 よりも大きい!」ウォリスの公式で東大入試を解く。
今回は円周率 π が 3.05 より大きいこと、さらには、3.14 より大きいことを有限回の四則演算によって確認してゆきます。そんなことを可能にする道具が「ウォリスの公式」と呼ばれる無限積に関する公式です。
 数学IIIC
数学IIIC  数学IIIC
数学IIIC 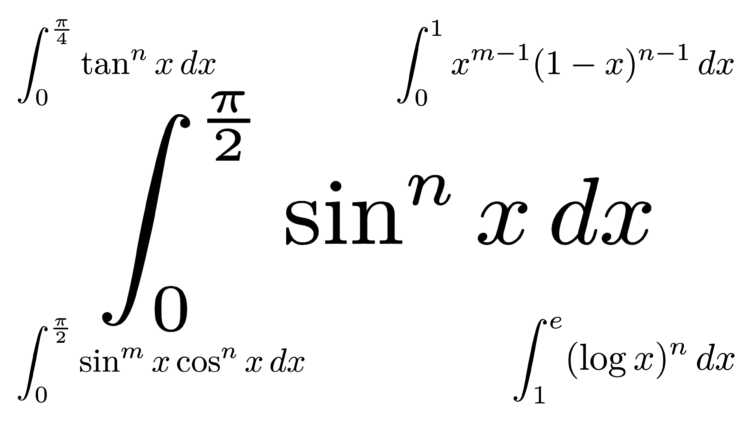 大学入試
大学入試  数学IIIC
数学IIIC  数学IIIC
数学IIIC  数学IIIC
数学IIIC 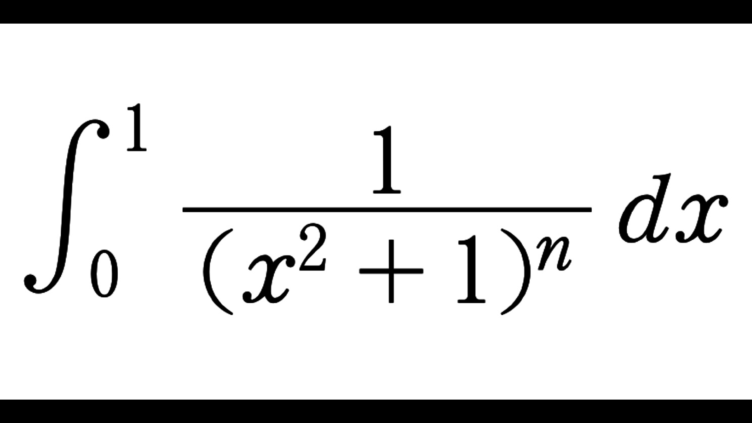 数学IIIC
数学IIIC 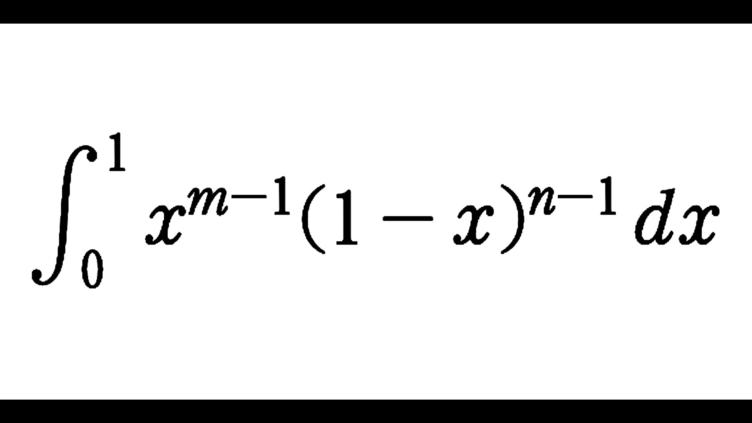 数学IIIC
数学IIIC 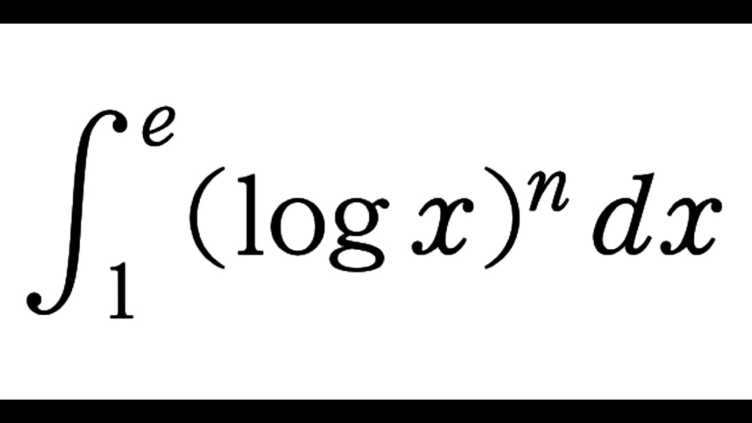 数学IIIC
数学IIIC 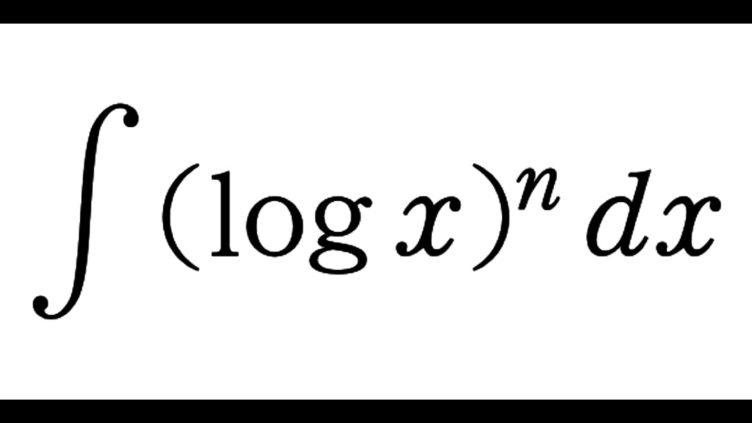 数学IIIC
数学IIIC