今回は「数列の和」の計算における部分分数分解のやり方を紹介したいと思います。
部分分数の和への計算では、恒等式の係数比較、具体的な数値の代入、裏ワザと呼ばれることのある ヘビサイドの展開定理 などの手法があります。本記事では、等式の証明ではなく計算途中の式変形を想定しているため、手法にはこだわらず柔軟に考えてゆきます。
私が意識している点を、一例として共有できればと思います。ただ手順を暗記するのではなく、頭を使って考え、手を動かしてゆきましょう!
練習問題 全11問

数列の和 \(\displaystyle \sum_{k=1}^na_k\) を求めてゆくわけですが、限られた \(a_k\) に対してしか公式は知りません。そこで、計算する際の解決策の一つとしては「隣接する項の差」を作る(階差と見做す)方法があります。具体的には、
$$a_k=f(k+1)-f(k)$$
もしくは
$$a_k=f(k)-f(k+1)$$
のような形を作ります。隣接する項の差を作ること を目標にして、部分分数分解を行います。
さて、思考の過程を明確にしながら以下の計算を行ってみましょう!
基本1 \(1/k(k+1)\)
まずは、簡単かもしれませんが、分子が \(1\) であるこの場合から。
\(\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)}\) を計算せよ。
部分分数への分解を考えますが、まずは分母から設定します。
$$\sum_{k=1}^n \frac{1}{k(k+1)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{\fbox{?}}{k}-\frac{\fbox{?}}{k+1}\right)$$
このように、分母を同じ因数ごとに分離します。この際、私は \(\fbox{?}\) の部分は空欄にして後から書き加えています。先頭の分数は、分数ごと書かないでおいて良いでしょう。
右辺を通分したらどうなるかを考えます。このときに
“とにかく分子から \(k\) を消去したい”
と思うわけです。その \(k\) さえ消去できれば残るは定数のみですから、それを適当な数で割れば分子は \(1\) とできるのです。
さて、準備した部分分数の \(k\) の係数は共に \(1\) です。差をとって分子から \(k\) を消去するためには、部分分数の分子も共に \(1\) であれば良いですね。
$$\sum_{k=1}^n \frac{1}{k(k+1)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{1}{k}-\frac{1}{k+1}\right)$$
この時点で通分したときの \(k\) の項は分子から消え去ります。もう気にしなくて良いです。
次に、右辺の分子の定数項のみ気にします。通分したとき分子に現れる定数のみ計算すると $$1-0=1$$ ですから、先頭の分数 \(\displaystyle \frac{1}{\fbox{?}}\) は \(\displaystyle \frac{1}{1}\) になるため、結局は書く必要がなく
$$\sum_{k=1}^n \frac{1}{k(k+1)}=\sum_{k=1}^n \left(\frac{1}{k}-\frac{1}{k+1}\right)$$
となります。
部分分数分解はここまでで終了です。もう計算できます。部分分数によって作り出した隣接する項は打ち消し合うので
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)}
&=\sum_{k=1}^n \left(\frac{1}{k}-\frac{1}{k+1}\right)\\
&=1-\frac{1}{n+1}\tag{L}\\
&=\frac{n}{n+1}
\end{align}
となります。
数学IIIにおいて、無限級数 $$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}$$ であった場合、部分和に対して式 \(({\rm L})\) の時点で極限をとると楽です。以下の「\(({\rm L})\)」も同じ “極限をとるサイン” と思ってください。
\(\displaystyle \sum_{k=1}^n\frac{1}{(k+1)(k+2)}\) を計算せよ。
基本2 \(1/(2k+1)(2k+3)\)
同じことを、数を変えてやってみます。
\(\displaystyle \sum_{k=1}^n\frac{1}{(2k+1)(2k+3)}\) を計算せよ。
まずは分母の設定から
$$\sum_{k=1}^n \frac{1}{(2k+1)(2k+3)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{\fbox{?}}{2k+1}-\frac{\fbox{?}}{2k+3}\right)$$
この際、私は分母が小さいものを前に書いています。今回の場合、\(2k+1\) の方が \(2k+3\) より小さいので \(\displaystyle \frac{1}{2k+1}\) を前にしています。先頭の分数 \(\displaystyle \frac{1}{\fbox{?}}\) を正にしたいからそうしているだけで、絶対そうしなければならないことではありません。
まず、準備した部分分数の \(k\) の係数は共に \(2\) です。差をとって分子から \(k\) を消去するためには、部分分数の分子も等しい必要があります。\(2\) と \(2\) でも良いですが、簡単な整数の比として \(1\) と \(1\) にしておきましょう。
$$\sum_{k=1}^n \frac{1}{(2k+1)(2k+3)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{1}{2k+1}-\frac{1}{2k+3}\right)$$
この時点で通分したときの \(k\) の項は分子から消え去ります。
次に、通分したとき分子に現れる定数のみ計算すると $$3-1=2$$ ですから、先頭の分数 \(\displaystyle \frac{1}{\fbox{?}}\) は \(\displaystyle \frac{1}{2}\) になり
$$\sum_{k=1}^n \frac{1}{(2k+1)(2k+3)}=\frac{1}{2}\sum_{k=1}^n \left(\frac{1}{2k+1}-\frac{1}{2k+3}\right)$$
となります。
部分分数分解はここまでで終了です。同様に、隣接する項は打ち消し合い
\begin{align}
\sum_{k=1}^n \frac{1}{(2k+1)(2k+3)}
&=\frac{1}{2}\sum_{k=1}^n \left(\frac{1}{2k+1}-\frac{1}{2k+3}\right)\\
&=\frac{1}{2} \left(\frac{1}{3}-\frac{1}{2n+3}\right)\tag{L}\\
&=\frac{n}{3(2n+3)}
\end{align}
となります。
\(\displaystyle \sum_{k=2}^n\frac{1}{k^2-1}\) を計算せよ。
標準1 \(1/(2k-1)(2k+3)\)
部分分数分解するとき、部分分数が隣接する必要はあったでしょうか。
\(\displaystyle \sum_{k=1}^n\frac{1}{(2k-1)(2k+3)}\) を計算せよ。
まずは分母の設定から
$$\sum_{k=1}^n \frac{1}{(2k-1)(2k+3)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{\fbox{?}}{2k-1}-\frac{\fbox{?}}{2k+3}\right)$$
さて、準備した部分分数の \(k\) の係数は共に \(2\) です。差をとって分子から \(k\) を消去するため、簡単な整数の比をとり \(1\) と \(1\) を採用します。
$$\sum_{k=1}^n \frac{1}{(2k-1)(2k+3)}=\frac{1}{\fbox{?}}\sum_{k=1}^n \left(\frac{1}{2k-1}-\frac{1}{2k+3}\right)$$
次に、通分したとき分子に現れる定数のみ計算すると $$3-(-1)=4$$ ですから、先頭の分数 \(\displaystyle \frac{1}{\fbox{?}}\) は \(\displaystyle \frac{1}{4}\) になり
$$\sum_{k=1}^n \frac{1}{(2k-1)(2k+3)}=\frac{1}{4}\sum_{k=1}^n \left(\frac{1}{2k-1}-\frac{1}{2k+3}\right)$$
となります。
部分分数分解はここまでで終了です。準備した部分分数である \(\displaystyle \frac{1}{2k-1}\) と \(\displaystyle \frac{1}{2k+3}\) は隣接していませんでした。\(k\) の値を \(2\) だけ変えれば一致するので “隣の隣” ですね。よって、\(n\geq2\) とすると
\begin{align}
\sum_{k=1}^n \frac{1}{(2k-1)(2k+3)}
&=\frac{1}{4}\sum_{k=1}^n \left(\frac{1}{2k-1}-\frac{1}{2k+3}\right)\\
&=\frac{1}{4} \left(\frac{1}{1}+\frac{1}{3}-\frac{1}{2n+1}-\frac{1}{2n+3}\right)\tag{L}\\
&=\frac{n(4n+5)}{3(2n+1)(2n+3)}
\end{align}
となります。これは \(n=1\) のときも成り立ちます。
\(\displaystyle \sum_{k=1}^n\frac{1}{k(k+2)}\) を計算せよ。
標準2 \(1/k(k+1)(k+2)\)
分母に因数が \(3\) つある場合を考えてみましょう。
\(\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)(k+2)}\) を計算せよ。
分母の設定についてですが、分解を完全に行おうとすると、部分分数は
\begin{align}
\frac{1}{k}&,&
\frac{1}{k+1}&,&
\frac{1}{k+2}&
\end{align}
の三つの定数倍を用いたものが想定されます。一方、我々が目指しているのは
$$f(k)-f(k+1)$$
のような二つの差を考えることです。これより、部分分数への段階的な分解として
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)(k+2)}
=\frac{1}{\fbox{?}}\sum_{k=1}^n \left\{\frac{\fbox{?}}{k(k+1)}-\frac{\fbox{?}}{(k+1)(k+2)}\right\}
\end{align}
を目指す形に設定します。
ここで、「部分分数の分子は定数ではなく \(k\) の \(1\) 次式の形をしているのでは?」という疑問を持った方もいると思います。今、
\begin{align}
\frac{1}{k(k+1)(k+2)}
&=\frac{\fbox{?}}{k(k+1)}-\frac{\fbox{?}}{(k+1)(k+2)}\\
&=\frac{1}{k+1}\left(\frac{\fbox{?}}{k}-\frac{\fbox{?}}{k+2}\right)
\end{align}
であるので、実質 $$\frac{1}{k(k+2)}=\frac{\fbox{?}}{k}-\frac{\fbox{?}}{k+2}$$ になっているのです。よって、分子の \(\fbox{?}\) は定数で十分なのです。分母に共通する因数があるときは要注意ですね。また、その部分分数を \(\displaystyle \frac{1}{k+1}\) が繋いで隣接する項の差になっています。
共通する因数の \((k+1)\) は一旦、無視します。
分母の残りの因数である \(k\) と \((k+2)\) において、\(k\) の係数は共に \(1\) です。差をとって分子から \(k\) を消去するため、分子も共に \(1\) にします。
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)(k+2)}
=\frac{1}{\fbox{?}}\sum_{k=1}^n \left\{\frac{1}{k(k+1)}-\frac{1}{(k+1)(k+2)}\right\}
\end{align}
次に、通分したとき分子に現れる定数のみ計算すると $$2-0=2$$ ですから、先頭の分数 \(\displaystyle \frac{1}{\fbox{?}}\) は \(\displaystyle \frac{1}{2}\) になり
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)(k+2)}
=\frac{1}{2}\sum_{k=1}^n \left\{\frac{1}{k(k+1)}-\frac{1}{(k+1)(k+2)}\right\}
\end{align}
となります。
部分分数分解はここまでで終了です。隣接する項は打ち消し合うので
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)(k+2)}
&=\frac{1}{2}\sum_{k=1}^n \left\{\frac{1}{k(k+1)}-\frac{1}{(k+1)(k+2)}\right\}\\
&=\frac{1}{2}\left\{\frac{1}{1\times2}-\frac{1}{(n+1)(n+2)}\right\}\tag{L}\\
&=\frac{n(n+3)}{4(n+1)(n+2)}
\end{align}
となります。
\(\displaystyle \sum_{k=1}^n\frac{1}{(2k-1)(2k+1)(2k+3)}\) を計算せよ。
応用1 \(1/k(k+1)(k+3)\)
一つ前の問題と少し違いますが、どのように解きますか?
\(\displaystyle \sum_{k=1}^n\frac{1}{k(k+1)(k+3)}\) を計算せよ。
分母の設定についてですが、小さい因数 \(k\) を除いた \(\displaystyle \frac{1}{(k+1)(k+3)}\) と大きい因数 \((k+3)\) を除いた \(\displaystyle \frac{1}{k(k+1)}\) に分解しても、見通しが良くありません。それは、分母の因数が
\begin{align}
k&,&
k+1&,&
k+3&
\end{align}
のように一個 \((k+2)\) が抜けているからです。それを補って、連続した因数を作りましょう。
\begin{align}
&\frac{1}{k(k+1)(k+3)}\\
&\quad=\frac{k+2}{k(k+1)(k+2)(k+3)}\\
&\quad=\frac{k}{k(k+1)(k+2)(k+3)}+\frac{2}{k(k+1)(k+2)(k+3)}\\
&\quad=\frac{1}{(k+1)(k+2)(k+3)}+\frac{2}{k(k+1)(k+2)(k+3)}
\end{align}
この二つの項をそれぞれ分解すると
\begin{align}
\frac{1}{k(k+1)(k+3)}
&=\frac{1}{2}\left\{\frac{1}{(k+1)(k+2)}-\frac{1}{(k+2)(k+3)}\right\}\\
&\qquad+\frac{2}{3}\left\{\frac{1}{k(k+1)(k+2)}-\frac{1}{(k+1)(k+2)(k+3)}\right\}
\end{align}
よって、\(k=1,2,\cdots,n\) の和を考えると
\begin{align}
\sum_{k=1}^n \frac{1}{k(k+1)(k+3)}
&=\frac{1}{2}\left\{\frac{1}{2\times3}-\frac{1}{(n+2)(n+3)}\right\}\\
&\qquad+\frac{2}{3}\left\{\frac{1}{1\times2\times3}-\frac{1}{(n+1)(n+2)(n+3)}\right\}\tag{L}\\
&=\frac{7}{36}-\frac{3n+7}{6(n+1)(n+2)(n+3)}
\end{align}
となります。
\(\displaystyle \sum_{k=1}^n\frac{1}{k(k+2)(k+3)}\) を計算せよ。
応用2 \(1/k^2(k+1)(k+2)^2\)
同様に、次の問題を解いてみましょう。
\(\displaystyle \sum_{k=1}^n\frac{1}{k^2(k+1)(k+2)^2}\) を計算せよ。
分母の因数のうち、\((k+1)\) が一個足りないので補います。
\begin{align}
\frac{1}{k^2(k+1)(k+2)^2}
&=\frac{k+1}{k^2(k+1)^2(k+2)^2}
\end{align}
先ほどのように分子を \(k\) と \(1\) に分けて考えると、\(k\) を約分したときに分母の次数が再び崩れてしまいます。別の方法を考えましょう。
分母が \(k(k+1)(k+2)\) のときは、部分分数の分母は \(k(k+1)\) と \((k+1)(k+2)\) にして差を考えました。それを参考にしてみると
\begin{gather}
\frac{1}{k^2(k+1)^2}=\frac{k^2+4k+4}{k^2(k+1)^2(k+2)^2},\\
\frac{1}{(k+1)^2(k+2)^2}=\frac{k^2}{k^2(k+1)^2(k+2)^2}
\end{gather}
であって、これらの分子の差は \((k+1)\) の定数倍になります!
これは、試行錯誤が必要なステップだと思います。
これより
\begin{align}
\frac{1}{k^2(k+1)(k+2)^2}=\frac{1}{4}\left\{\frac{1}{k^2(k+1)^2}-\frac{1}{(k+1)^2(k+2)^2}\right\}
\end{align}
よって、\(k=1,2,\cdots,n\) の和を考えると
\begin{align}
\sum_{k=1}^n \frac{1}{k^2(k+1)(k+2)^2}
&=\frac{1}{4}\left\{\frac{1}{1^2\times2^2}-\frac{1}{(n+1)^2(n+2)^2}\right\}\tag{L}\\
&=\frac{1}{16}-\frac{1}{4(n+1)^2(n+2)^2}
\end{align}
となります。
積分の計算について
今回は、部分分数分解がよく扱われるテーマのうち「数列の和」について考えてきました。
もう一つのテーマである「積分の計算」に関しては、以下の記事 をご覧ください
今回、隣接する項の差を作ること を目標にしたために現れなかったものが、積分の計算ができる形を作ること を目標とすることで現れてきます。\(2\) 乗の因数を含む場合や因数分解が実数の範囲で終わっている \(2\) 次式を含む場合など、公式がなぜそうなるのかまで説明してゆきます。
部分分数分解の理論については以下の関連記事をご覧ください。
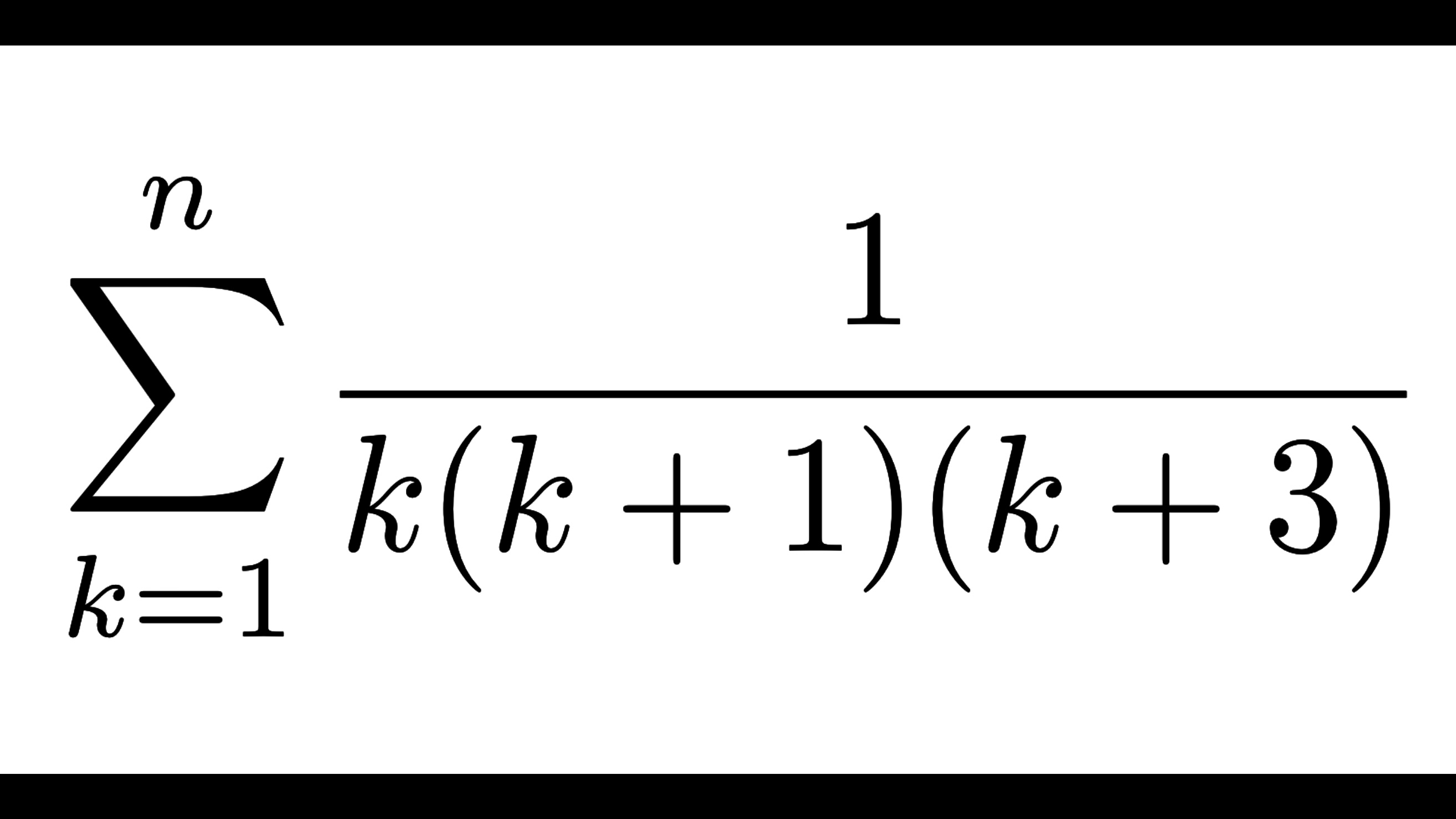
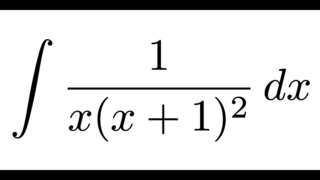
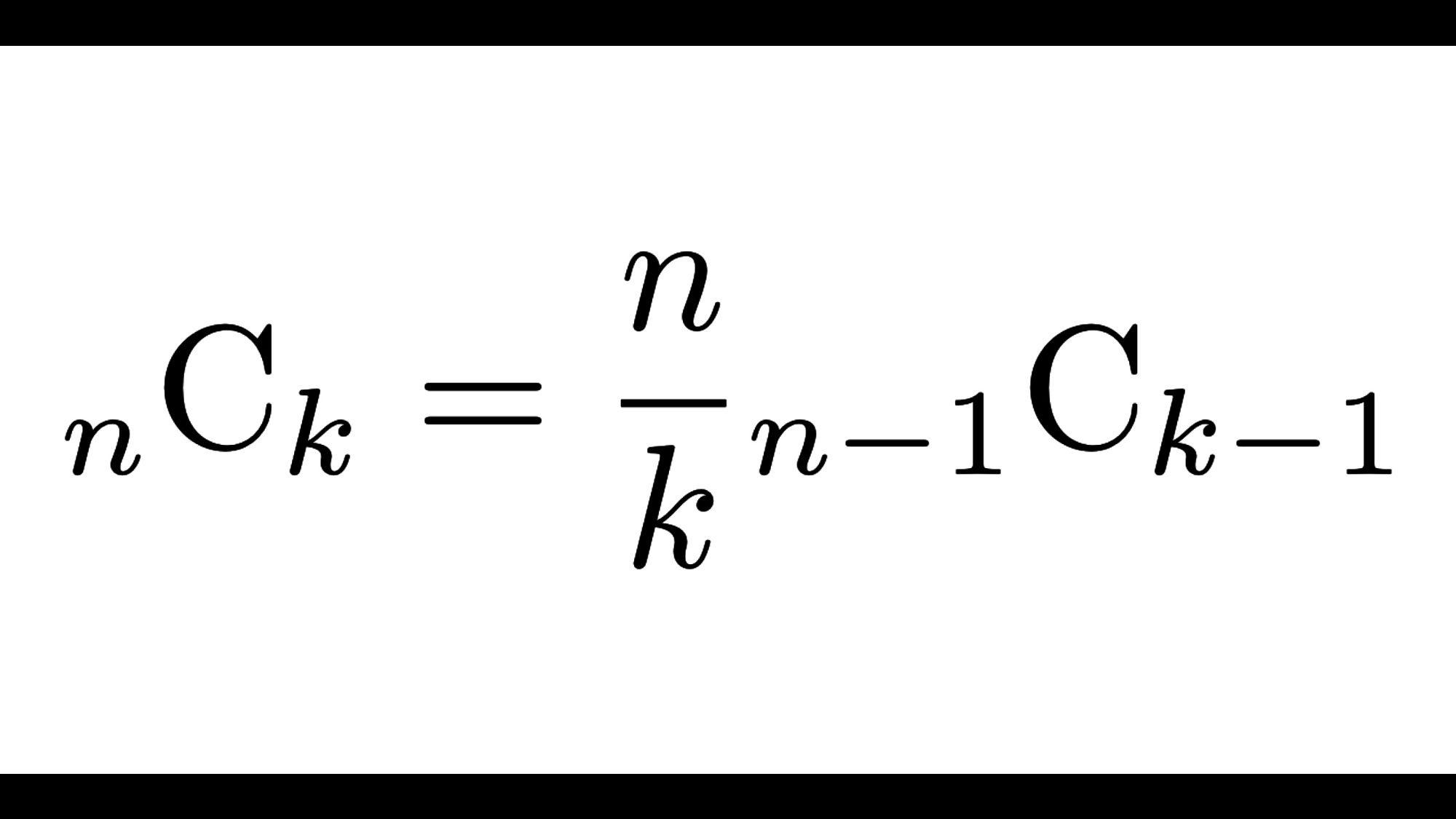
コメント