みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の定積分
\begin{align}
F_n&=\int_0^{\infty} x^ne^{-x}\,dx
\end{align}
を考える。但し、\(x^0=1\) とする。
(1)\(F_0\) を求めよ。
(2)\(F_n\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle F_0=1\)
(2)\(\displaystyle F_n=n!\)
解説

\(F_0\) を求める。
まず、\(x^0=1\) と約束していたので
\begin{align}
F_0
&=\int_0^{\infty} e^{-x}\,dx\\
&=\left[-e^{-x}\right]_0^{\infty}\\
&=-0-(-1)\\
&=1
\end{align}
となります。
\(F_n\) の一般項を求める。
\(n\geq1\) として部分積分を行います。
\begin{align}
F_n
&=\int_0^{\infty} x^ne^{-x}\,dx\\
&=\left[x^n(-e^{-x})\right]_0^{\infty}-\int_0^{\infty} nx^{n-1}(-e^{-x})\,dx\\
&=0+n\int_0^{\infty} x^{n-1}e^{-x}\,dx\\
&=nF_{n-1}
\end{align}
この両辺を \(n!\) で割ることで、数列 \(\displaystyle \left\{\frac{F_n}{n!}\right\}\) は定数列となります。
例えば、\(n=0\) のときを考えると
\begin{align}
\frac{F_n}{n!}=\frac{F_0}{0!}=1
\end{align}
すなわち
\begin{align}
F_n=n!
\end{align}
を得ます。
最後に

今回登場した階乗の一般化として「ガンマ関数」と呼ばれる関数があります。具体的には、実部が正である複素数 \(z\) に対して
\begin{align}
\Gamma(z)=\int_0^\infty t^{z-1}e^{-t}\,dt
\end{align}
と定義されます。
今回の定積分
\begin{align}
F_n&=\int_0^{\infty} x^ne^{-x}\,dx
\end{align}
と見比べると、正の整数 \(n\) に対して
\begin{align}
\Gamma(n)=F_{n-1}=(n-1)!
\end{align}
が成り立ちます。
これを、実部が正であれば複素数の範囲で考えても良いとしたのがガンマ関数です。
似ている形の定積分を以下の記事で扱っています。
関連 : 数学IIICカテゴリー
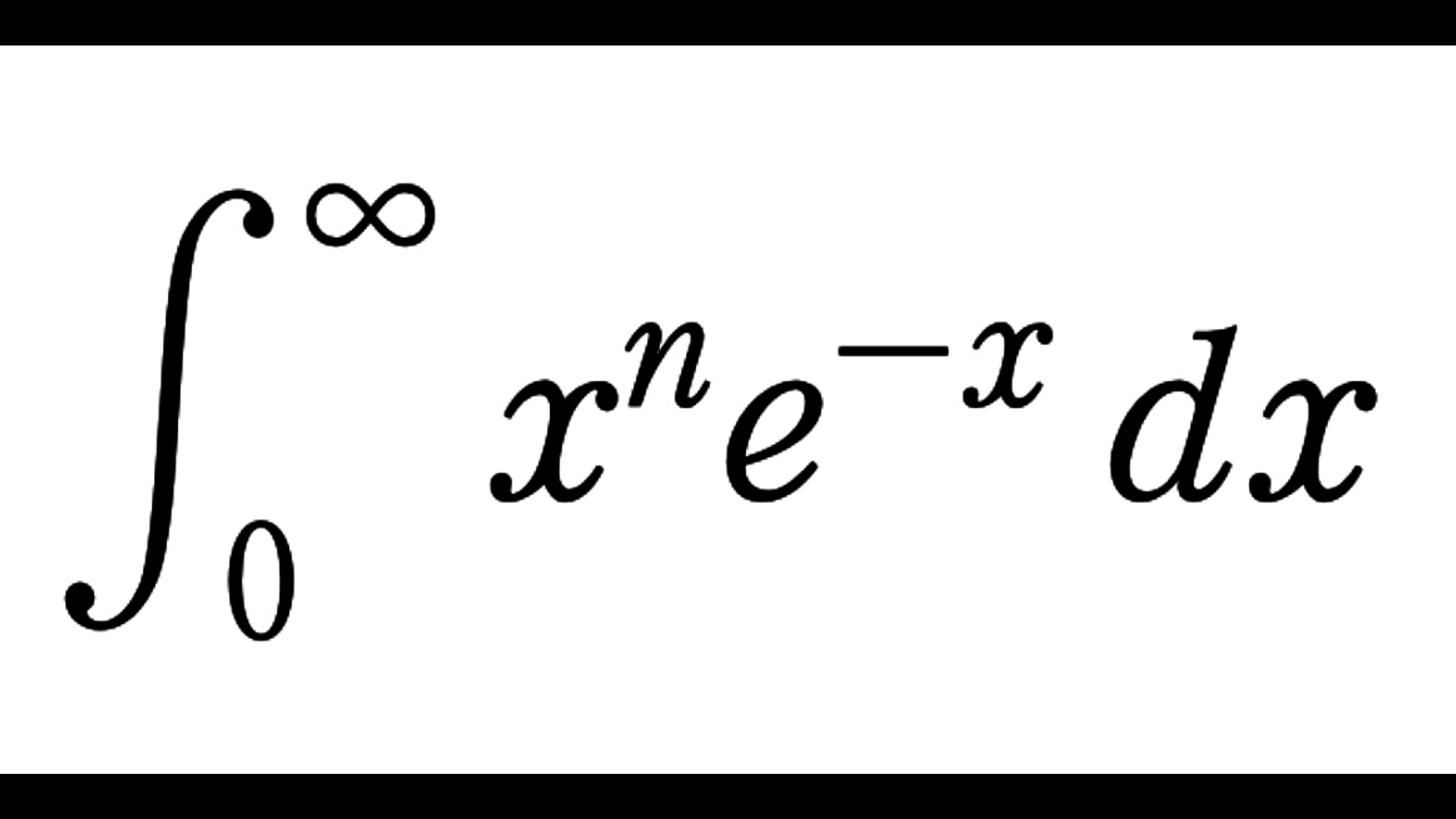
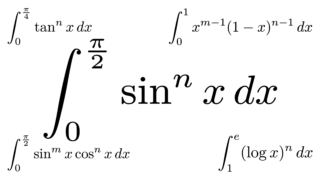
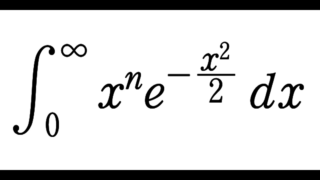
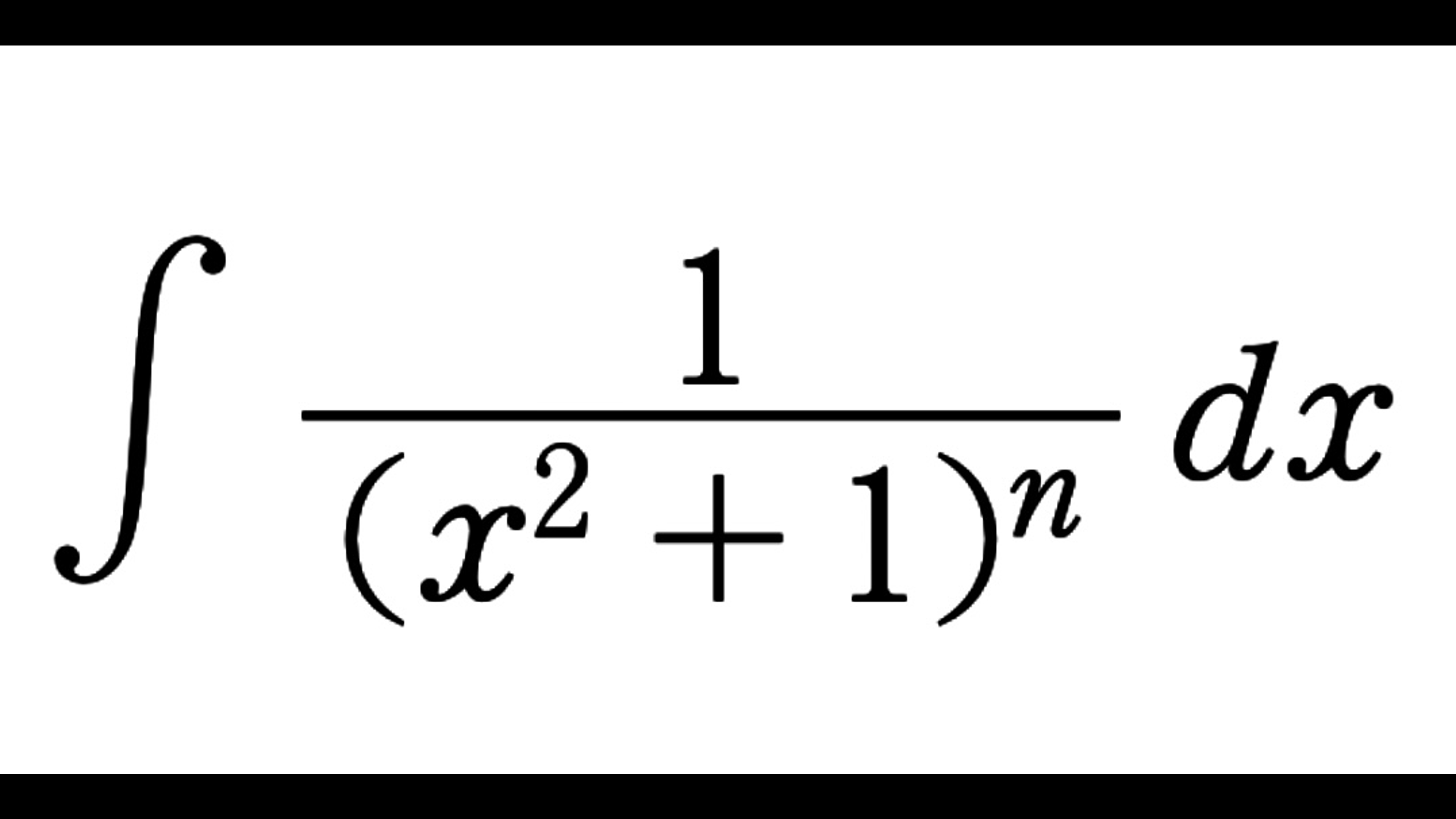
コメント