みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の定積分
\begin{align}
G_n&=\int_0^{\infty} x^ne^{-\frac{x^2}{2}}\,dx
\end{align}
を考える。但し、\(x^0=1\) とする。
(1)\(G_0\) を求めよ。
(2)\(G_1\) を求めよ。
(3)\(n\geq2\) に対して \(G_n\) を \(G_{n-2}\) で表すことで、\(G_n\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle G_0=\sqrt{\frac{\pi}{2}}\)
(2)\(\displaystyle G_1=1\)
(3)\(n\) が偶数のとき
\begin{align}
G_n=(n-1)!!\times\sqrt{\frac{\pi}{2}}
\end{align}
\(n\) が奇数のとき
\begin{align}
G_n=(n-1)!!
\end{align}
解説

\(G_0\) を求める。
まず、\(x^0=1\) と約束していたので
\begin{align}
G_0=\int_0^{\infty} e^{-\frac{x^2}{2}}\,dx
\end{align}
となります。ここで、ガウス積分 より
\begin{align}
G_0=\frac{1}{2}\times\sqrt{2\pi}=\sqrt{\frac{\pi}{2}}
\end{align}となります。
\(G_1\) を求める。
\(n=1\) とすることで
\begin{align}
G_1
&=\int_0^{\infty} xe^{-\frac{x^2}{2}}\,dx\\
&=\left[-e^{-\frac{x^2}{2}}\right]_0^{\infty}\\
&=-0-(-1)\\
&=1
\end{align}
となります。
\(G_n\) の一般項を求める。
\(n\geq2\) として部分積分を行います。
\begin{align}
G_n
&=\int_0^{\infty} x^{n-1}xe^{-\frac{x^2}{2}}\,dx\\
&=\left[x^{n-1}(-e^{-\frac{x^2}{2}})\right]_0^{\infty}-\int_0^{\infty} (n-1)x^{n-2}(-e^{-\frac{x^2}{2}})\,dx\\
&=0+(n-1)\int_0^{\infty} x^{n-2}e^{-\frac{x^2}{2}}\,dx\\
&=(n-1)G_{n-2}
\end{align}
この両辺を \((n-1)!!\) で割ることで、数列 \(\displaystyle \left\{\frac{G_n}{(n-1)!!}\right\}\) は \(n\) が偶数と奇数で各々一定の値をとります。
\(n\) が偶数のとき
例えば、\(n=0\) のときを考えると
\begin{align}
\frac{G_n}{(n-1)!!}=\frac{G_0}{(-1)!!}=\sqrt{\frac{\pi}{2}}
\end{align}
すなわち
\begin{align}
G_n=(n-1)!!\times\sqrt{\frac{\pi}{2}}
\end{align}
を得ます。
\(n\) が奇数のとき
例えば、\(n=1\) のときを考えると
\begin{align}
\frac{G_n}{(n-1)!!}=\frac{G_1}{0!!}=1
\end{align}
すなわち
\begin{align}
G_n=(n-1)!!
\end{align}
を得ます。
最後に

標準正規分布に従う確率変数 \(X\) の確率密度関数は
\begin{align}
f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
\end{align}
です。このとき、\(n\) 次のモーメントと呼ばれる
\begin{align}
E(X^n)
&=\int_{-\infty}^{\infty} x^nf(x)\,dx\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} x^ne^{-\frac{x^2}{2}}\,dx
\end{align}
を考えると、\(n\) が奇数のとき \(E(X^n)=0\) となります。
一方、\(n\) が偶数のとき、今回の結果を用いれば
\begin{align}
E(X^n)
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} x^ne^{-\frac{x^2}{2}}\,dx\\
&=\frac{2}{\sqrt{2\pi}}\int_0^{\infty} x^ne^{-\frac{x^2}{2}}\,dx\\
&=\frac{2}{\sqrt{2\pi}}\times(n-1)!!\times\sqrt{\frac{\pi}{2}}\\
&=(n-1)!!
\end{align}
がわかります。
関連 : 数学IIICカテゴリー
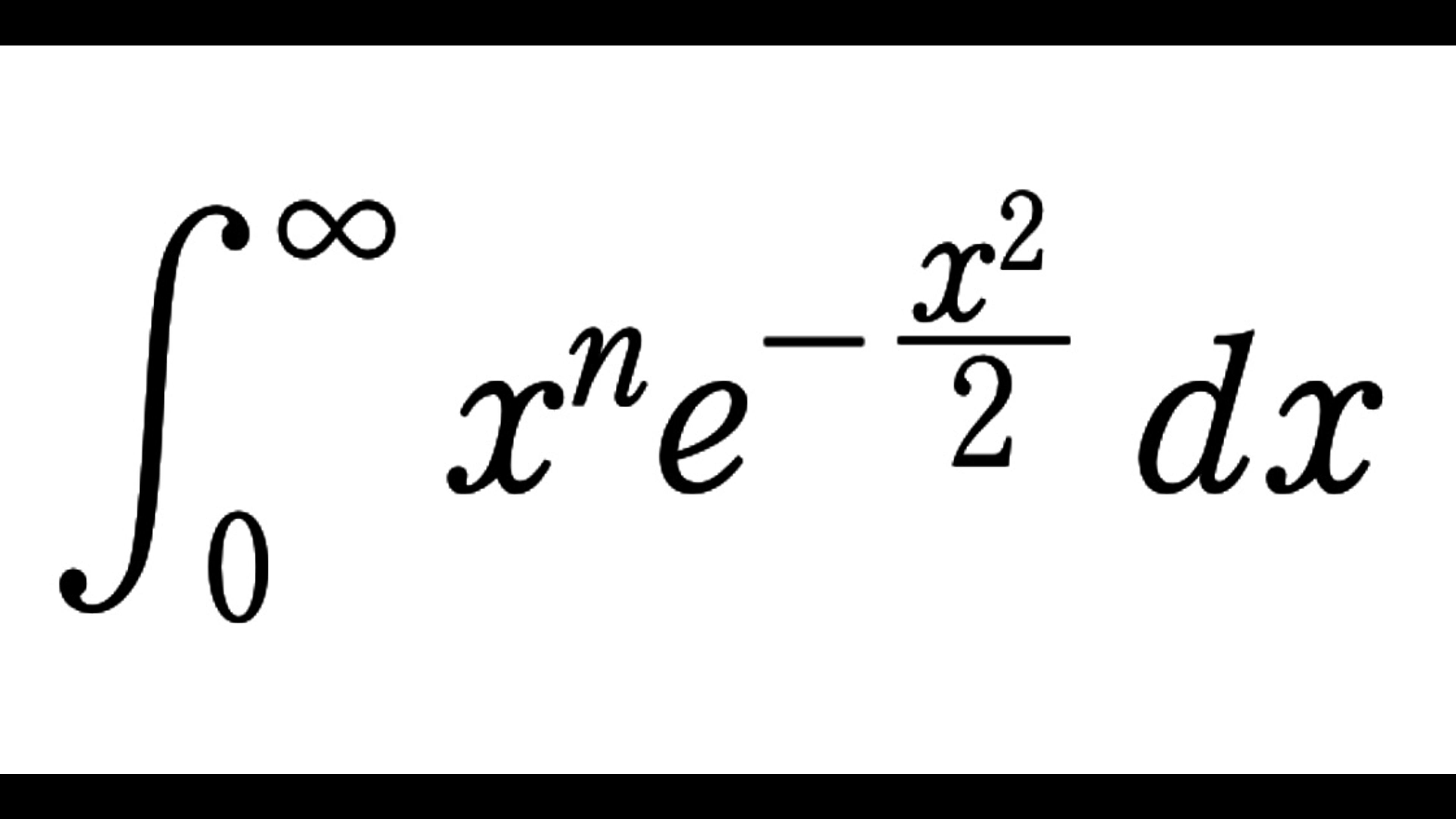

コメント