今回は「積分」の計算における部分分数分解のやり方を紹介したいと思います。
部分分数の和への計算では、恒等式の係数比較、具体的な数値の代入、裏ワザと呼ばれることのある ヘビサイドの展開定理 などの手法があります。本記事では、等式の証明ではなく計算途中の式変形を想定しているため、手法にはこだわらず柔軟に考えてゆきます。
私が意識している点を、一例として共有できればと思います。ただ手順を暗記するのではなく、頭を使って考え、手を動かしてゆきましょう!
練習問題 全12問

分数関数 \(f(x)\) の不定積分や定積分を求めてゆくわけですが、その \(f(x)\) を積分が具体的に計算できる形に変形しなければなりません。
分母が \(3\) 次以下の場合、例えば
\begin{align}
&\frac{1}{x-\alpha},&
&\frac{1}{(x-\alpha)^2},&
&\frac{1}{(x-\alpha)^3}
\end{align}
の形ならば、それぞれの原始関数として
\begin{align}
&\log|x-\alpha|,&
&-\frac{1}{x-\alpha},&
&-\frac{1}{2(x-\alpha)^2}
\end{align}
がとれます。
\(1\) 次の積に因数分解できない \(2\) 次式が分母にある場合は、それを平方完成して $$(x-p)^2+q$$ などとすることで計算を進めてゆきます。
以下、積分を具体的に計算できる形を作ること を目標にして、部分分数分解を行います。
思考の過程を明確にしながら以下の計算を行ってみましょう!
特に断りのない限り、\(C\) は積分定数を表すものとします。
分母が \((x-1)(x+2)\)
まずは、分母が \(1\) 次の積に因数分解可能な \(2\) 次式の場合です。
不定積分 \(\displaystyle \int \frac{1}{x^2+x-2}\,dx\) を求めよ。
分母を因数分解し、分解した後の分母を設定します。
\begin{align}
\int \frac{1}{x^2+x-2}\,dx
&=\int \frac{1}{(x-1)(x+2)}\,dx\\
&=\frac{1}{\fbox{?}}\int \left(\frac{\fbox{?}}{x-1}-\frac{\fbox{?}}{x+2}\right)\,dx
\end{align}
分母を同じ因数ごとに分離します。このとき、\(\fbox{?}\) の部分は空欄にしておき、後から書き加えるで良いと思います。先頭の分数に関しては、スペースを空けておいて分数ごと書かないでおいて良いでしょう。
右辺を通分したときに “とにかく分子から \(x\) を消去したい” と思います。定数であれば、先頭の分数を使っていくらでも調整可能です。
分母の \(x\) の係数は共に \(1\) ですから、そのまま差をとれば \(x\) の項は消えます。よって、分子は等しく \(1\) にできます。
\begin{align}
\int \frac{1}{x^2+x-2}\,dx
&=\frac{1}{\fbox{?}}\int \left(\frac{1}{x-1}-\frac{1}{x+2}\right)\,dx
\end{align}
この時点で通分したときの \(x\) の項は消えるので、もう気にする必要はありません。右辺の分子の定数項のみ計算すると \(2-(-1)=3\) ですから
\begin{align}
\int \frac{1}{x^2+x-2}\,dx
&=\frac{1}{3}\int \left(\frac{1}{x-1}-\frac{1}{x+2}\right)\,dx
\end{align}
となります。
部分分数分解はここまでで終了です。もう計算できます。部分分数によって積分が計算できる形になっているので
\begin{align}
\int \frac{1}{x^2+x-2}\,dx
&=\frac{1}{3}\int \left(\frac{1}{x-1}-\frac{1}{x+2}\right)\,dx\\
&=\frac{1}{3}\left(\log|x-1|-\log|x+2|\right)+C\\
&=\frac{1}{3}\log\left|\frac{x-1}{x+2}\right|+C
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{x}{x^2+x-2}\,dx\) を求めよ。
\begin{align}
\int \frac{x}{x^2+x-2}\,dx
&=\int \frac{x}{(x-1)(x+2)}\,dx\\
&=\frac{1}{\fbox{?}}\int \left(\frac{\fbox{?}}{x-1}-\frac{\fbox{?}}{x+2}\right)\,dx
\end{align}
ここまでは同様です。今回は、右辺を通分したときに “とにかく分子から定数項を消去したい” です。分母の定数項は \(-1\) と \(2\) なので、その比を \(1:(-2)\) と捉えると
\begin{align}
\int \frac{x}{x^2+x-2}\,dx
&=\frac{1}{\fbox{?}}\int \left(\frac{1}{x-1}-\frac{-2}{x+2}\right)\,dx\\
&=\frac{1}{\fbox{?}}\int \left(\frac{1}{x-1}+\frac{2}{x+2}\right)\,dx
\end{align}
とすることで定数項が消えます。
左辺の分子は \(x\) ですね。この比 \(1:(-2)\) とは、右辺に \(x=0\) を代入したときに被積分関数 \(=0\) となるような分子の比なのです。
この時点で通分したときの定数項は気にする必要がなく、右辺の分子の \(x\) の係数のみ計算すると \(1+2=3\) ですから
\begin{align}
\int \frac{x}{x^2+x-2}\,dx
&=\frac{1}{3}\int \left(\frac{1}{x-1}+\frac{2}{x+2}\right)\,dx
\end{align}
となります。
部分分数分解はここまでで終了です。もう計算できますね。部分分数によって積分が計算できる形になっているので
\begin{align}
\int \frac{x}{x^2+x-2}\,dx
&=\frac{1}{3}\int \left(\frac{1}{x-1}+\frac{2}{x+2}\right)\,dx\\
&=\frac{1}{3}\left(\log|x-1|+2\log|x+2|\right)+C\\
&=\frac{1}{3}\log|x-1|(x+2)^2+C
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{x+5}{x^2+x-2}\,dx\) を求めよ。
\begin{align}
\int \frac{x+5}{x^2+x-2}\,dx
&=\int \frac{x+5}{(x-1)(x+2)}\,dx\\
&=\frac{1}{\fbox{?}}\int \left(\frac{\fbox{?}}{x-1}-\frac{\fbox{?}}{x+2}\right)\,dx
\end{align}
今回は、右辺を通分したときに “とりあえず分子が \(x+5\) の定数倍になるようにしたい” と思いますので、右辺に \(x=-5\) を代入したときに被積分関数 \(=0\) となれば良いです。右辺の被積分関数に代入したとき
\begin{align}
\frac{\fbox{?}}{-6}-\frac{\fbox{?}}{-3}
\end{align}
これが \(0\) になるので、分子の比は \(2:1\) にすれば良く
\begin{align}
\int \frac{x+5}{x^2+x-2}\,dx
&=\frac{1}{\fbox{?}}\int \left(\frac{2}{x-1}-\frac{1}{x+2}\right)\,dx
\end{align}
とできます。この時点で、通分したときの \(x\) の係数と定数項の比は気にする必要がありません。例えば、\(1\) にしたい分子の \(x\) の係数のみ計算すると \(2-1=1\) ですから、分数は必要なく
\begin{align}
\int \frac{x+5}{x^2+x-2}\,dx
&=\int \left(\frac{2}{x-1}-\frac{1}{x+2}\right)\,dx
\end{align}
となります。
部分分数分解はここまでで終了です。積分の計算をすると
\begin{align}
\int \frac{x+5}{x^2+x-2}\,dx
&=\int \left(\frac{2}{x-1}-\frac{1}{x+2}\right)\,dx\\
&=2\log|x-1|-\log|x+2|+C\\
&=\log\frac{(x-1)^2}{|x+2|}+C
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{x^2}{x^2-1}\,dx\) を求めよ。(茨城大学)
分母が \((x-1)^2(x+2)\)
次に、分母を因数分解したとき \(2\) 乗を含む場合です。
不定積分 \(\displaystyle \int \frac{1}{x^3-3x+2}\,dx\) を求めよ。
分母を因数分解し、分解した後の分母を設定します。最初から一発ではゴールを目指さず、今までの経験を活かしつつも段階的に進めてゆきます。
今までと同様に、右辺を通分したときに “とにかく分子から定数項以外を消去したい” と思います。分母の最高次の係数は共に \(1\) ですから、はじめから \(x^2\) を消すことを意識して
\begin{align}
\int \frac{1}{x^3-3x+2}\,dx
&=\int \frac{1}{(x-1)^2(x+2)}\,dx\\
&=\frac{1}{\fbox{?}}\int \left\{\frac{x+\fbox{?}}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx
\end{align}
と設定できます。
次に、\(x\) の項を消去したいので、通分したときに現れる \((x+2)(x+\fbox{?})\) の \(x\) の係数が \((x-1)^2\) の \(x\) の係数 \(-2\) に等しければ良く
\begin{align}
\int \frac{1}{x^3-3x+2}\,dx
=\frac{1}{\fbox{?}}\int \left\{\frac{x-4}{(x-1)^2}-\frac{1}{x+2}\right\}dx
\end{align}
とできます。このとき、分子の定数項のみ計算すると $$(-4) \times 2-1 \times 1=-9$$ ですから
\begin{align}
\int \frac{1}{x^3-3x+2}\,dx
=-\frac{1}{9}\int \left\{\frac{x-4}{(x-1)^2}-\frac{1}{x+2}\right\}dx
\end{align}
となります。
部分分数分解はここまでで一旦終了です。積分の計算をするためには $$x-4=(x-1)-3$$ であることを用いて
\begin{align}
\int \frac{1}{x^3-3x+2}\,dx
&=-\frac{1}{9}\int \left\{\frac{x-4}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=-\frac{1}{9}\int \left\{\frac{(x-1)-3}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=-\frac{1}{9}\int \left\{\frac{1}{x-1}-\frac{3}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=-\frac{1}{9}\left(\log|x-1|+\frac{3}{x-1}-\log|x+2|\right)+C\\
&=\frac{1}{9}\log\left|\frac{x+2}{x-1}\right|-\frac{1}{3(x-1)}+C
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{x-7}{x^3-3x+2}\,dx\) を求めよ。
こちらも同様に、右辺を通分したとき、はじめから \(x^2\) を消すことを意識して
\begin{align}
\int \frac{x-7}{x^3-3x+2}\,dx
&=\int \frac{x-7}{(x-1)^2(x+2)}\,dx\\
&=\frac{1}{\fbox{?}}\int \left\{\frac{x+\fbox{?}}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx
\end{align}
と設定します。
次に、もとの分子が \(x-7\) なので、右辺の被積分関数において \(x=7\) とすると $$\frac{7+\fbox{?}}{6^2}-\frac{1}{9}=0$$ すなわち $$7+\fbox{?}=4$$ なので \(\fbox{?}=-3\) となります。
\begin{align}
\int \frac{x-7}{x^3-3x+2}\,dx
=\frac{1}{\fbox{?}}\int \left\{\frac{x-3}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx
\end{align}
と設定できます。
この時点で通分したときの分子は \(x-7\) 定数倍となり、分子の \(x\) の係数のみ計算すると $$(-1)-(-2)=1$$ ですから、そのまま
\begin{align}
\int \frac{x-7}{x^3-3x+2}\,dx
=\int \left\{\frac{x-3}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx
\end{align}
となります。
部分分数分解はここまでで一旦終了です。積分の計算をするためには $$x-3=(x-1)-2$$ であることを用いて
\begin{align}
\int \frac{x-7}{x^3-3x+2}\,dx
&=\int \left\{\frac{x-3}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=\int \left\{\frac{(x-1)-2}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=\int \left\{\frac{1}{x-1}-\frac{2}{(x-1)^2}-\frac{1}{x+2}\right\}\,dx\\
&=\log|x-1|+\frac{2}{x-1}-\log|x+2|+C\\
&=\log\left|\frac{x-1}{x+2}\right|+\frac{2}{x-1}+C
\end{align}
となります。
分母が \(x^3+1\)
次は、実数の範囲で因数分解できない因数が分母に含まれる場合です。
定積分 \(\displaystyle \int_0^1 \frac{1}{x^3+1}\,dx\) を求めよ。
しつこいですが、右辺を通分したときに “とにかく分子から定数項以外を消去したい” と思います。\(x^2\) の係数と \(x\) の係数から
\begin{align}
\int_0^1 \frac{1}{x^3+1} dx
&=\int_0^1 \frac{1}{(x+1)(x^2-x+1)} dx\\
&=\frac{1}{\fbox{?}}\int_0^1 \left(\frac{1}{x+1}-\frac{x+\fbox{?}}{x^2-x+1}\right)dx\\
&=\frac{1}{\fbox{?}}\int_0^1 \left(\frac{1}{x+1}-\frac{x-2}{x^2-x+1}\right)dx
\end{align}
と設定できます。この時点で通分したときの分子から定数項以外が消え去ります。
このとき、分子の定数項のみ計算すると $$1 \times 1-(-2) \times 1=3$$ ですから
\begin{align}
\int \frac{1}{x^3+1} dx
&=\frac{1}{3}\int_0^1 \left(\frac{1}{x+1}-\frac{x-2}{x^2-x+1}\right)dx
\end{align}
となります。
積分を実際に計算するためには、$$(x^2-x+1)^\prime=2x-1$$ より
\begin{align}
\int_0^1 \frac{1}{x^3+1} dx
&=\frac{1}{3}\int_0^1 \left(\frac{1}{x+1}-\frac{x-2}{x^2-x+1}\right)dx\\
&=\frac{1}{3}\int_0^1 \left\{\frac{1}{x+1}-\frac{1}{2}\frac{(2x-1)-3}{x^2-x+1}\right\}dx\\
&=\frac{1}{3}\int_0^1 \left(\frac{1}{x+1}-\frac{1}{2}\frac{2x-1}{x^2-x+1}-\frac{3}{2}\frac{1}{x^2-x+1}\right)dx
\end{align}
として処理をします。
第一項について
\begin{align}
\int_0^1 \frac{1}{x+1}dx=[\log|x+1|]_0^1=\log2
\end{align}
第二項について
\begin{align}
\frac{1}{2}\int_0^1 \frac{2x-1}{x^2-x+1}dx=\frac{1}{2}[\log(x^2-x+1)]_0^1=0
\end{align}
第三項について、\(\displaystyle \frac{2x-1}{\sqrt{3}}=\tan\theta\) とおくと
\begin{align}
\frac{3}{2}\int_0^1 \frac{1}{x^2-x+1} dx
&=2\int_0^1 \frac{1}{\left(\frac{2x-1}{\sqrt{3}}\right)^2+1} dx\\
&=2\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \frac{1}{\tan^2\theta+1}\frac{\sqrt{3}}{2}\frac{1}{\cos^2\theta}d\theta\\
&=\sqrt{3}\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}d\theta\\
&=\sqrt{3}\left\{\frac{\pi}{6}-\left(-\frac{\pi}{6}\right)\right\}\\
&=\frac{\pi}{\sqrt{3}}
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{x-1}{x^3+1}\,dx\) を求めよ。
右辺を通分したときに “まず分子から \(x^2\) の項を消去したい” です。
\begin{align}
\int \frac{x-1}{x^3+1} dx
&=\int \frac{x-1}{(x+1)(x^2-x+1)} dx\\
&=\frac{1}{\fbox{?}}\int \left(\frac{1}{x+1}-\frac{x+\fbox{?}}{x^2-x+1}\right)dx
\end{align}
と設定できます。
右辺の被積分関数に \(x=1\) を代入すると \(0\) となる必要があるので $$\frac{1}{2}-\frac{1+\fbox{?}}{1}=0$$ より \(\displaystyle \fbox{?}=-\frac{1}{2}\) となります。
このとき、先頭の分数を加味して被積分関数を \(2\) 倍すると
\begin{align}
\int \frac{x-1}{x^3+1} dx
&=\frac{1}{\fbox{?}}\int \left(\frac{2}{x+1}-\frac{2x-1}{x^2-x+1}\right)dx
\end{align}
となります。
分子の定数項のみ計算すると $$2 \times 1-(-1) \times 1=3$$ ですから
\begin{align}
\int \frac{x-1}{x^3+1} dx
&=-\frac{1}{3}\int \left(\frac{2}{x+1}-\frac{2x-1}{x^2-x+1}\right)dx
\end{align}
となります。
積分を実際に計算すると
\begin{align}
\int \frac{x-1}{x^3+1} dx
&=-\frac{1}{3}\int \left(\frac{2}{x+1}-\frac{2x-1}{x^2-x+1}\right)dx\\
&=-\frac{1}{3}\left\{2\log|x+1|-\log(x^2-x+1)\right\}+C\\
&=-\frac{1}{3}\log\frac{(x+1)^2}{x^2-x+1}+C
\end{align}
となります。
不定積分 \(\displaystyle \int \frac{4x^2+x+1}{x^3-1}\,dx\) を求めよ。(芝浦工業大学)
分母が \(x^4+1\)
最後に、分母が \(4\) 次式であるものをひとつ扱います。これに関しては積分ではなく、純粋に部分分数分解のみ行います。
\(\displaystyle \frac{1}{x^4+1}\) を部分分数分解せよ。
まず、
\begin{align}
\frac{1}{x^4+1}
&=\frac{1}{(x^2-\sqrt{2}x+1)(x^2+\sqrt{2}x+1)}
\end{align}
となります。
ここで、\(x^2\) の係数と \(x\) の係数の符号を変え、次数を調整したものを考えると
- \((x+\sqrt{2})(x^2-\sqrt{2}x+1)=x^3-x+\sqrt{2}\)
- \((x-\sqrt{2})(x^2+\sqrt{2}x+1)=x^3-x-\sqrt{2}\)
これらの差をとれば良いので
\begin{align}
\frac{1}{x^4+1}
=-\frac{1}{2\sqrt{2}}\left(\frac{x-\sqrt{2}}{x^2-\sqrt{2}x+1}-\frac{x+\sqrt{2}}{x^2+\sqrt{2}x+1}\right)
\end{align}
となります。
\(\displaystyle \frac{x}{x^4+1}\) を部分分数分解せよ。
まず、
\begin{align}
\frac{x}{x^4+1}
&=\frac{x}{(x^2-\sqrt{2}x+1)(x^2+\sqrt{2}x+1)}
\end{align}
となります。分母にある因数の差が、分子にある \(x\) の定数倍 \(2\sqrt{2}x\) になるので
\begin{align}
\frac{x}{x^4+1}
=\frac{1}{2\sqrt{2}}\left(\frac{1}{x^2-\sqrt{2}x+1}-\frac{1}{x^2+\sqrt{2}x+1}\right)
\end{align}
となります。
今、部分分数分解した \(\displaystyle \frac{x}{x^4+1}\) の定積分 $$\int_0^1\frac{x}{x^4+1}\,dx$$ を求めるときは、上記の部分分数分解を用いるのが最善の手でしょうか?
例えば、\(x^2=\tan\theta\) とおくと \(\displaystyle 2xdx=\frac{1}{\cos^2\theta}d\theta\) なので
\begin{align}
\int_0^1\frac{x}{x^4+1}\,dx
&=\int_0^{\frac{\pi}{4}}\frac{1}{\tan^2\theta+1}\frac{1}{2\cos^2\theta}\,d\theta\\
&=\frac{1}{2}\int_0^{\frac{\pi}{4}}\,d\theta\\
&=\frac{\pi}{8}
\end{align}
と求まります。
冒頭の問題を解く!
さて、この記事のアイキャッチにもなっている積分の計算をしてみましょう!
不定積分 \(\displaystyle \int \frac{1}{x(x+1)^2}\,dx\) を求めよ。
\begin{align}
\int \frac{1}{x(x+1)^2}\,dx
&=\frac{1}{\fbox{?}}\int \left\{\frac{1}{x}-\frac{x+\fbox{?}}{(x+1)^2}\right\}\,dx
\end{align}
通分したときに分子に現れる \((x+1)^2\) の \(x\) の係数は \(2\) なので
\begin{align}
\int \frac{1}{x(x+1)^2}\,dx
&=\frac{1}{\fbox{?}}\int \left\{\frac{1}{x}-\frac{x+2}{(x+1)^2}\right\}\,dx
\end{align}
通分したときに分子に現れる定数項は \(1\) なので
\begin{align}
\int \frac{1}{x(x+1)^2}\,dx
&=\int \left\{\frac{1}{x}-\frac{x+2}{(x+1)^2}\right\}\,dx
\end{align}
ここまでを一行で計算するので、以下のように解答が進みます。ここで、\(x+2=(x+1)+1\) に注意します。
\begin{align}
\int \frac{1}{x(x+1)^2}\,dx
&=\int \left\{\frac{1}{x}-\frac{x+2}{(x+1)^2}\right\}\,dx\\
&=\int \left\{\frac{1}{x}-\frac{1}{x+1}-\frac{1}{(x+1)^2}\right\}\,dx\\
&=\log|x|-\log|x+1|+\frac{1}{x+1}+C\\
&=\log\left|\frac{x}{x+1}\right|+\frac{1}{x+1}+C
\end{align}
これが答えです。
数列の和について
今回は、部分分数分解がよく扱われるテーマのうち「積分の計算」について考えてきました。
もう一つのテーマである「数列の和」に関しては、以下の記事 をご覧ください
今回、積分の計算をすること を目標にしたために分解の自由度が高かったですが、隣接する項の差を作ること を目標とすることで形が限定されます。階差を利用して計算が進む様子を、なぜそうなるのかまで説明してゆきます。
部分分数分解の理論については以下の関連記事をご覧ください。
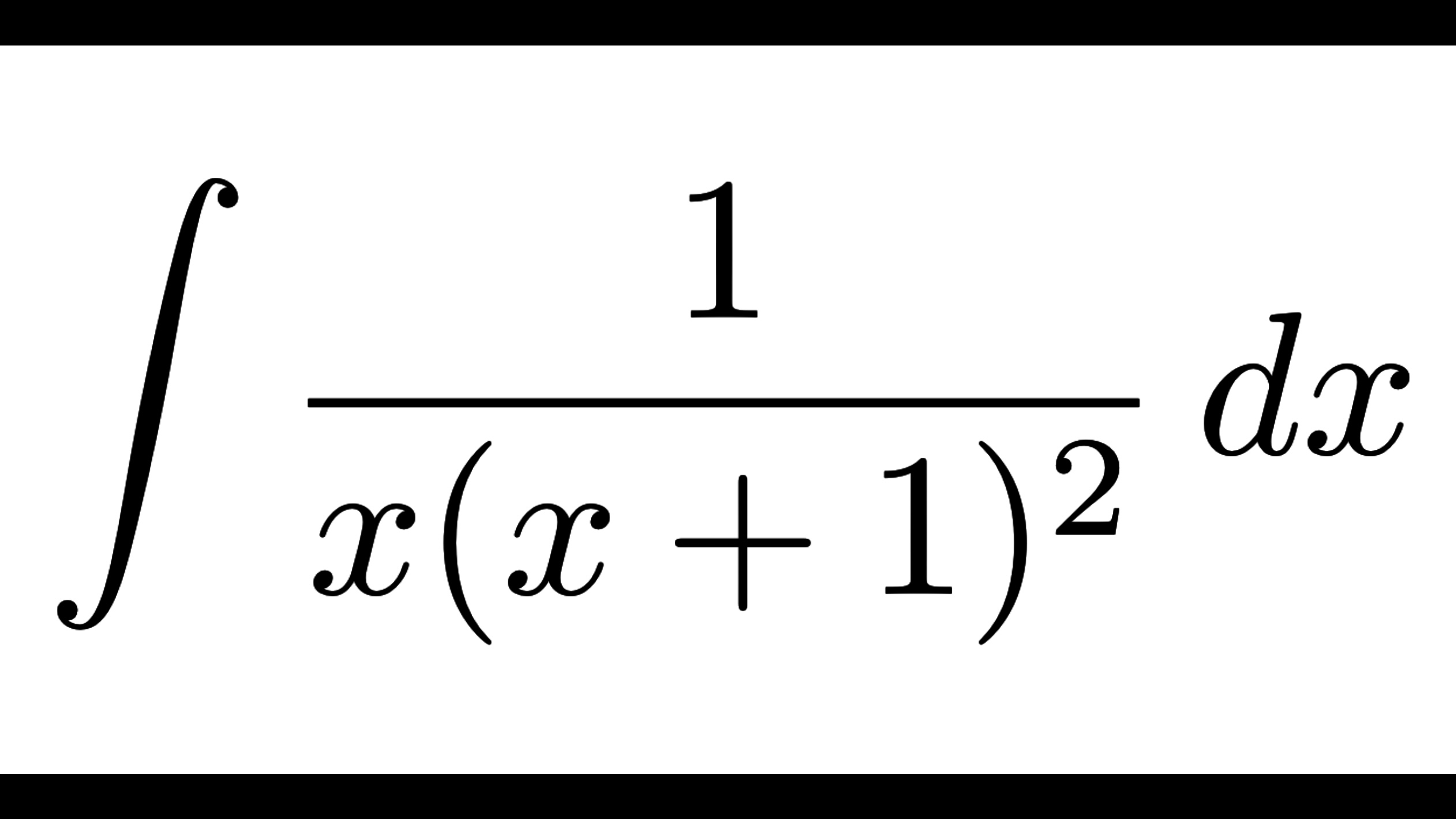
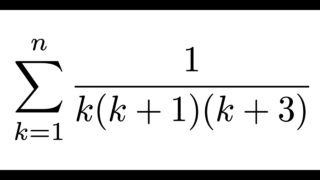
コメント