みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(n\) に対して、次の定積分
\begin{align}
L_n&=\int_1^e (\log x)^n\,dx
\end{align}
を考える。但し、\((\log x)^0=1\) とする。
(1)\(L_0\) を求めよ。
(2)\(n\geq1\) に対して \(L_n\) を \(L_{n-1}\) で表すことで \(L_5\) を求めよ。
その他の例題は以下のリンクを参照してください。
答え
(1)\(\displaystyle L_0=e-1\)
(2)\(\displaystyle L_5=120-44e\)
解説

\(L_0\) を求める。
まず、\((\log x)^0=1\) と約束していたので
\begin{align}
L_0
=\int_1^e 1\,dx
=e-1
\end{align}となります。
\(L_n\) の漸化式を求める。
\(n\geq1\) であることを用いて部分積分を行います。
\begin{align}
L_n
&=\int_1^e (\log x)^n\,dx\\
&=\left[x(\log x)^n\right]_1^e-\int_1^e x\times \left\{\frac{n}{x}(\log x)^{n-1}\right\}\,dx\\
&=e-n\int_1^e (\log x)^{n-1}\,dx\\
&=e-n L_{n-1}
\end{align}
を得ます。
漸化式を繰り返し用いることで、順に
\begin{align}
L_1
&=e-L_0\\
&=e-(e-1)\\
&=1
\end{align}
\begin{align}
L_2
&=e-2L_1\\
&=e-2
\end{align}
\begin{align}
L_3
&=e-3L_2\\
&=e-3(e-2)\\
&=6-e
\end{align}
\begin{align}
L_4
&=e-4L_3\\
&=e-4(6-e)\\
&=9e-24
\end{align}
\begin{align}
L_5
&=e-5L_4\\
&=e-5(9e-24)\\
&=120-44e
\end{align}
となります。
最後に

さて、数列 \(\{L_n\}\) の 一般項 が明示的に書けるか考えてみましょう。
漸化式 \(L_n=e-n L_{n-1}\) より
\begin{align}
\frac{(-1)^n}{n!}L_n=\frac{(-1)^{n-1}}{(n-1)!}L_{n-1}+e\frac{(-1)^n}{n!}
\end{align}
よって、\(n\geq1\) について
\begin{align}
\frac{(-1)^n}{n!}L_n
&=\frac{(-1)^0}{0!}L_0+e\sum_{k=1}^n\frac{(-1)^k}{k!}\\
&=(e-1)+e\sum_{k=1}^n\frac{(-1)^k}{k!}\\
&=e\sum_{k=0}^n\frac{(-1)^k}{k!}-1
\end{align}となり、これは \(n=0\) のときも成り立ちます。
これより、任意の非負整数 \(n\) に対して
\begin{align}
L_n
&=(-1)^nn!\left\{e\sum_{k=0}^n\frac{(-1)^k}{k!}-1\right\}
\end{align}と書くことができます。
関連 : 数学IIICカテゴリー
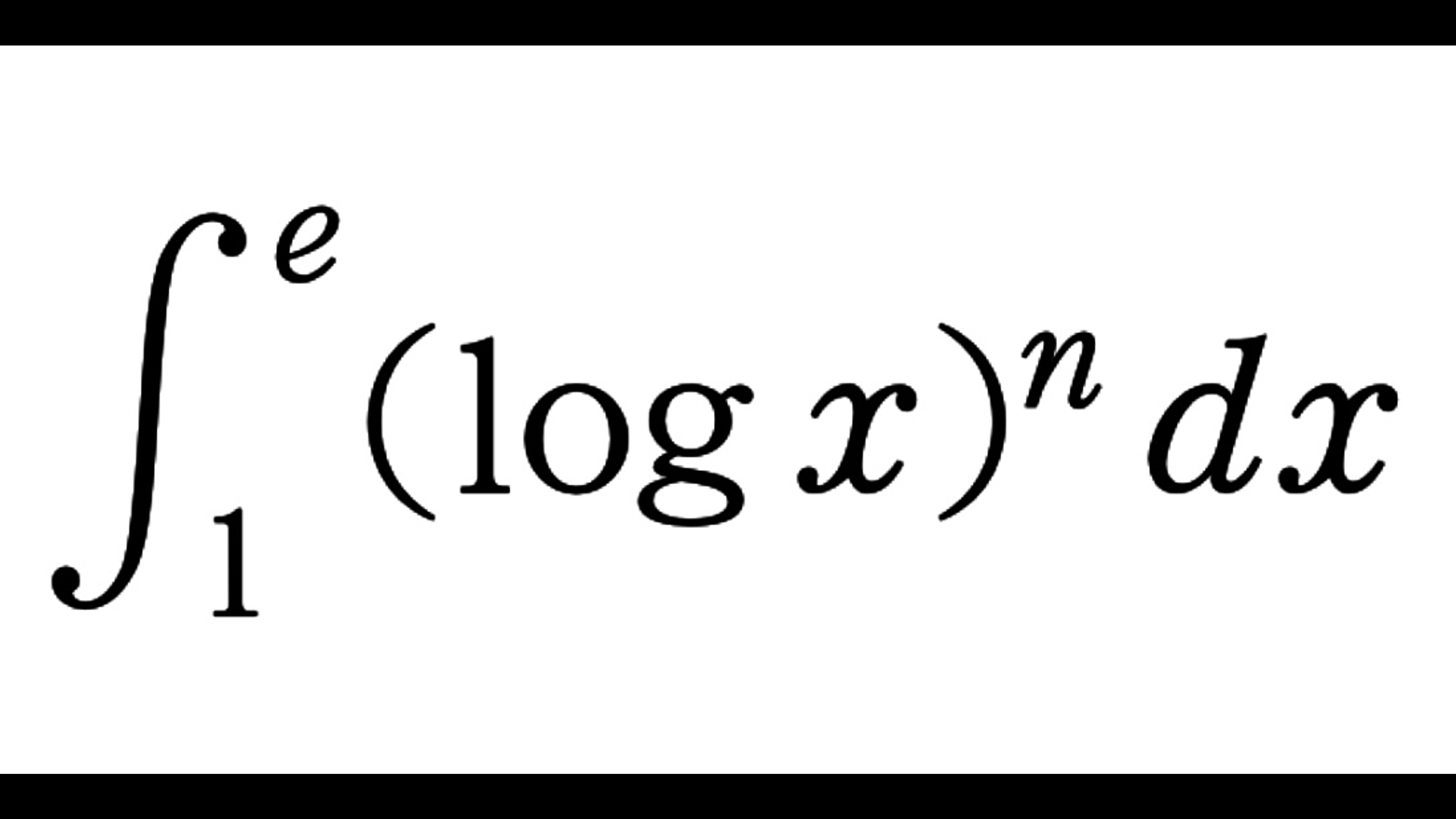

コメント