みなさん、こんにちは。
今回は、次の問題を解いてゆきます。
\(0\) 以上の整数 \(m\),\(n\) に対して、次の定積分
\begin{align}
I_{m,n}&=\int_0^{\frac{\pi}{2}} \sin^m x\cos^n x\,dx
\end{align}
を考える。但し、\(\sin^0 x\),\(\cos^0 x\) は共に \(1\) とする。
(1)\(I_{m,0}\) と \(I_{m,1}\) を求めよ。
(2)\(n\geq2\) とする。部分積分によって $$I_{m,n}=\frac{n-1}{m+n}I_{m,n-2}$$ を示せ。
(3)\(I_{m,n}\) を求めよ。
この記事は、ウォリス積分 に関する 記事 で紹介した二重階乗による表示を前提としています。設定によっては高校範囲の問題にアレンジ可能ですが、今回は 高校数学+α として扱います。
その他の例題は以下のリンクを参照してください。
答え
(1)
\begin{align}
I_{m,0}&=\begin{cases}
\displaystyle \frac{(m-1)!!}{m!!}\times\frac{\pi}{2}&(m:偶数)\\[5pt]
\displaystyle \frac{(m-1)!!}{m!!}&(m:奇数)
\end{cases}
\end{align}
また
\begin{align}
I_{m,1}&=\frac{1}{m+1}
\end{align}
(2)省略。
(3)\(m\) と \(n\) が共に偶数のとき
\begin{align}
I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}\times\frac{\pi}{2}
\end{align}
その他の場合
\begin{align}
I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}
\end{align}
解説

\(I_{m,0}\) と \(I_{m,1}\) を求める。
まず、\(\cos^0 x=1\) と約束していたので、ウォリス積分より
\begin{align}
I_{m,0}
&=\int_0^{\frac{\pi}{2}} \sin^m x\,dx\\[5pt]
&=\begin{cases}
\displaystyle \frac{(m-1)!!}{m!!}\times\frac{\pi}{2}&(m:偶数)\\[5pt]
\displaystyle \frac{(m-1)!!}{m!!}&(m:奇数)
\end{cases}
\end{align}
となります。
また、
\begin{align}
I_{m,1}
&=\int_0^{\frac{\pi}{2}} \sin^m x\cos x\,dx\\
&=\left[\frac{1}{m+1}\sin^{m+1} x\right]_0^{\frac{\pi}{2}}\\
&=\frac{1}{m+1}
\end{align}
となります。
\(I_{m,n}\) の漸化式を求める。
\(n\geq2\) であることを用いて部分積分を行います。
\begin{align}
I_{m,n}
&=\int_0^{\frac{\pi}{2}}(\sin^m x\cos x)\cos^{n-1} x\,dx\\
&=\left[\frac{1}{m+1}\sin^{m+1} x\times\cos^{n-1} x\right]_0^{\frac{\pi}{2}}\\
&\quad-\int_0^{\frac{\pi}{2}} \frac{1}{m+1}\sin^{m+1} x(n-1)(-\sin x)\cos^{n-2} x\,dx\\
&=0+\frac{n-1}{m+1}\int_0^1 \sin^m x(\sin^2 x)\cos^{n-2} x \,dx\\
&=\frac{n-1}{m+1}\int_0^1 \sin^m x(1-\cos^2 x)\cos^{n-2} x \,dx\\
&=\frac{n-1}{m+1}(I_{m,n-2}-I_{m,n})
\end{align}
これを \(I_{m,n}\) について解くことで
\begin{align}
I_{m,n}=\frac{n-1}{m+n}I_{m,n-2}
\end{align}を得ます。
\(I_{m,n}\) を求める。
\(n\) が偶数のとき
\(n\geq2\) とすると、(2)より
\begin{align}
I_{m,n}
&=\frac{n-1}{m+n}\times I_{m,n-2}\\
&=\frac{n-1}{m+n}\times \frac{n-3}{m+n-2}\times I_{m,n-4}\\
&\quad\qquad\vdots\\
&=\frac{n-1}{m+n}\times \frac{n-3}{m+n-2}\times\cdots\times\frac{1}{m+2}\times I_{m,0}\\
&=\frac{m!!(n-1)!!}{(m+n)!!}\times I_{m,0}
\end{align}
となります。よって、(1)より
\begin{align}
I_{m,n}
&=\begin{cases}
\displaystyle \frac{(m-1)!!(n-1)!!}{(m+n)!!}\times\frac{\pi}{2}&(m:偶数)\\[5pt]
\displaystyle \frac{(m-1)!!(n-1)!!}{(m+n)!!}&(m:奇数)
\end{cases}
\end{align}
となります。
これは、(1)より \(n=0\) のときも成り立ちます。
\(n\) が奇数のとき
\(n\geq2\) とすると、(2)より
\begin{align}
I_{m,n}
&=\frac{n-1}{m+n}\times I_{m,n-2}\\
&=\frac{n-1}{m+n}\times \frac{n-3}{m+n-2}\times I_{m,n-4}\\
&\quad\qquad\vdots\\
&=\frac{n-1}{m+n}\times \frac{n-3}{m+n-2}\times\cdots\times\frac{2}{m+3}\times I_{m,1}\\
&=\frac{(m+1)!!(n-1)!!}{(m+n)!!}\times I_{m,1}
\end{align}
となります。よって、(1)より
\begin{align}
I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}
\end{align}
となります。
これは、(1)より \(n=1\) のときも成り立ちます。
まとめると
\(m\) と \(n\) が共に偶数のときは
\begin{align}
I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}\times\frac{\pi}{2}
\end{align}
となります。また、その他の場合は
\begin{align}
I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}
\end{align}
となります。
最後に

今回導いた公式を用いて具体的な計算をしてみましょう。
\begin{align}
I_{6,4}
&=\frac{5!!\times3!!}{10!!}\times\frac{\pi}{2}
=\frac{3}{512}\pi
\end{align}
また
\begin{align}
I_{5,3}
&=\frac{4!!\times2!!}{8!!}
=\frac{1}{24}
\end{align}
となります。
また、この公式の基づいて \(I_{2m-1,2n-1}\) を計算すると
\begin{align}
I_{2m-1,2n-1}
&=\frac{(2m-2)!!(2n-2)!!}{(2m+2n-2)!!}\\
&=\frac{2^{m-1}(m-1)!\times 2^{n-1}(n-1)!}{2^{m+n-1}(m+n-1)!}\\
&=\frac{(m-1)!(n-1)!}{2(m+n-1)!}\\
&=\frac{1}{2}B(m,n)
\end{align}
を得ます。
但し、$$B(m,n)=\int_0^1 x^{n-1}(1-x)^{m-1} dx$$ (ベータ関数)です。詳しくは以下の記事を参考にしてください。
関連 : 数学IIICカテゴリー
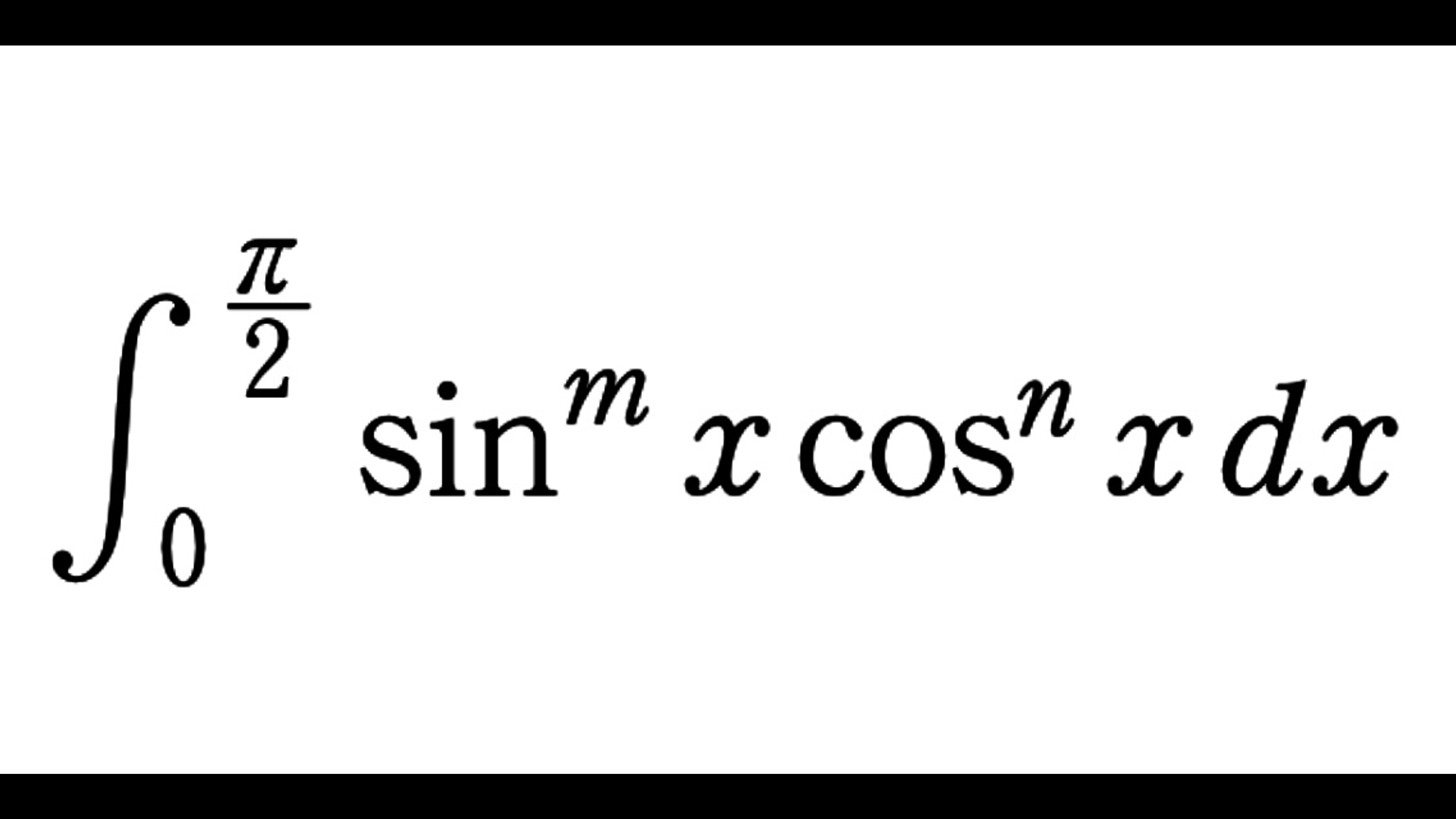
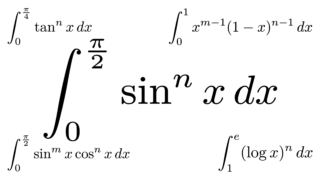
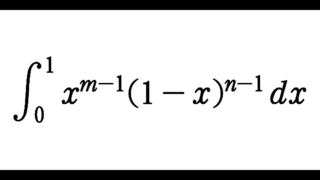

コメント